推力槽形凸轮零件的数控加工工艺及数值处理
王 鑫,郭建烨,于 超
(1.三一重型装备有限公司,辽宁 沈阳 110027;2.沈阳航空航天大学机电工程学院,辽宁 沈阳 110136)
数控加工在现代机械制造业中已经被广泛应用。数控程序的编制是数控加工中的主要工作,程序编制的结果就是将加工过程中刀具的轨迹、工艺参数等信息用数控系统所能识别的代码来表示,程序编制得正确与否将直接影响着数控加工的质量。其中,数控加工的工艺及数值处理是程序编制的关键,合理的处理过程和结果是保证获得正确数控程序的基础[1-2]。本文以一种双面推力槽形凸轮为研究对象,重点分析了该零件在进行数控加工时的工艺及数值处理过程,基于处理结果所编制出来的数控加工程序完全可以应用于该零件的实际生产。
1 凸轮零件的设计结构
本论文所研究的推力槽形凸轮属于双面结构,它为油田采油设备上的专用零件,其材料为灰铸铁HT300,该零件的生产类型为小批量生产。凸轮零件的具体结构如图1所示。本文主要研究该凸轮零件在数控铣削凹槽时的工艺及数值处理过程,所以在进行数控加工之前,零件的其它表面均已加工完毕。
2 数控加工的工艺处理
数控加工工艺处理是编制数控程序首要解决的问题,它也是编制数控程序的依据。无论是采用手工编程方式还是自动编程方式,编程工作都要从工艺处理开始。工艺处理过程是否合理,将直接影响到数控加工质量、生产效率及加工成本[3]。在加工本文所研究的凸轮凹槽时,选择在配有FANUC 0i-MA控制系统的VMC-1000立式加工中心上进行。下面就以加工第一面凹槽曲线轮廓为例,说明工艺处理过程主要完成的几方面工作。
2.1 工件的安装
由于数控机床是按照程序自动加工零件的,在机床空间内刀具与零件之间总是存在一定的位置关系。为了保证二者处于正确的位置,要求每一个工件在夹具上的装夹必须精确定位,加工中不允许变形,而且力求减少工件的装卸时间[4]。根据数控加工的特点及对工件安装的要求,确定此凸轮零件加工中采用专用夹具安装工件,以第二面、孔Φ35+0.025mm(H7)和键槽作为定位基准,并采用开口垫圈配合螺母夹紧的方式。
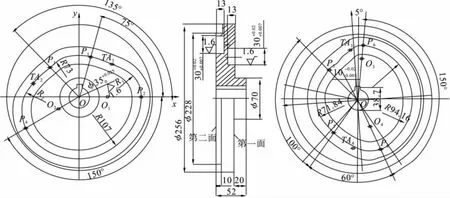
图1 推力槽形凸轮零件图
2.2 建立加工坐标系
在建立加工坐标系时,主要考虑加工坐标系原点尽量与设计基准重合,这样便于进行数值计算[3]。由零件图可知,孔 Φ35+0.025 mm 的中心为凹槽曲线的设计基准,故将工件坐标系原点O(X0,Y0,Z0)选在孔 Φ35+0.025mm 的中心线与凸轮第一面的交点处。这样,可以根据夹具上的圆柱销和定位平面,很容易找出加工坐标系原点在机床坐标系中的坐标值,然后将该值用MDI方式输入到G55对应的偏置寄存器中,在程序中直接调用G55命令即可建立该加工坐标系。
2.3 确定刀具及工艺参数
数控加工对刀具材料的硬度与耐磨性、强度与韧性、耐热性等方面有较高要求,应根据工件材料的切削加工性、粗精加工要求及冲击振动与热处理等工况合理选用加工刀具。另外,还应合理选用切削用量及断屑槽形状与尺寸等以保证零件的加工质量[5]。
结合凸轮零件的实际情况,在加工中选用两把Φ25mm六刃高速钢立铣刀,分别用于粗加工、半精加工(T3)和精加工(T4)。为了保证顺利加工出所要求的凹槽深度,先用Φ25mm钻头(T1)钻出底孔,然后再用Φ25mm的键槽铣刀(T2)将孔底铣平。在进行粗加工(开槽)时分两次走刀完成,以避免Z向吃刀过深;而在进行半精加工和精加工时一次走刀完成。粗加工与半精加工过程中可不必区分逆铣和顺铣方式,但是为保证表面质量在精加工过程中要采用顺铣方式。具体的刀具选择及工艺参数如表1所示。
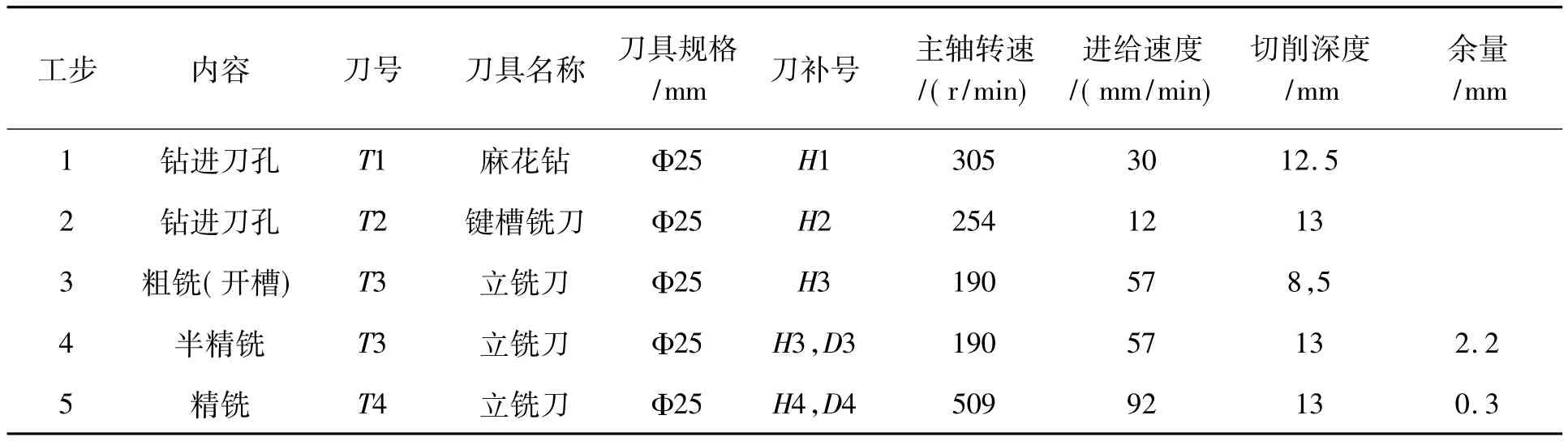
表1 刀具选择及工艺参数
2.4 确定走刀路线
走刀路线是指数控加工过程中刀位点相对于被加工工件的运动轨迹。走刀路线包括切削加工的路径及刀具引入、返回等非切削空行程。确定走刀路线时,首先要考虑保证加工质量,其次要使数值计算简单,另外就是要使走刀路线尽量短[3,6-7]。
结合零件结构图1,编程轨迹为凹槽的中心线轨迹,凹槽的内外侧表面可通过设置刀具半径补偿的形式加工出来,这样可以大大提高编程效率并简化编程过程。需要注意的是,本论文中所采用的机床只有在快进(G00)或直线进给(G01)过程中才能建立或撤销刀补。在粗加工和半精加工过程中,钻头(T1)和键槽铣刀(T2)在P1点处加工出预制孔,然后立铣刀(T3)从此处下刀开始加工。根据表1确定的工艺参数,在进行刀具半径左补偿和右补偿时,补偿量都选为2.2 mm,并都为精加工留0.3 mm余量;在精加工过程中,为保证表面质量都采用顺铣的加工方式。根据前面工序加工的半径补偿量及加工余量值,此过程中的半径补偿量都选为2.5 mm。另外,为了避免在工件表面上留下刀具转接痕迹,在刀具对凹槽铣削一周后要多走一段距离再离开加工表面。具体的走刀路线及加工过程如表2所示。

表2 走刀路线具体规划
3 数控加工的数值处理
数控加工中数值处理的目的是计算出编制程序时要输入的刀具加工轨迹坐标值。本论文所研究的凸轮凹槽轮廓是由直线和圆弧直接构成的曲线,插补过程中不涉及曲线的拟合,所以数值处理的主要任务就是计算出各个基点的坐标值[8-9]。
对于本凸轮的凹槽加工轨迹,需要计算坐标值的基点为 P1、P2、P3、PV4、TA1和 TA2,并且需计算过渡圆弧圆心O1和 O2的坐标值,而数值处理的关键就是计算出TA1、TA2、O1和 O2的坐标值。现将求解TA1和O1的坐标值及其过渡圆弧半径值R1的计算过程介绍如下,依据此过程同样可以求得TA2和O2的坐标值。
首先根据凸轮零件结构图对加工轨迹进行轮廓分析。可以看到,圆弧P2P4的半径为107 mm,圆弧P1P3的半径为73 mm,它们的圆心坐标都为O(X0,Y0);直线 P1TA1与圆弧 P1P3相切于 P1点,过渡圆弧P2TA1与圆弧P2P4相切于P2点,并与直线P1TA1相切于TA1点;同样,直线P3TA2与圆弧P1P3相切于P3点,过渡圆弧P4TA2与圆弧P2P4相切于P4点,并与直线P3TA2相切于TA2点。因此,所加工的轮廓曲线是由四段圆弧和两段直线构成的。
设r1与α1分别为P1点的极径和极角,r2与α2分别为 P2点的极径和极角,则P1(X1,Y1)和P2(X2,Y2)的坐标值分别为:

由于直线OP1的斜率为:k=Y1/X1,则与之垂直的切线P1TA1斜率为:k1=-X1/Y1,该切线的方程可表示为:
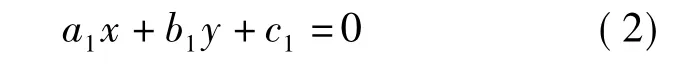
式中:a1=k1;b1= -1;c1=Y1-k1X1。
设O1点的坐标为(x0,y0),由于线段O1TA1垂直于线段P1TA1,且线段O1TA1的长度等于线段O1P2的长度,所以有下式成立:
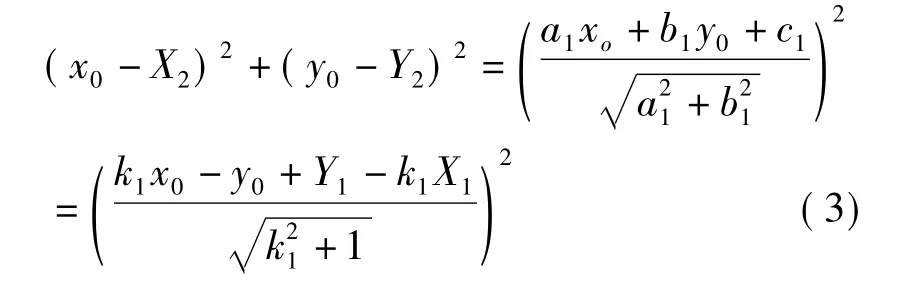
又因为O1点在直线OP2上,设直线OP2的斜率为k2,则有下式成立:

根据式(3)与式(4)即可解得O1点的坐标值(x0,y0)。
另外,直线O1TA1与直线OP1平行,则直线O1TA1的方程可表示为:

式中,b=y0-kx0。
根据式(2)与式(5)可得TA1点的坐标值(x1,y1),从而计算出过渡圆弧半径R1。同理可计算出其它圆心和切点的坐标值。在实际的数值处理中是通过编制一个专用程序来完成计算过程的,输入值分别为 P1点的极径 r1和极角 α1、P2点的极径r2和极角α2,计算结果为过渡圆弧圆心坐标值和切点(过渡圆弧起点)坐标值。其程序界面如图2所示[10],计算结果如表3所示。

表1 第一面各基点的坐标值
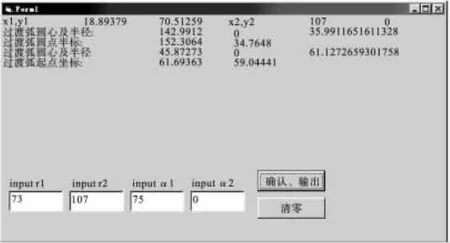
图2 数值处理计算程序界面
4 数控程序的编制
根据已确定的加工步骤、走刀路线以及数值处理结果,按数控指令要求即可编制出数控加工程序。另外,由于加工过程中刀具在水平面内沿编程轨迹要反复走刀,所以为了简化编程并考虑到精加工时的顺铣要求,可编制两个子程序供主程序调用。第一个子程序为顺圆子程序,刀具路径可规划为:TA1→P2→P4→TA2→P3→P1;第二个子程序为逆圆子程序,刀具路径可规划为:P1→P3→TA2→P4→P2→TA1。具体的数控程序内容不再赘述。
根据前面所得的结论,在确定相应的刀具、切削用量、机床、夹具、工件材料及坯料后,可以对此凸轮零件进行数控加工仿真分析,仿真所得的刀具轨迹及凸轮第一面的加工结果如图3所示。

图3 零件数控加工仿真图
5 结论
主要研究了一种双面推力槽形凸轮的数控加工工艺及数值处理过程。在工艺处理中,针对具体的加工中心确定了工件的安装方式和定位基准、加工坐标系以及切削刀具和相关工艺参数等内容,并根据零件的结构特点和加工要求确定了合理的走刀路线,从而为零件的数控加工奠定了工艺基础。在数值处理中,以第一面的加工过程为例,说明了计算凸轮凹槽编程轨迹基点坐标的过程,并通过采用专门编制的运算程序完成了所有基点坐标的计算,从而为加工程序的正确编制提供了数据来源。本论文的研究结果为相似凸轮类零件的数控加工提供了理论依据,并在制定各种凸轮类零件数控加工工艺方面具有一定的实际参考价值。
[1]王永章.机床的数字控制技术[M].哈尔滨:哈尔滨工业大学出版社,1995.
[2]王仁德,赵春雨,张耀满.机床数控技术[M].沈阳:东北大学出版社,2002.
[3]范炳炎.数控加工程序编制[M].北京:航空工业出版社,1995.
[4]王亚辉.平面槽形凸轮零件的数控加工[J].工具技术,2009,43(7):77 -79.
[5]王林鸿,刘品潇.盘状沟槽凸轮的数控加工[J].机械工程师,2005(3):48-50.
[6]陈赛克,刘江涛.基于SolidWorks与Mastercam盘形槽凸轮的设计与数控加工[J].煤矿机械,2006,27(12):85-87.
[7]郭威,王水生,李华.基于实数编码遗传算法的轨迹综合优化设计[J].沈阳航空工业学院学报,2010,27(3):68-70.
[8]戴龙.对宽槽圆柱凸轮数控加工的探讨[J].宁夏机械,2005(1):36-37.
[9]林士龙,王阿春,纪俐,等.圆度误差评定方法及圆度误差统计分布的研究[J].沈阳航空工业学院学报,2009,26(4):27 -30.
[10]戴红,陈喆,姚娜.学用Visual Basic6.0[M].北京:清华大学出版社,1999.

