MATLAB优化工具箱在蜗杆传动优化设计中的应用

苗君明

(辽宁装备制造职业技术学院，辽宁 沈阳 110161)

蜗杆传动是在空间交错的两轴间传递运动和动力的一种传动机构。由于蜗轮蜗杆传动具有传动比大、传动平稳、结构紧凑等优点，所以在工程中的应用十分广泛。在蜗杆传动中，通常采用淬硬磨削的钢制蜗杆，而采用贵重金属的青铜等材料制造蜗轮齿轮，以使传动副具有良好的减摩性、耐磨性和抗胶合能力。为了节约贵重金属，降低成本，直径较大的蜗轮常采用组合结构。本文以MATLAB软件为平台，利用MATLAB优化工具箱进行优化设计，得到满足使用要求体积最小的蜗轮，从而节约贵重有色金属，节约了成本。

1 数学模型的建立

1.1 目标函数和设计变量

如图1所示，蜗轮齿圈的结构尺寸包括:齿顶圆直径 da、齿根圆直径 df、齿圈的外径 de、内径d0、齿宽b。蜗轮齿圈的体积为:

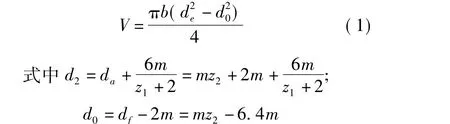
蜗轮齿数z2=uz1

式中，u是齿数比;z1是蜗杆齿数。

蜗轮齿宽b=ψda1=ψm(q+2)

式中q是直径系数

ψ是齿宽系数，当z1=1～2时，ψ=0.75;当z1=3～4时，ψ=0.67。

将上述关系代入蜗轮齿圈的体积计算式中，经过整理得到目标函数

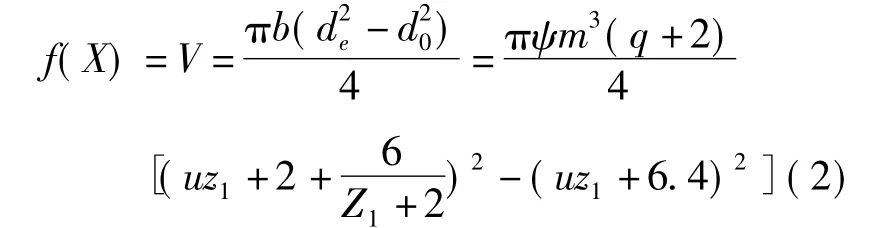
从上式可见，蜗轮齿圈的体积与蜗杆齿数z1、模数m、直径系数q和齿数比u的函数。由于齿数比u一般是已知量，因此，取蜗杆齿数z1、模数m、直径系数q作为设计变量，即

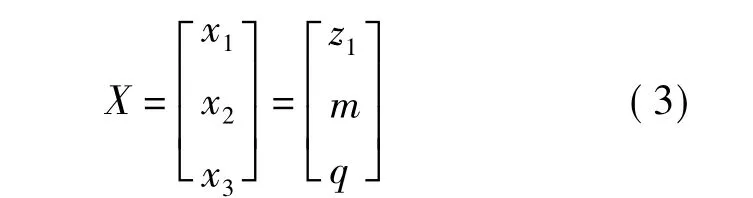
因此，目标函数可以写成

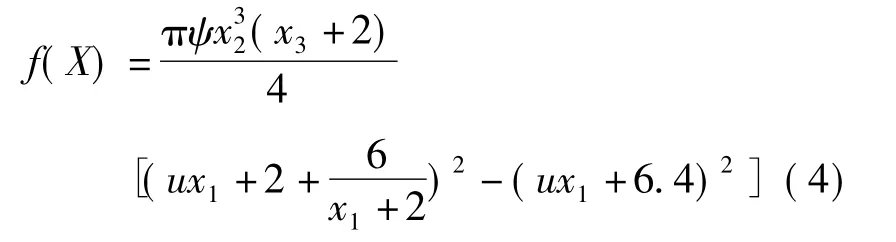
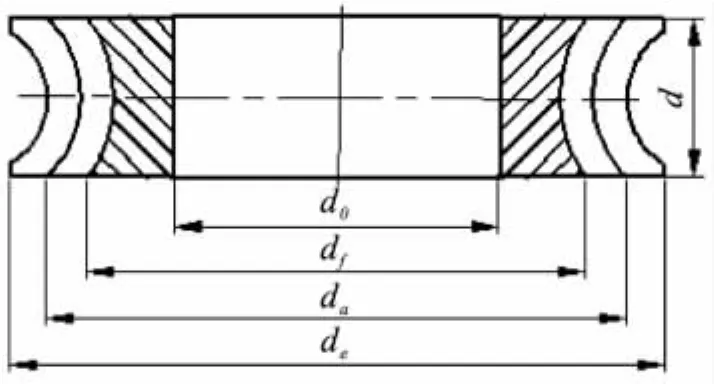
图1 蜗轮尺寸参数

1.2 约束条件

(1)蜗杆齿数的限制

对于动力传动，要求z1=2～4。因此有

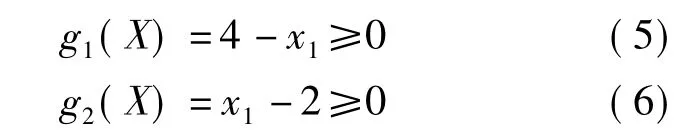
(2)蜗轮齿数的限制

一般要求z2=uz1=30～80。因此有

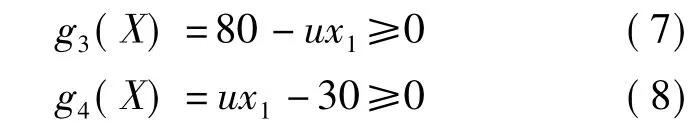
(3)模数的限制

对于中小功率的蜗杆动力传动，要求2≤m≤18。因此有

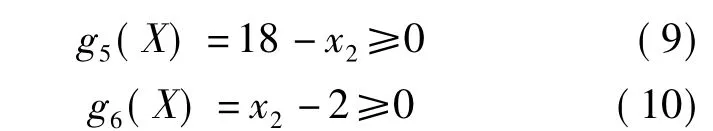
(4)蜗杆直径系数的限制

对应上述模数的范围，要求8≤q≤16。因此有

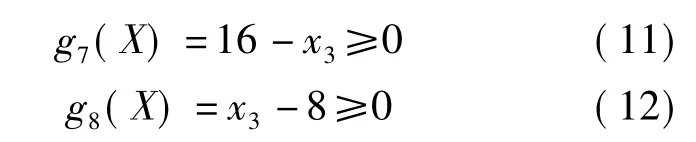
(5)蜗轮齿面接触强度的限制根据蜗轮齿面接触强度条件

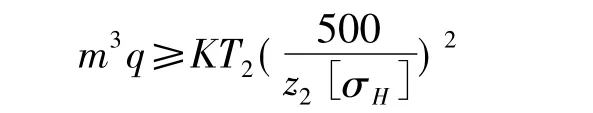
式中K是载荷系数;

T2是蜗轮传递的转矩;

［σH］是蜗轮齿圈材料的许用接触应力。

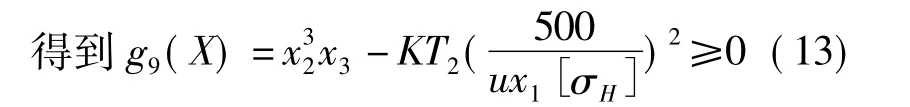
(6)蜗轮齿根弯曲强度的限制

由于蜗轮轮齿的齿根是圆弧形，抗弯能力较高，很少发生蜗轮轮齿折断。所以，对于闭式蜗杆传动，通常不再进行蜗轮齿根弯曲强度计算。

(7)蜗杆刚度的限制

要求蜗杆工作时最大挠度不大于m/50，即

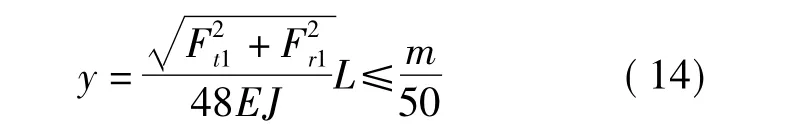
式中，蜗杆支承跨度L=0.9d2=0.9muz1

弹性模量E=2.1×105MPa

将上述关系代入上式整理得到

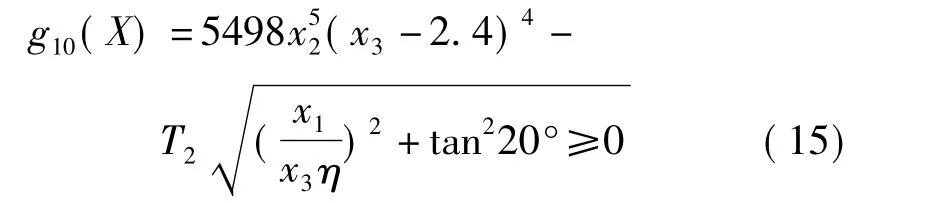
上述优化设计数学模型的约束条件共有8个边界约束和2个性能约束。

2 工程应用实例

已知某普通圆柱蜗杆传动的输出轴扭矩T2=9484 N·m，工作平稳(载荷系数K=1.21)，齿数比u=20，蜗轮齿圈材料为ZQSn10－1，许用接触应力［σ［H］］=268 MPa，传动效率 η =0.80。试按照蜗轮齿圈体积最小的要求进行优化设计。

2.1 传统设计方法

由选择蜗杆传动类型、按齿面接触疲劳强度进行设计、蜗杆与蜗轮的主要参数与几何尺寸、校核齿根弯曲疲劳强度等步骤确定蜗轮蜗杆传递的模数m、齿数z和直径系数q分别为8、2、10。蜗轮体积为1.6×105mm3。

2.2 利用MATLAB工具箱优化设计

(1)建立优化设计的数学模型

将已知数据代入目标公式，整理得到

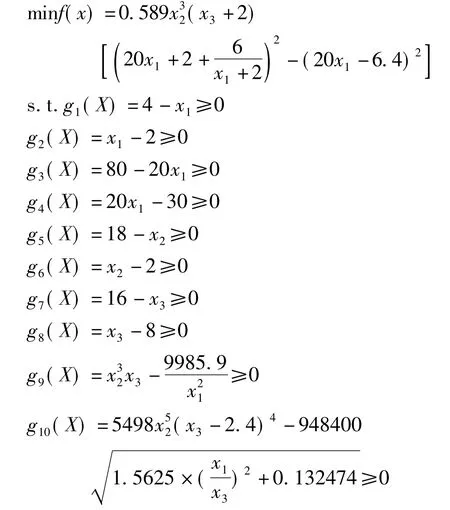
经过分析，约束条件 g1(X)≥0相对于g3(X)≥0来说是消极约束，约束条件g4(X)≥0相对于g2(X)≥0来说也是消极约束。因此，可以将g1(X)≥0和g4(X)≥0这两个消极约束条件去掉。可见，这是一个三维有8个不等式约束的非线性优化设计问题。

(2)优化方法与结果分析

采用MATlAB编写优化目标函数程序和约束函数程序，调用MATLAB的optimtool优化工具箱，初始值x=［123］，输入目标函数与限制函数名称。运行结果，X=［2.97228.564］，f=5.5795×104mm3。对于优化结果进行圆整，取离散最优化解:蜗杆齿数z1=3，模数m=2，直径系数q=9，则蜗轮齿圈体积V*=5.8118×104mm3。经检验，满足g(1)－g(10)的约束条件，符合设计要求，故优化结果可用。

3 结论

与传统设计方法比较，利用MATLAB优化工具箱对蜗轮蜗杆传动进行优化设计，大大地减小整个传动机构的体积，提高了经济效益和工作效率。

［1］杜东，马振，孙晓明.MATLAB遗传算法工具箱(GAOT)在水资源优化计算中的应用［J］.水利科技与经济，2007，13(2):73 －76.

［2］郭仁生.基于MATLAB和Pro/ENGINEER优化设计实例解析［M］.北京:机械工业出版社，2007.

［3］叶又东，肖华，王波.普通圆柱蜗杆传动的模糊优化设计［J］.机械制造与自动化，2004，33(4):19－22.

［4］邓晓红.蜗杆传动的优化设计［J］.淮海工学院学报，2005，14(4):21 －23.

［5］刘亚磊，郭登明，易先忠.基于MATLAB优化工具箱的机械优化设计［J］.现代机械.2006(6):32－33.

［6］童新华，李爱玲.基于MATLAB的外啮合齿轮泵结构优化［J］.机械，2010(37):29－31.

［7］张慧鹏.基于MATLAB的二级圆柱齿轮减速器优化设计［J］.机械设计与制造，2010(4):79－80.

［8］覃岭，谢君生，梁东城.基于MATLAB的链传动的可靠性优化设计［J］.机械传动，2009(3):67－69.