几种模型在平面坐标转换中的应用

姚朝龙，刘立龙

（桂林理工大学土木与建筑工程学院， 广西 桂林 541004）

几种模型在平面坐标转换中的应用

姚朝龙，刘立龙

（桂林理工大学土木与建筑工程学院， 广西 桂林 541004）

针对在平面坐标转换时选取不同模型将得到不同的转换精度，通过所编程序进行实验,对比了四参数模型、六参数模型和二次曲面模型的转换精度。实验表明，当合理选择转换点时二次曲面模型在平面坐标转换中精度高于四参数模型和六参数模型的转换精度。

平面坐标；坐标转换；转换模型；转换精度

随着测绘技术的发展，从常规的地面测量发展到卫星大地测量，在不同时期、不同地方获得了许多基于不同坐标系统的测量成果。由于地图坐标是从参考椭球经过投影转换为平面坐标，2个不同参考系统之间没有直接的数学关系[1]。此时，常常采用二维转换模型进行坐标转换。对于二维转换模型，参数的选取依赖于工程项目的需要，在大多数平面坐标转换应用中，常常使用四参数模型、六参数模型和二次曲面模型进行二维平面坐标转换。本文将对比四参数模型、六参数模型和二次曲面模型在平面坐标转换中的转换精度，得出算例的最佳模型。

1 模型及其参数求解

1.1 四参数模型

四参数模型[2]是从布尔莎公式演化而来的，其计算公式为:

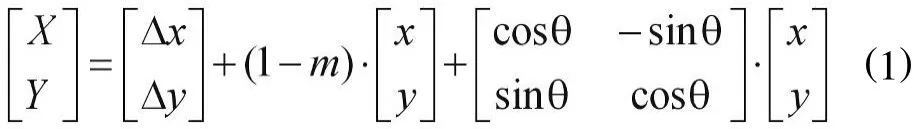
设所有转换点带有误差的观测值等权，则由式(3)的误差方程，通过间接平差法求得转换参数向量＾的最小二乘解为：（其中 P为单位权），从而求出。则平移参数为再

1.2 六参数模型

六参数模型[1,3]是一种平面仿射变换，将两坐标轴的指向经过2个角度旋转 和 ，并采用2个尺度因子，即纵向尺度因子x和横向尺度因子y。在任意2个平面坐标间的六参数仿射变换，可以用如下公式：

由以上两式可见，X和x、y之间存在线性关系，Y和x、y之间也存在线性关系，因此以上两式完全可以由线性回归原理进行解算。

用一个通用型线性回归模型代替以上两个式子，即

对于通用线性回归模型 (5)将 Z变为 X，则 k1、k2、k3即分别为a0、a1、a2；将Z变为Y，则分别为b0、b1、b2。

1.3 二次曲面模型

二次曲面模型[3,4]又称二次多项式拟合，是多项式变换中的一种，已知点在两坐标系间的坐标差异值可以用一个多项式来拟合，然后用这个多项式来预计其他点的坐标差异值。在坐标系转换中，通常采用二次曲面模型进行拟合。其计算公式如下：

式 中，a0、a1、a2、a3、a4、a5、b0、b1、b2、b3、b4、b5为转换参数，当转换点个数多于 6个时，可以通过最小二乘法结合线性回归原理求解转换参数，其求解过程与六参数模型参数解算相似。

2 算例分析

所用算例数据[5]共15个公共点，其中10个点作为转换点，用于求解转换参数，5个点作为检验点，点位分布如图 1所示。为了对比四参数模型、六参数模型和二次曲面模型在两平面坐标系的转换精度，本文采用笔者利用VB所编坐标转换程序进行坐标转换，并进行精度分析。

图1 公共点点位分布图

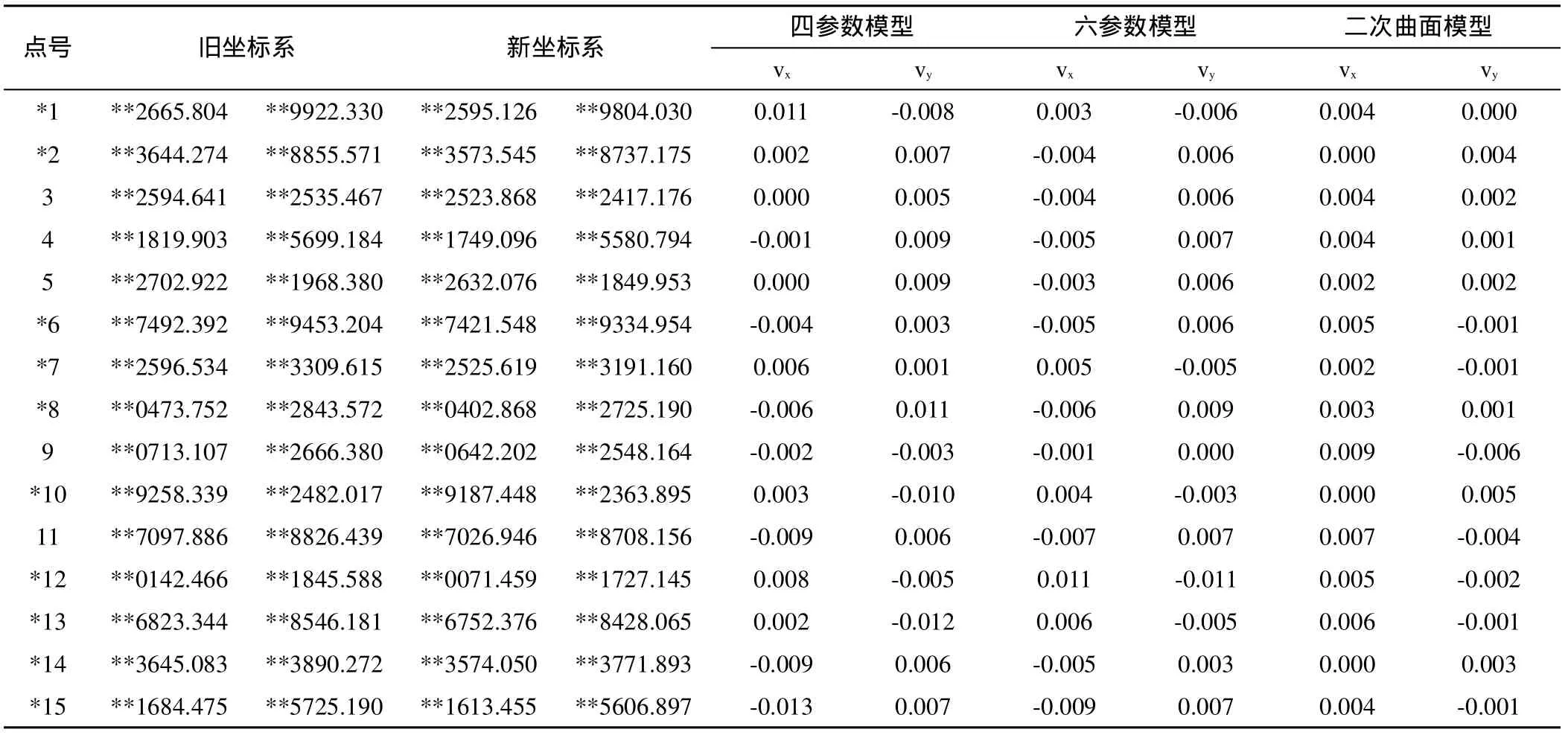
表1 三种模型的转换残差比较/m

表2 转换残差统计表/m

其中x'、y'为转换后坐标值，x、y为同名点原坐标值。

坐标分量X、Y转换中误差：

当计算内符合精度，n为转换点个数；计算外符合精度，n为检验点个数。

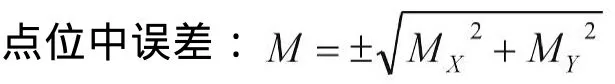
从表1、表2可以看出，四参数模型和六参数模型的最大、最小转换残差绝对值都在1 cm左右，六参数模型的内符合精度优于四参数模型，外符合精度与四参数模型相同。二次曲面模型的转换精度均高于四参数模型和六参数模型的转换精度，其最大、最小转换残差绝对值都在mm级，转换点内、外符合点位中误差也达到了mm级。

3 结 语

本文通过对比 3种模型在平面坐标转换中的转换精度可以看出，当选择合理的转换点点位和转换点个数进行转换参数的求解时，3种模型的转换精度都在cm级范围内，由于六参数模型采用了2个旋转参数和2个尺度因子，其转换精度比四参数模型的转换精度高，而二次曲面模型由于考虑了系统畸变的影响，在2种转换模型中转换精度最高，达到mm级。

[1] GUORonggang.System ticalAnalysisof the Transformation Procedures in Baden-Württemberg w ith Least Sqrares and Total LeastSquaresMethods[D].Stuttgart,Universit?tStuttgart,2007

[2] 刘科利.北京54和西安80坐标系下的坐标转换及精度分析在Excel中的实现[J].勘察科学技术，2008(5):24-27

[3] 姜晨光.用线性回归方法将GPS坐标转为地方坐标[J].测绘科技通讯，1998(1)：17-19

[4] 徐生望,周建国,王超.坐标转换模型问题研究[J].西部探矿工程，2009(2)：162-165

[5] 褚永海,田福娟,马晶.局部坐标转换方法与应用[J].湖北水利水电职业技术学院学报，2006，2(1)：42-47

[6] 秦永乐.Visual Basic测绘程序设计[M].郑州：黄河水利出版社，2005

[7] 王诚,王昶.曲面模型在北京54坐标系到西安80坐标转换精度的探讨[J].矿山测量，2009,12(6):84-86

[8] 丁士俊，张忠明.几种不同坐标变换方法问题的研究[J].四川测绘，2005,28(1):16-19

Application of SeveralModels to Plane Coordinate Transformation

by YAO Chaolong

Aiming at the coordinate transformation between two 2D coordinate systems,diffrient accuracies from diffrientmodelsw ill be achieved.This paper utilized the program to compare the accuracy of four-parametermodel,six-parametermodel and second-degree polynom ialmodel.Results from testing showed when reasonable choose transforming points,theaccuracy of second-degree polynomialmodelisbetter than theaccuraciesof four-parametermodeland six-parametermodelin2D coordinate transformation.

plane coordinate systems,coordinate transformation,conversion model, transformation accuracy （Page:64）

P226.3

B

1672-4623(2011)02-0064-03

2010-01-14

项目来源：国家自然科学基金资助项目（41064001）。

姚朝龙，硕士，主要从事测绘信息采集与数据处理研究。