单相逆变器迭代学习控制应用研究

叶建华，曹 旭

(上海电力学院电力与自动化工程学院，上海200090)

在日益兴起的分布式发电系统研究中，逆变器作为广泛采用的能量转换及接口器件，其性能对于分布式发电系统的稳定、高效运行起着十分重要的作用.逆变器输出波形的质量是衡量逆变器性能的重要指标［1］.单纯采用 PID控制的PWM逆变器存在跟踪正弦波形不精确，易受非线性负载影响造成电压、电流畸变等不利因素.

迭代学习控制(Iterative Learning Control，ILC)着眼于利用受控对象和目标轨道的周期性或重复性，起初应用在重复性机械运动结构的控制中，由于其不需要依赖控制对象的精确数学模型、结构简单，以及具有良好的跟踪精度等特点获得了广泛的关注.本文将迭代学习控制应用于逆变器输出波形的控制，以期解决逆变器跟踪正弦波形不精确等问题.

1 迭代学习控制

迭代学习控制的基本思想是:在被控系统作重复运动且结构特性不变的前提下，利用控制器先前的控制经验逐渐寻找理想的输入特性曲线，使被控对象精确地按期望轨迹运动［2，3］.于是可将一重复运动轨迹(如正弦波)按周期分为若干次控制过程，如图1所示.

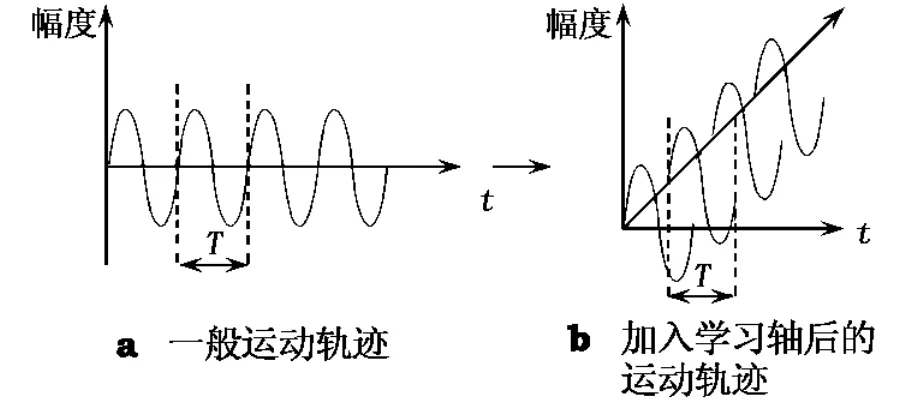
图1 学习控制基本思想

迭代学习跟踪控制的目标是要获得一个控制序列ud(n)，使得系统输出y(n)精确跟踪理想输出yd(n).迭代学习的基本原理是利用上一次工作周期内的误差ek(n)，对下一次工作周期的控制输入uk+1(n)进行修正，经过多个工作周期的学习，逐渐使实际输出y(n)收敛于理想输出yd(n).

迭代学习的控制算法有:PID型学习算法，高阶迭代学习算法，具有遗忘因子的学习算法，基于2-D系统理论的学习算法等［3］.PID型学习算法分为开环学习和闭环学习.开环PID学习算法是第k+1次的控制等于第k次的控制加上第k次输出误差的PID校正项，即:

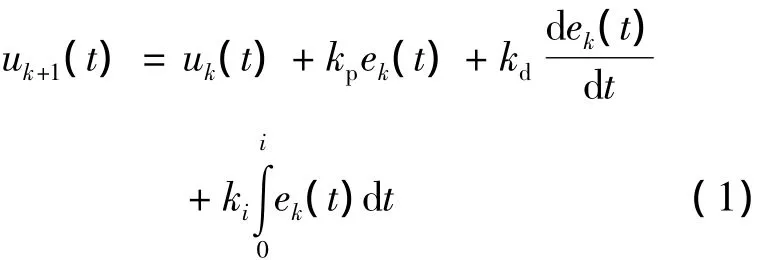
式中:kp——比例;

kd——微分;

ki——积分学习增益.

闭环PID学习算法是取第k+1次运行的误差作为学习的修正项，即:

按照学习方式的不同，PID型学习算法可分为开环学习和闭环学习［2，4］:前者是指每次控制指令的大小只和前一次控制指令及前一次轨迹误差相关，与当前的轨迹误差无关;后者是指每次控制指令的大小只与前一次控制指令及当前的误差轨迹相关.这两种学习方式的控制框图见图2和图3.在传统学习控制中学习方式可选择P型、PI型和 PID 型等［2，3］.

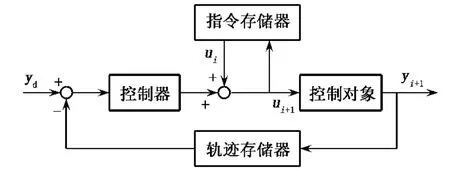
图2 开环学习控制

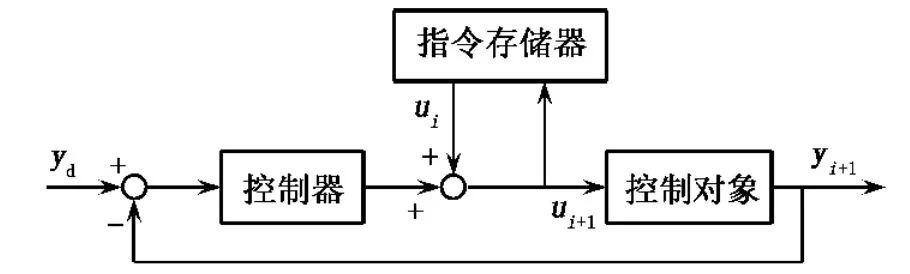
图3 闭环学习控制

2 P型学习率的收敛性判定

收敛性是迭代学习控制理论的中心问题.学习算法的稳定性是保证学习控制能够运行的基本前提，其作用是随着学习次数的增加，保证控制系统不发散.但对于学习控制系统而言，仅仅稳定是不够的，只有使学习过程收敛到真值，才能保证得到的控制为某种意义下的最优控制.目前，从最初的时不变系统到线性时变系统再到非线性系统，从连续系统到离散系统都有大量的具有稳定性和收敛性的学习律［3］.

对于P型学习控制的开环学习收敛定理，考虑如下的连续系统:

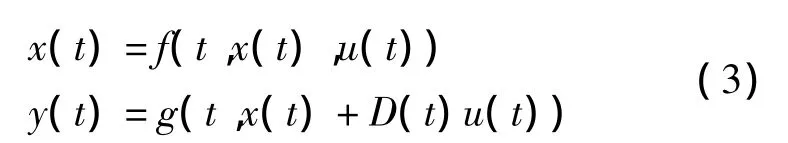
若采用如下开环P型学习律

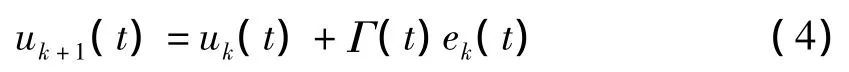
系统式(3)在t∈［0，T］中需满足下列条件:

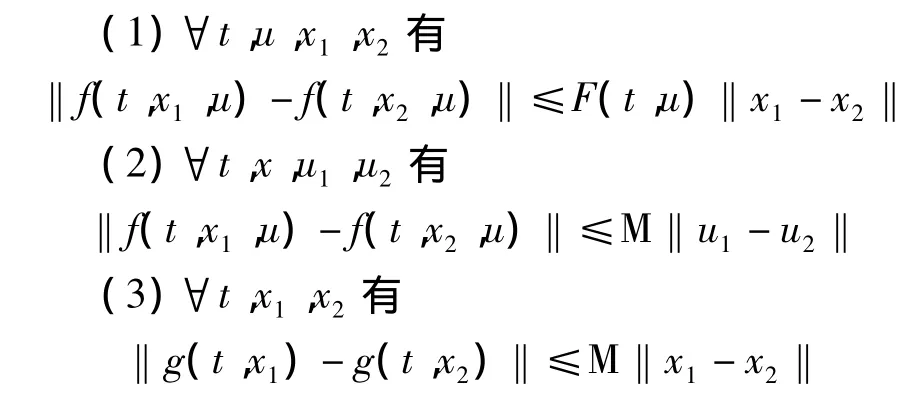
(4)每次运行时的初始误差{δxk(0)}k≥0为一收敛到零的序列;

(5)存在唯一的理想控制ud(t)使得系统的状态和输出为期望值xd(t)，yd(t)，其中 F(t，u)为t，u的连续函数，M为一正的常数.

此时，对于任意给定的初始控制u0(t)及每次运行的初始状态xk(0)所得序列皆对t一致地收敛到xd(t)，yd(t)，ud(t)的充分条件为谱半径:

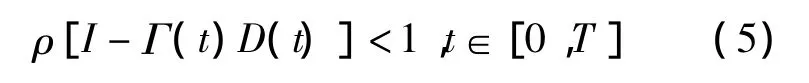
其必要条件为:

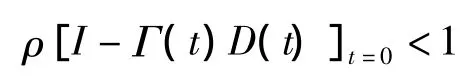
若Γ(t)，D(t)为常数矩阵，则式(5)成为充分必要条件.

若采用闭环学习收敛定理，考虑系统为式(3)，则有:

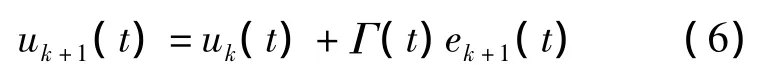
系统式(3)在t∈［0，T］中满足下列条件:

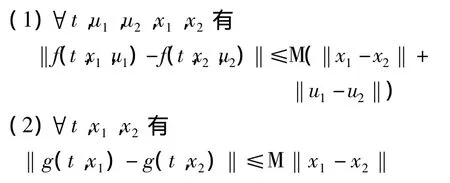
(3)每次运行时的初始误差{δxk(0)}k≥0为一收敛到零的序列.

(4)存在唯一的理想控制ud(t)使得系统的状态和输出为期望值xd(t)，yd(t).

(5)(I+Γ(t)D(t)－1)存在，(1)至(2)中的M为一正的常数，则对于任意给定的初始控制u0(t)及每次运行的初始状态xk(0)，所得的序列皆对t一致地收敛到xd(t)，yd(t)，ud(t)的充分条件为谱半径

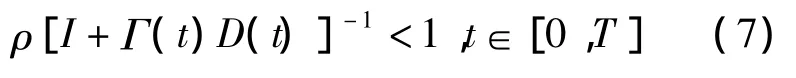
其必要条件为

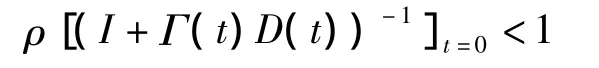
若Γ(t)，D(t)为常数矩阵，则式(5)成为充分必要条件.

3 仿真比较

3.1 系统结构

逆变器的控制结构为传统的双环PWM控制，由于非线性负载的存在，会使得逆变器的输出电压波形产生畸变.本文在电压外环上采用ILC控制器取代传统的PID控制器.ILC控制器又分别采用比例型开环学习和比例型闭环学习两种形式，并将其效果与PID控制器效果进行比较.所采用的主系统参数为:直流母线电压400 V，输出交流电压的有效值为220 V，频率为50 Hz，负载为二极管整流型负载，其系统结构见图4.

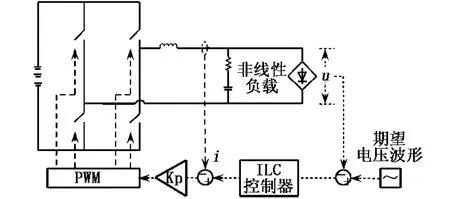
图4 系统结构示意

3.2 仿真波形

当电压外环采用PID控制器时，逆变器输出波形U出现了明显的畸变，电压有效值跌落至199 V，总谐波含量THD达到了7.6%.

当采用开环学习型ILC控制器后，逆变器的输出波形有了一定的改善，电压有效值恢复至218 V，总谐波含量THD降至4.8%.但是开环学习型ILC的输出只与上一周期的输出及误差有关，因此控制器作用会有一个周波的延迟，如图5所示.

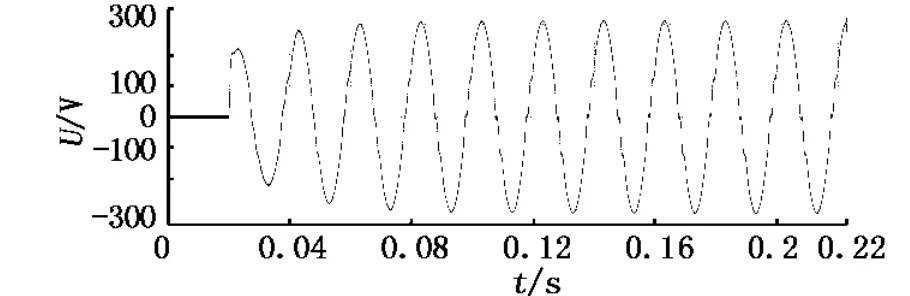
图5 采用开环学习ILC控制器时输出电压U波形

当采用闭环学习型ILC控制器后，逆变器的输出波形获得了较大的改善，电压有效值恢复至220 V，总谐波含量THD降至0.9%.由于闭环学习控制的输出不仅与当前误差相关，也与上一周期的控制输出相关，真正起到了“学习过去经验并根据当前误差进行调节”的作用，从而获得了较好的控制效果.

虽然ILC控制器有着较好的稳态性能，能够精确地跟踪期望波形，但是在其学习过程中，系统的动态性能表现得并不理想，这一点在开环学习中显得尤为明显(见图5).即便是仿真效果较好的闭环学习方式也需要经过3-4个周波才能完成学习过程，在该过程中电压有效值最低至211 V，THD含量最高达5.8%，具体见图6.因此，在今后需要进一步研究如何改善迭代学习控制动态性能的方法.

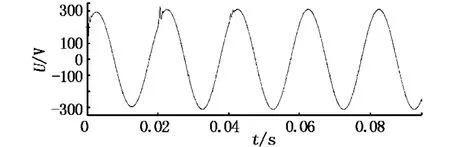
图6 闭环学习ILC控制器的学习过程

在仿真过程中发现，采用PI型学习律的ILC控制器相对P型学习律的ILC控制器在控制效果上并无明显提高，而PI型学习律相对P型学习律在学习轴上并无变化，只是在时间轴上加入了积分器.同时，积分器在频域上仅能对低频信号实现良好的无差调节效果，而高频的交流轨迹和跟踪误差则很难调节.P型学习律的误差曲线见图7.

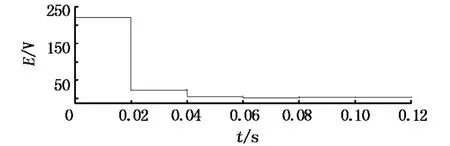
图7 P型学习律的误差曲线

另外，鉴于在数字控制器中微分器D采用较小的微分步长做除数会放大测量信号的误差，从而造成系统失稳，因此较少采用PD型学习律.

4 结语

本文针对传统PWM双环控制逆变器在非线性负载工况下出现的输出电压波形畸变问题，应用迭代学习控制方法对其进行改善，仿真结果表明该方法是可行的，在学习过程结束后，逆变器的输出波形得到了较大改善.同时，在周期性过程的迭代学习控制应用中，需要注意其不够理想的动态性能.在今后的研究中可以将迭代学习控制与其他具有良好动态性能的控制方法相结合，以获得既有良好动态性能又具有高精度跟踪性能的控制器.

［1］庞庆，王震，占江山.基于重复学习控制的400 Hz逆变电源研究［J］.电力电子技术，2010，44(5):67-69.

［2］于少娟，齐向东，吴聚华.迭代学习控制理论及应用［M］.北京:机械工业出版社，2005:6-9.

［3］谢胜利，田森平，谢振东.迭代学习控制的理论与应用［M］.北京:科学出版社，2005:3-12.

［4］许建新，侯忠生.学习控制的现状与展望［J］.自动化学报，2005，31(6):943-953.