三端点区间数互反判断矩阵的一致性测度方法

张 娜

0 引言

多属性决策指在考虑多个指标或属性的情况下，为选择最佳方案或进行方案排序而进行的决策问题[1]。目前，大量的多指标决策问题已经被广泛的应用于社会、经济、管理、环境等各个领域。随着社会、经济的发展，决策问题的复杂性、不确定性以及人类思维的模糊性不断增强，在实际决策过程中，专家的偏好信息经常以不确定性的形式表示，如区间数、模糊数等，相关研究[2～10]得到了学术界的重视。但现有的区间数和模糊数方法，存在以下不足之处：区间数在某些决策情况下有时为了覆盖整个取值范围，区间可能取得过大；三角模糊数通常假设端点两两之间呈线性关系，极大地限制了决策者偏好的表达。以教师绩效考核评价为例，专家对教师绩效的打分的取值范围为[60,90]，分值差异很大，这时如果认为整个区间的取值机会相等，就会使得出的结果有很大的偏差，很难判断其真实绩效。若利用三角模糊数(60,70,90)来表示，由于现有处理方法一般需要事先假定可能性成线性方式分布，而实际上分布方式更难以确定。文献[11]探讨了区间数和三角模糊数在刻划不确定信息时的局限性以及优势互补性，提出了三端点区间数的概念。对于决策信息为三端点区间数的情况，也有研究成果出现[12～14]。三端点区间数既将保持了区间的取值范围，又突出了取值可能性最大的重心点，在一定程度上弥补了两端点区间数取值范围过大、重心不明确的缺陷。

目前有关三端点区间数互反判断矩阵及其一致性测度方法的研究较少，文献[11]给出了三端点区间数互反判断矩阵完全一致性定义，但此定义给出的条件不是太强，本文将认为其完全一致性的定义应该为一致性定义。基于此，本文将定义三端点区间数互反判断矩阵的完全一致性、一致性和满意一致性的概念并讨论它们之间的关系；给出完全一致性、一致性和满意一致性的测度方法。最后给出具体的算例，验证所提出方法的有效性和适用性。

图1 三端点区间数示意图

1 三端点区间数及其互反判断矩阵的定义

本文涉及的区间数、区间数互反判断矩阵的相关概念以及三端点区间数的运算见文献[1]、[2]、[4]、[11]等。

在群决策中，采用三端点区间数方法来表达偏好，同时考虑了区间范围以及最可能判断点，充分利用了已知决策信息，并有效避免了信息丢失，在一些决策情况下更符合实际。

定义1[11]设R为实数域，称闭区间[cijL,cijM,cijU]为三端点区间数，其中cijL代表下限值，cijU代表上限值，cijM代表最可能值，且cijL≤cijM≤cijU，见图1。

在群决策背景下，可以利用以下方法得到三端点区间数：对于单决策者的决策情况，决策先估计区间的上、下限值[cijL,cijU]，同时可以得到其它可能值的概率P(cij)，对于cijM应选择可能值的最大概率，并且应该满足Max[P(cij)]≥δ（δ为一常数，δ越大表明决策者偏好越集中，δ=1时该决策退化为普通数字即cijL=cijM=cijU）；对于多决策者的决策情况，可以采用数理统计方法拟合决策者的意见即可得到表达决策群体偏好的三端点区间数，即若决策者数位m，对于任意的cij统计cijk出现的频数vk,k=1,2,…,L，其中L为决策者的分类数（vk≤m），则P(cijk)，群体决策偏好可以表示为三端点区间数[cijL,cijM,cijU]的形式[14]。

定义2 称Cˉ=(cˉij)n×n为n阶三端点区间数互反判断矩阵，cijL≤ cijM≤ cijU，cˉij=[cijL,cijM,cijU]，cˉji=[1/cijU,1/cijM,1/cijL]，且 cˉii=[1,1,1]。

2 三端点区间数互反判断矩阵的一致性相关定义

定义3[11]记wi(i=1,2,…,n)为三端点区间数互反判断矩阵导出的权重，若式（1）成立，则称三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n具有完全一致性；若不存在 wi满足式（1），则称其不具有完全一致性。

定义3虽然说明了决策者的一致性判断与最可能值相符合，但是其给出的定义条件不是太强，通过此条件只可以得到最可能值的权重wiM。而要想了解群体的总意图，必须得到权重的分布范围，即[wiL,wiM,wiU]，为此本文重新定义了三端点区间数互补判断矩阵完全一致性的概念。

定义4 称三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有完全一致性，若对于∀i＜k＜l均有cij=cikckj。

引理1[2]数字互反判断矩阵A具有一致性的充分必要条件是，存在向量v=(v1,v2,…,vn)T使得，其中成立。

定义5 称三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有一致性，若对于三端点区间数互反判断最可能值数字矩阵(cˉijM)n×n具有一致性，即 cˉijM=cˉikMcˉkjM；i,k,j=1,2,…,n 。

定义5说明：若专家给出的三端点区间数互反判断最可能值数字矩阵具有一致性，表明专家给出的偏好含有一致性信息，根据此偏好信息可以得到比较合理的排序；若不具有一致性，说明专家给出的偏好信息不合理，若有条件最好进行修正。

定理1定义3的完全一致性条件等价于定义5的一致性条件。

证明：设定义3的三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n具有完全一致性，则有，i,j=1,2,…,n；i≠j。 对 三 端 点 区 间数 最 可 能 值数 字 矩 阵 (cˉijM)n×n，，即三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n满足定义5一致性条件。

设三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n满足定义5的一致性条件，那么 (cˉijM)n×n具有一致性，即 cˉijM=cˉikMcˉkjM，根据引理1可得，存在向量 w=(w1,w2,…,wn)T，使得成立，令wi(i=1,2,…,n)为三端点区间数互反判断矩阵导出的权重，式（1）成立，故三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n满足定义3完全一致性的概念。证毕。

定理2 设 Cˉ=(cˉij)n×n为三端点区间数互反判断矩阵，若Cˉ具有完全一致性，则其具有一致性。

证明：设 Cˉ=(cˉij)n×n为三端点区间数互反判断矩阵，要证明Cˉ具有一致性，只需要证明最可能值数字矩阵(cˉijM)n×n具有一致性，即 cˉijM=cˉikMcˉkjM;i,k,j=1,2,…,n 。由定义 4及三端点区间数的运算可知，对于∀i＜k＜l，有cij=cikckj时，最可能值数字矩阵 cˉijM=cˉikMcˉkjM必然成立。证毕。

定理2研究了定义4与定义5的关系，得出若一个三端点区间数互反判断矩阵具有完全一致性，那么其一定具有一致性。

定理3 定义4中三端点区间数互反判断矩阵Cˉ=(cˉij)n×n完全一致性的定义可以得到三端点区间数权重的分布范围[wiL,wiM,wiU]。

证明：由定理1和定理2可知，若Cˉ具有完全一致性，则其具有一致性，即存在向量wM=(w1M,,…,)T使得，(i,j∈N)其中 wiM＞0(i∈N)，且=1成立，此条件只可以得到最可能值的权重wiM，权重范围[wiL,wiU]可根据两端点区间数互反判断矩阵一致性定义得到，具体见文献[15]。因此，若Cˉ具有完全一致性，可以得到三端点区间数权重[wiL,wiM,wiU]。证毕。

定理4 三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有一致性当且仅当凸集Sw非空，其中

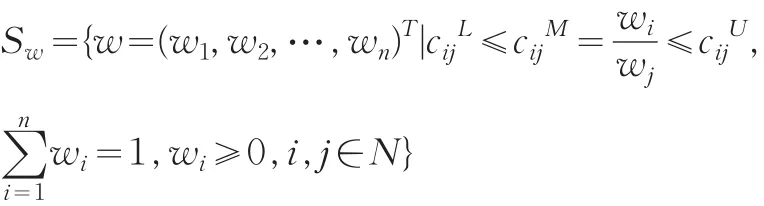
证明：设 Cˉ=(cˉij)n×n为三端点区间数互反判断矩阵，若 Cˉ具有一致性，根据定义5可知，有 cˉijM=cˉikMcˉkjM;i,k,j=1,2,…,n，则由引理1易知Sw非空。若凸集Sw非空，则不妨设w=(w1,w2,…,wn)T是Sw中一个元素，对于任意的i,j∈N，令而且cM=cMcM;i,k,j=1,2,…,n，由定义5ijikkj可知 Cˉ=(cˉij)n×n具有一致性。 证毕。

定理5 三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有一致性的充分必要条件是

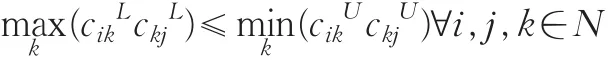
证明：若三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n具有一致性，则凸集Sw非空，即存在向量w=(w1,w2,…,wn)T使得下列不等式成立：

当三端点区间数互反判断矩阵不具有一致性时，可以由定义6判别它是否具有满意一致性。

定义6 称三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有满意一致性，如果存在实数互反判断矩阵 C͂M=(c͂ijM)n×n（c͂ijM∈[(1-δij)cijM,(1+δij)cijM]）具有一致性，其中 δij为允许决策的偏差。δij越大满意一致性越差，决策偏好越分散；δij越小满意一致性越强，决策偏好越集中。

定理6 三端点区间数互反判断矩阵Cˉ=(cˉij)n×n具有一致性，则必具有满意一致性。

证明：若三端点区间数互反判断矩阵 Cˉ=(cˉij)n×n具有一致性，则三端点区间数互反判断最可能值数字矩阵(cˉijM)n×n具有一致性，令 C͂M=(c͂ijM)n×n=(cˉijM)n×n，存在实数互反判断矩阵 C͂M=(c͂ijM)n×n（c͂ijM∈[(1- δij)cijM,(1+ δij)cijM]）具有一致性（其中 δij=0），根据定义6可知 Cˉ=(cˉij)n×n具有满意一致性。

定理6研究了定义5与定义6的关系，得出若一个三端点区间数互反判断矩阵具有一致性，那么其一定具有满意一致性。

定理7 存在实数互反判断矩阵 C͂M=(c͂ijM)n×n(c͂ijM∈[(1-δij)cijM,(1+δij)cijM])具有一致性的充分必要条件是对于任意i＜j∈N ，有

证明：若存在实数互反判断矩阵 C͂M=(c͂ijM)n×n(c͂ijM∈[(1-δij)cijM,(1+δij)cijM])具有一致性，根据文献[5]实数互反判断矩阵具有一致性的定义可知，对于任意的i,k,j∈N，都有

又由于

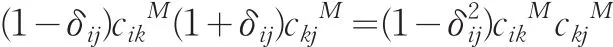
所以，对于任意的i＜j∈N，有

若对于任意的i＜j∈N ，有

令：

于是有

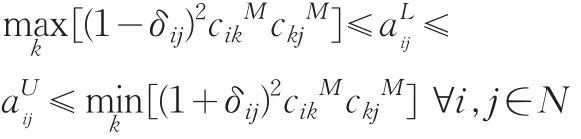
由定理5可知[(1-δij)cijM,(1+δij)cijM]构成的矩阵具有一致性。由定理4可知凸集Sw非空，所以存在实数互反判断矩阵 C͂M=(c͂ijM)n×n(c͂ijM∈[(1-δij)cijM,(1+δij)cijM]) 具有一致性。证毕。

3 算例分析

算例1设3个方案的决策问题有三端点区间数互反判断矩阵：

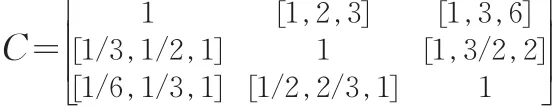
由于[1,2,3]×[1,3/2,2]=[1,3,6]，根据定义4可知C具有完全一致性。根据定义5证明C具有一致性。

算例2设4个方案的决策问题有三端点区间数互反判断矩阵：

由于c12c23=[1,2,3]×[1,2,4]=[1,4,12]，c13=[3,4,5]≠c12c23，所以三端点区间数互反判断矩阵C不具有完全一致性。

但C的最可能值数字矩阵为：

对于 ∀i（k,j=1,2,3,4），有 cijM=cikMckjM，因此三端点区间数互反判断矩阵C具有一致性。

上面分析可以看出三端点区间数互反判断矩阵C不具有完全一致性，但具有一致性。

算例3设3个方案的决策问题有三端点区间数互反判断矩阵：

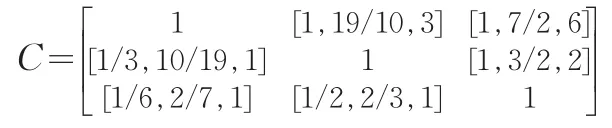
由于C的最可能值数字矩阵为：

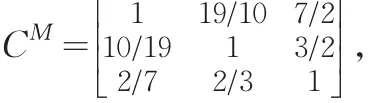
由于c13M=7/2，c12Mc23M=57/20，c13M≠c12Mc23M，因此三端点区间数互反判断矩阵C不具有一致性。

根据定义6及定理7判断其是否具有满意一致性，设δij=0.2为允许决策的偏差。

对于任意i＜j，有

由于对于任意i＜j∈N ，有

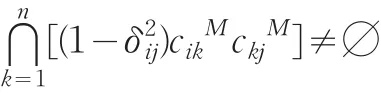
所以三端点区间数互反判断矩阵C在δij=0.2允许决策的偏差范围内具有满意一致性。

4 结论

目前国内外学者关于三端点区间数互反判断矩阵的一致性测度的研究尚处于起步阶段。为此，本文对其进行了深入研究，提出了三端点区间数互反判断矩阵的完全一致性、一致性、以及满意一致性定义，并讨论了它们之间的关系，具有一定的理论意义。若决策者给出的偏好信息满足完全一致性，说明决策者给出的所有信息都具有一致性，都是合理信息；若决策者给出的偏好信息满足一致性，说明此信息含有一致性信息，可以根据此信息求解出合理的最可能权重向量；若决策者给出的信息不满足一致性，如果可能的话最好对偏好信息进行改进，否则若满足满意一致性，说明此信息在一定可信度范围内含有一致性信息，对三端点区间数互反判断矩阵一致性定义的讨论为多属性决策方法的研究提供了更加合理的理论依据。对于满足不同一致性的三端点区间数互反判断矩阵，如何选用更合理的排序方法是今后进一步研究的方向。

[1]徐玖平,吴巍.多属性决策的理论与方法[M].北京:清华大学出版社,2006．

[2]Saaty T.The Analytic Hierarchy Process[M].NewYork:McGraw-Hill,1980.

[3]樊治平,尤天慧,张尧.属性权重信息不完全的区间数多属性决策方法[J].东北大学学报,自然科学版,2005,26(8)．

[4]魏贵武.对方案有偏好的区间直觉模糊多属性决策方法[J].系统工程与电子技术,2009,31(1)．

[5]钱钢，冯向前，徐泽水.区间数互补判断矩阵的一致性[J].控制与决策，2009，24（5）．

[6]Wang YM,Yang JB,Yang DL.Interval Weight Generation Approaches Based on Consistency Test and Interval Comparison Matrices[J].Applied Mathematics and Computation,2005,（167）.

[7]徐泽水，达庆利.三种基于互反判断矩阵的互补判断矩阵排序法[J].东南大学学报，2001，31（5）．

[8]Jahanshahloo GR,Hosseinzade L,Izadikhah M.An Algorithmic Method to Extend Topsis for Decision-making Problems with Interval Data[J].Applied Mathematicsand Computation,2006,175(2).

[9]Xu Z S.Projection Method for Uncertain Multi-attribute Decision Making With Preference Information on Alternatives[J].International Journal of Information Technology&Decision Making,2004,3(3).

[10]Xu Z S.On Similarity Measures of Interval-valued Intuitionist Fuzzy Sets and their Application to Pattern Recognitions[J].Journal of Southeast University,2007,23(1).

[11]朱建军,刘思峰,王华.群决策中两类三端点区间数判断矩阵的集结方法[J].自动化学报,2007,33（3）．

[12]朱建军,陈立光,刘思峰.用于原纸规格精简决策的三端点区间数层次分析法[J].系统工程理论与实践,2007,27(10)．

[13]朱建军,宋传平,刘思峰.一种三端点区间数判断矩阵的一致性及权重研究[J].系统工程学报,2008,23（1）．

[14]田飞,朱建军,姚冬蓓,朱红燕.三端点区间数互补判断矩阵的一致性及权重[J].系统工程理论与实践,2008,（10）．

[15]杜俊慧，魏法杰.区间数互反判断矩阵一致性及排序[J].系统工程，2008,26（9）．