一类双险种复合Poisson-Geometric过程风险模型
彭朝晖,甘 柳,晏小兵
0 引言
在风险理论中,古典风险模型经过较长时间的完善和补充,已经成为最完美的风险理论。而古典风险模型中,索赔来到过程是一个Poisson过程,Poisson过程的一个重要性质是均值等于方差,但在保险公司的实际运作中是难以具备这样的性质的。为了使模型更加符合实际,不少人对索赔来到过程进行了推广,其中文献[1]提出了一类称为复合Poisson-Geometric过程的计数过程,建立了如下模型:

其中,U(t)为保险公司在t时刻的盈余量,c为单位时间内收取的保费,u≥0为公司的初始盈余,{N(t);t≥0}是参数为λ、ρ的复合Poisson-Geometric过程,Xi表示第i次索赔额。针对模型(1),文献[1]给出了其破产概率所满足的更新方程,并在索赔额Xi服从指数分布时,得到了破产概率的显示表达式;文献[2]在索赔分布Xi为相位分布的情况下,得到了破产概率的显示表达式,并进行了数值计算;文献[3]得到了Gerber-Shiu折现罚金函数。
随着保险公司经营规模的不断扩大,险种日益呈现多元化,近年来也有不少研究了多险种的风险模型,例如:文献[4]对两个险种的索赔到达过程均为齐次Poisson过程的风险模型进行了研究,得到了破产概率的近似表达;文献[5]和[6]在此基础上对将各个险种的保费收入过程{ct;t≥0}推广为Poisson过程或复合Poisson过程;在此基础上文献[7]将保费收入过程推广为两个独立复合Poisson过程之和;文献[8]则将文献[5]~[7]纳入一个框架之下,即它们都可以表示成为两个独立的谱正Lévy过程的差,并研究了这一类模型的首达时的性质和生存概率的Pollaczek-Khinchin公式。
本文拟建立一类双险种风险模型,一个险种的索赔来到过为复合Poisson-Geometric过程,另一个险种的索赔来到过程的时间间隔服从广义的Erlang(n)分布。然后得到Gerber-Shiu折现罚金函数所满足的积分微分方程,利用鞅方法得到了该模型的Lundberg方程,并且利用Laplace变换给出初始资本为0时的Gerber-Shiu折现罚金函的精确解。
1 模型定义
我们考虑如下模型:
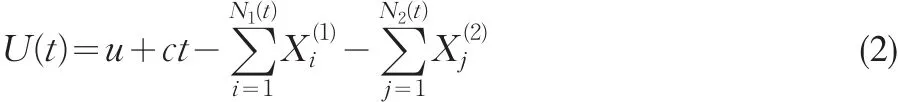
其中,{X(1)i,i=1,2,…}和{X(2)j,j=1,2,…}分别为两相互独立的随机变量序列,其分布函数分别为F(x)和G(x),密度函数分别为 f(x)和g(x),均值为 μ1和 μ2。{N1(t);t≥0}是参数为λ,ρ的复合Poisson-Geometric过程,{N2(t);t≥0}独立于{N1(t);t≥0},是一个更新过程,其来到的时间间隔{Vi}i≥1,这里假设{}Vii≥1服 从 广 义 的 Erlang(n)分 布,参 数 为λ1,λ2,…,λn,即Vi可以分解为Vi=Vi1+Vi2+…+Vin。其中Vij服从均值为1λj的指数分布。
为了保证保险公司经营稳定,单位时间内的保费收入应大于其单位时间内的理赔,即:

本文恒设式(3)成立。
定义1 设 λ>0,0≤ρ<1,称 {N(t);t≥0}是参数为 λ,ρ的复合Poisson-Geometric过程,如果
(1)N(0)=0;
(2){N(t);t≥0}具有平稳独立增量;
(3)对 t≥0有 N(t)~PG(λt,ρ)
设保险公司初始准备金为u,破产时刻为Tu=inf{t≥0|u+X(t)<0}。相应的最终破产概率定义为ψ(u)=P(Tu<∞|U(0)=u)。
我们定义一个随机变量M,M=m如果破产是由第m(m=1,2)个险种的索赔导致的。这样破产概率ψ(u)就可以分解为ψ(u)=ψ1(u)+ψ2(u),这里
ψm(u)=P(Tu<∞,M=m|U(0)=u)(u≥0,m=1,2)
设ω(x),x>0为一非负函数,定义如下折现罚金函数
φm(u)=E[e-δTω( ||U(T)I(T<∞,M=m)|U(0)=u],(u≥0 ;m=1,2)
2 Gerb er-Sh iu折现罚金函的积分微分方程
因为Vi=Vi1+Vi2+…+Vin,其中Vij服从均值为1λj的指数分布,对于时间段Vi。假设0时刻开始时,处于时间段V1中的第 j个小时间段V1j(j=1,2,…,n),称这个小时间段为状态,这样由指数分布,从状态 j转移到 j+1的强度为λj;从状态n转移到状态1的强度为λn。
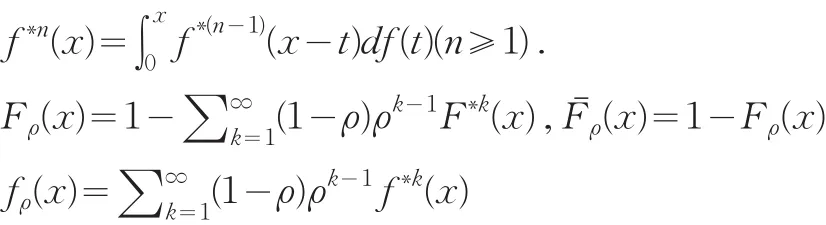
假设φm,j(u)表示处于状态 j时,最终由第m(m=1,2)个险种的索赔导致破产的模型的折现罚金函数。下面推导φm,j(u)所满足的积分微分方程。假设开始处于状态j,j=1,2,…,n-1,对于充分小的时间Δt,我们考虑(0,Δt]内的情况,分成四种:①第二个险种无状态转移,第一个险种无索赔;②第二个险种无状态转移,第一个险种发生索赔;③第二个险种发生状态转移,第一个险种无索赔;④第二个险种状态转移,第一个险种发生索赔。于是有:
化简并利用文献[1]引理6,我们得到:
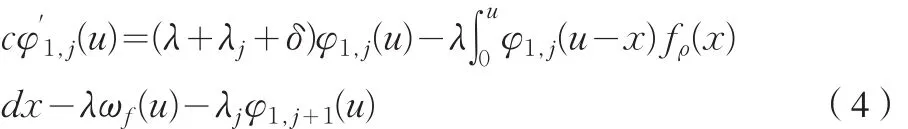
其中:ωf(u)=∫0uω(x-u)f(x)dx
当处于状态n时,我们有:
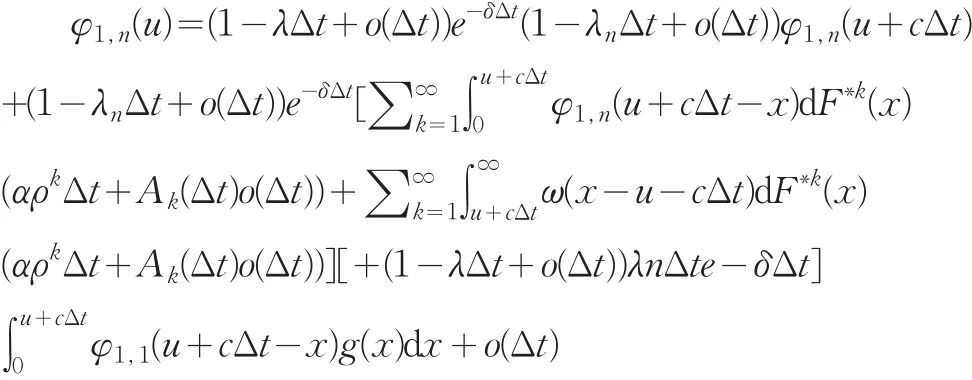
化简得到
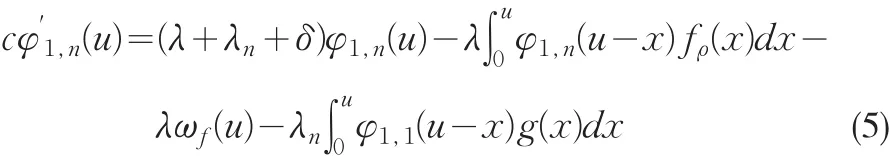
利用同样的方法,我们可以得到:
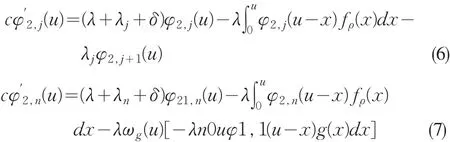
3 Lun d berg方程
记 τ0=0,τk=∑ki=1Vi为第二个险种第k次索赔来到的时刻 ,令 U0=u ,对于 k=1,2,…,Uk=U(τk)=u+cτk-为第二个险种第k次索赔后的盈余过程。下面我们找一个 s使得 {e-δτk+sUk;k=0,1,2…}是一个鞅,容易得到:
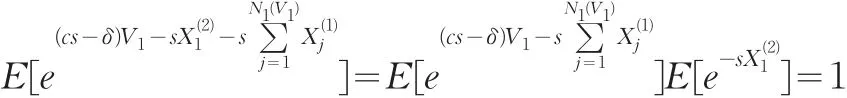
又因为
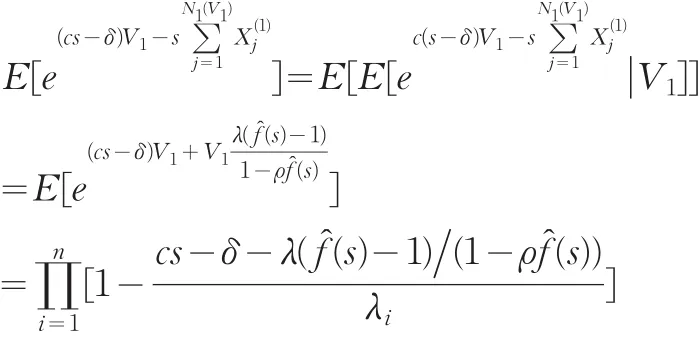
所以鞅条件为:
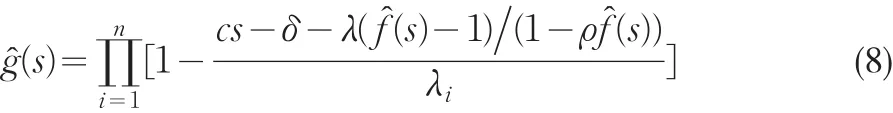
我们把式(8)称为模型(2)的Lundberg方程。容易看出当λ=0,ρ=0 时,式(8)退化为文献[9]中的情况。
定理1 δ>0时式(8)有n个根s1,s2,…,sn,且Re(si)>0。
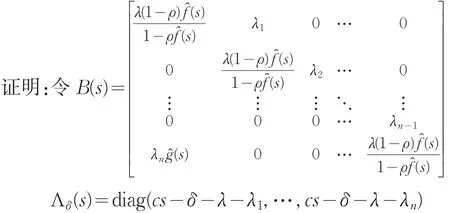
令 Aδ(s)=Λδ(s)+B(s),这样 ||Aδ(s)=0 就等价于式(8)。利用文献[10]、[11]中的方法,令 Aδ(s,u)=Λδ(s)+uB(s),δ>0时,用ς表示半径为R的区域(包括边缘),其中.下面证明,当0≤u≤1时, | Aδ(s,u)|≠0,当s∈ς。因为i=1,2,…,n-1时有:
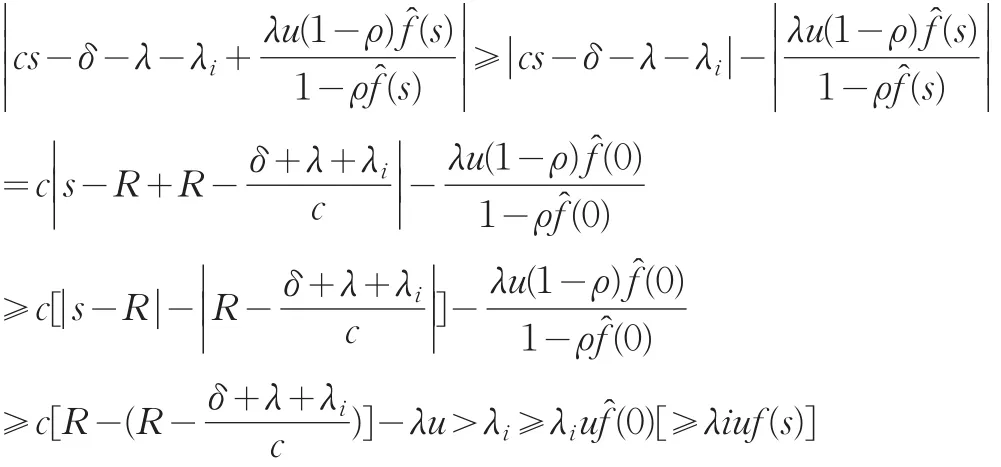
同理i=n时:
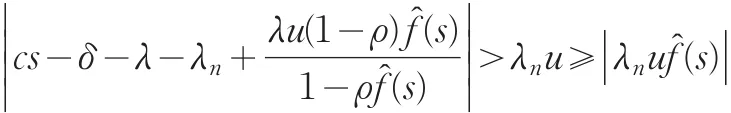
上述不等式表明 | Aδ(s,u)| ≠0,当 s∈ςˉ。具体证明过程参见文献[12]。
下面定义函数 f(u)为 | Aδ(s,u)|=0在区域 ς+(ς的内部)根的个数,这样就有
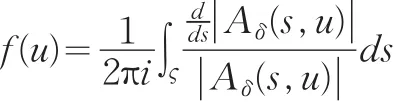
因此,f(u)是[0,1]上的取整连续函数,且为常数。因为|Λδ(s)|=0 有n个根,为。故 f(0)=n。这样就有 f(1)=n。
4 初始资本为0时的Gerb er-Sh iu折现罚金函的精确解
先定义如下的Laplace变换:
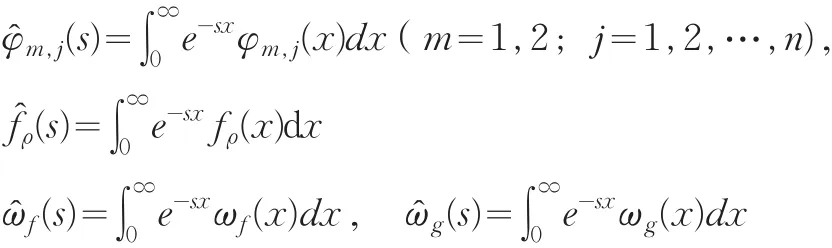
对等式(4)和(5)利用Laplace变换得到:
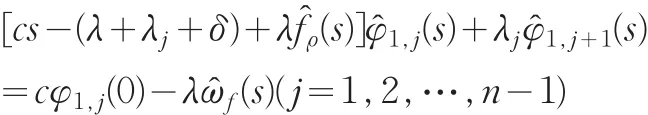
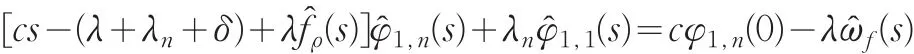
我们记
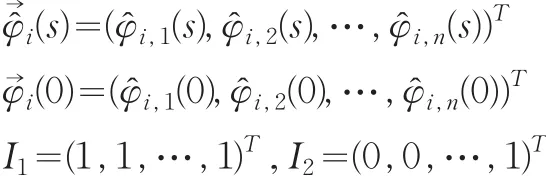
其中I1的n个元素都为1,I2最后一个元素为1,其余为0。又因为
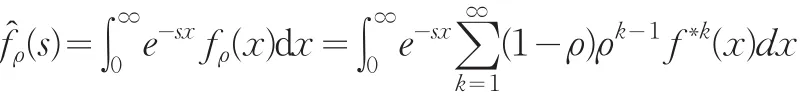
由文献[1]引理6,知上式后一个等式的∫和∑ 交换顺序是可以的。于是
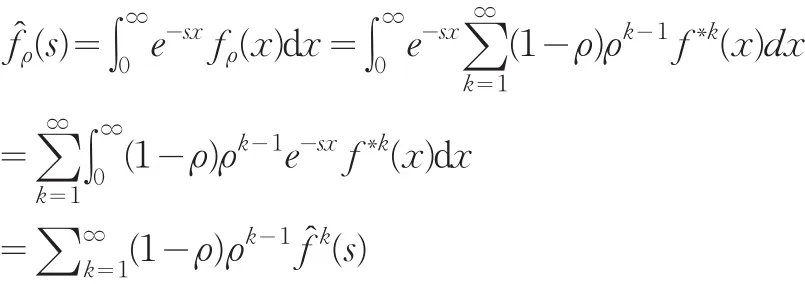
这样上述等式就可以写成如下矩阵形式:
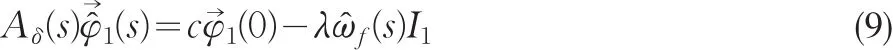
解式(9)得到:
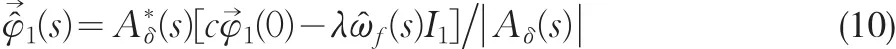
其中,A*δ(s)为 Aδ(s)的伴随矩阵。
同样的,对等式(6)和(7)利用Laplace变换,写成矩阵形式后得到:
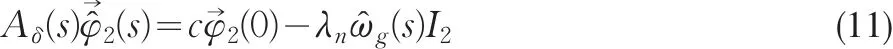
解式(11)得到:
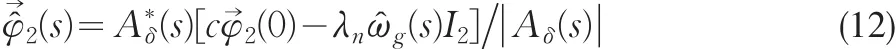
定理2如果(8)式有n个不同的根,则φ1(0),φ2(0)的精确表达式为:

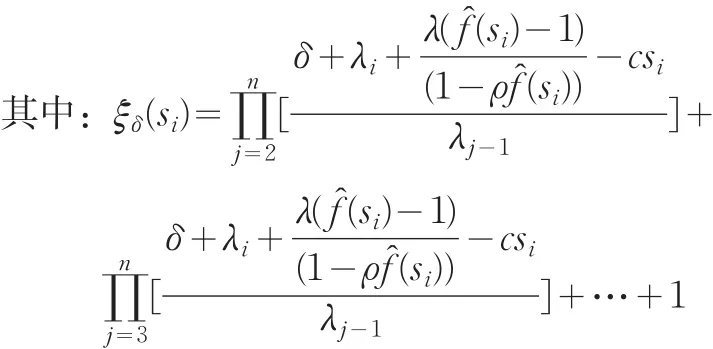
证明:因为 ||Aδ(si)=0(i=1,2,…,n)所以存在非0向量,使得 ATδ(si)=0→ ,将左乘式(9)得到:
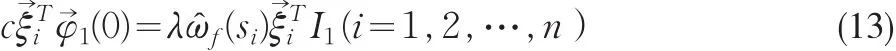
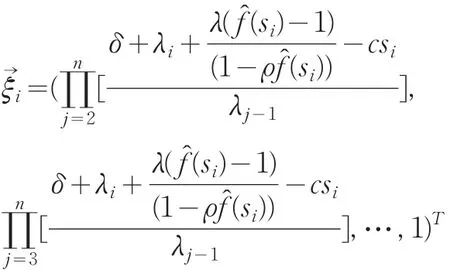

其中, ξδ(si)=ξi1+ξi2+…+ξin(i=1,2,…,n)。利用克莱姆法则有:
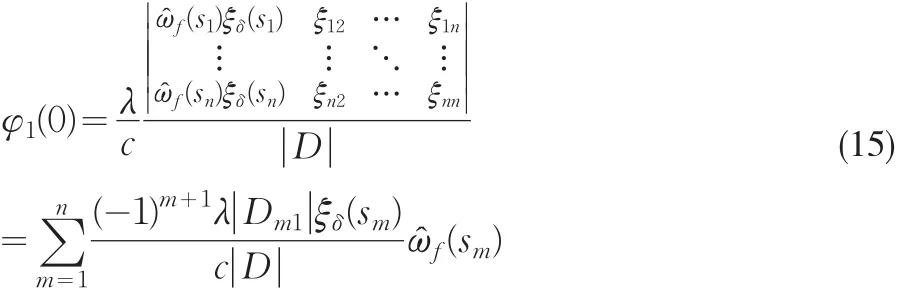
其中,Dm1是矩阵D去掉第一列和第m行后剩下元素组成的矩阵。
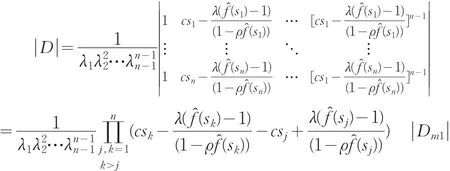
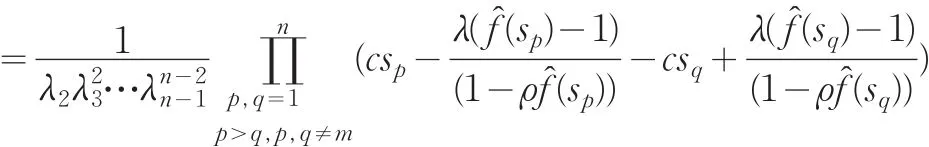
将上面两个展开式代入到式(15)就有:
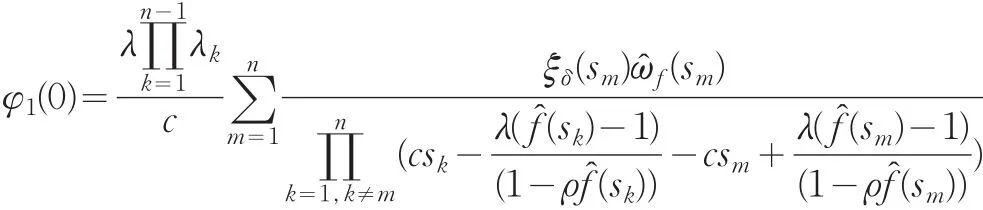
同理可以得到φ2(0)的精确表达式。
[1]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,26(3).
[2]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程下破产概率的显式表达[J].中国管理科学,2007,15(5).
[3]廖基定,龚日朝,刘再明,邹捷中.复合Poisson-Geometric风险模型Gerber-Shiu折现惩罚函数[J].应用数学学报,2007,30(6).
[4]蒋志明,王汉兴.一类多险种风险过程的破产概率[J].应用数学与计算数学学报,2000,14(1).
[5]董亚娟,朱勇华.保险系统中一种推广风险模型的破产概率[J].数学的实践与认识,2004,34(6).
[6]赵晓芹,刘再明.广义二元复合Poisson风险模型破产概率的估计[J].统计研究,2008,25(5).
[7]王晶刚,刘再明,周勇卫.保险系统中一类双险种风险模型的破产概率[J].数学理论与应用,2005,25(1).
[8]赵永霞,尹传存.经典风险模型的推广[J].应用概率统计,2009,25(4).
[9]H.U.Gerber,E,S.W.Shiu.The Time Value of Ruin in a Sparre Andersen Risk Process[J].North American Actuarial Journa,2005,(l9).
[10]de Smit,J.The Queue GI/M/s with Customers of Different Types or the Queue GI/Hm/s[J].Advancesin Applied Probability,1983,(15).
[11]I.Adan,V.Kulkarni.Single-sever Queue with Markov Dependent In Terarrival and Service Times[J].Queueing Systems,2003,(45).
[12]M.Marcus,H.Minc.A Survey of Matrix Theory and Matrix Inequalities[M].Canada:General Publishing Company,1964.

