广东省科技进步对经济增长贡献率的软计算

贺 勇，廖 诺，晋琳琳

（广东工业大学 管理学院，广州 510520）

0 引言

《国家中长期科学和技术发展规划纲要（2006-2020）》中提出“到2020年力争科技进步贡献率达到60%以上”，将科技进步对促进经济增长的作用提高到了前所未有的高度。特别是为确保经济稳定可持续发展，转变经济增长方式，从依靠投资等要素型增长模式转换到依靠科技进步，提高增长效率等质量型增长模式上，对于新的时期，国家或地区科技进步对经济增长的贡献率研究显得尤为重要和紧迫。

在测算科技进步对经济的贡献上取得了大量可喜的成果[1～9]，包括索洛余值法、生产函数法、数据包络法等，但是社会经济系统是一个复杂的非线性系统，并且不同的地区、不同的时期、不同的科技水平，科技进步对经济增长的贡献是不一样的，存在以下问题：第一，在数据的获取和处理上，如何将一个地区的人力资本、技术进步、制度、结构等因素进行量化困难；第二，传统的计算方法，没有考虑各个因素之间的复杂性关系、人们思维的主观性和模糊性以及统计数据的不完整性。第三，没有考虑到各因素对经济发展影响的长期性、间接性和滞后性。

软计算（Soft Computing—SC）[10]是一种新颖的处理复杂经济系统的有效技术，包括人工神经网络、遗传算法和模糊系统等，三种技术相互衔接，既密切的配合又各司其责，联合发挥模式识别、知识推理、优化计算等多种功能，三者互补集成为软计算。软计算方法来测算广东省科技进步对经济增长贡献率的思路是：对广东省21个地区（包括广州、深圳副省级城市及其它19个地级市）按照科技进步水平采用遗传-自组织迭代技术进行软分类；通过模糊神经网络构建物质资本、劳动力、人力资本及研究与开发到经济产出之间模糊映射关系，得到不同科技水平类别的科技进步对经济增长的贡献率；计算广东省及各地区科技进步对经济增长的贡献率。

1 地区人力资本的计算

人力资本分为潜在人力资本和实际人力资本[11]，所谓潜在人力资本是指通过教育、培训、保健等投资支出形成，凝结在劳动者身上由知识、技能、健康等所构成的人力资本。传统的计量方法中主要根据劳动者受教育的程度来计算潜在人力资本。它不仅包括劳动者所具有的人力资本，也包括在校学生、待业人员、退休人员等所具有的人力资本。实际人力资本是指物化在商品与服务中，通过劳动者参加社会经济活动由绩效体现出来的人力资本。考虑到潜在人力资本对经济增长的长期性、滞后性、间接性，这里采用劳动报酬法计算的人力资本是直接作用经济的实际人力资本，使得计算更加符合实际。

按照Byeongju Jeong[12]提出的改进的劳动报酬法来计算，由于地方统计年鉴上没有对各个行业的平均工资数据，用各地区的年最低工资标准来代替各地区未受过教育劳动者的平均工资。根据2001～2009年的《广东统计年鉴》获取相关数据，表1中的第2、6列是人均GDP（单位：万元），第3、7列是当前的年最低工资标准（单位：万元），第4列、第8列是计算得到的广东省各地区的人力资本相对值（以中山市为基准），详细计算方法见文献[13]。

2 对目标系统的软分类

若实际产出为Y，有n个投入要素，则生产函数的一般形式为：

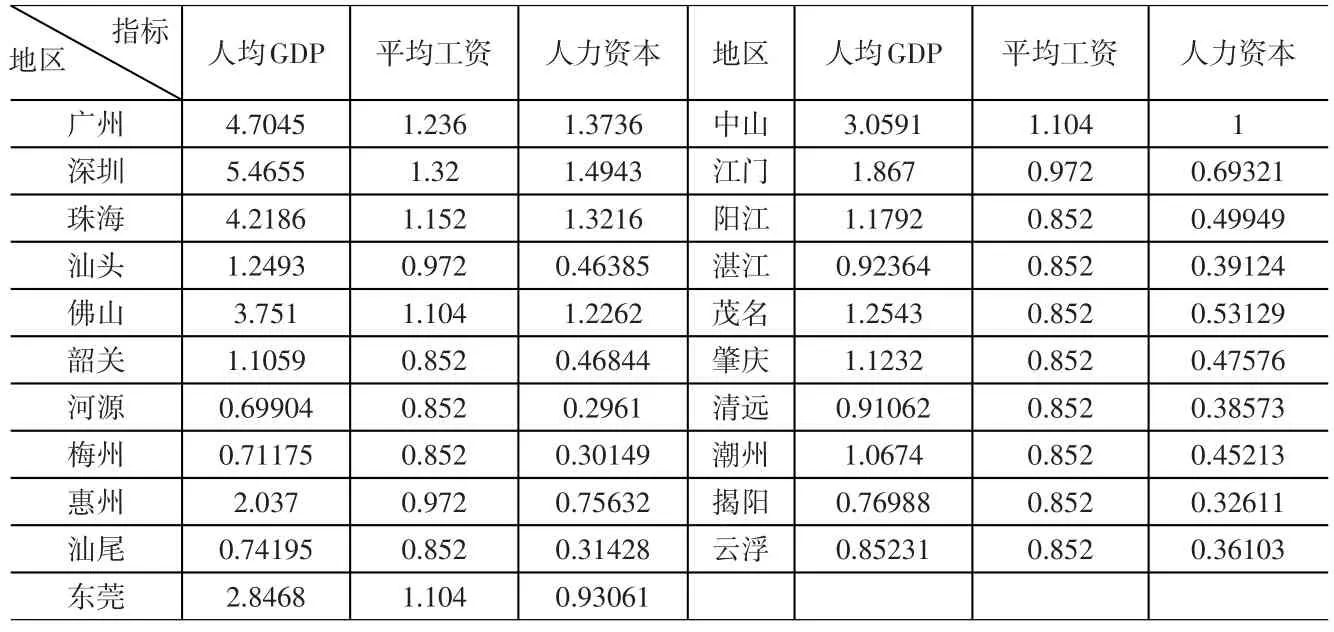
表1 相关数据及计算结果

它代表产出与投入要素之间的某种依存关系。为了实现对广东省21个地区的科技进步水平进行软分类，遵循柯布-道格拉斯（C.W.Cobb-D.H.Douglas）：

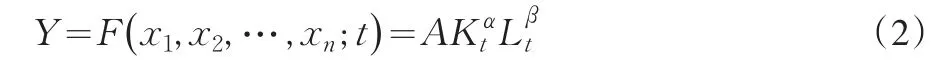
式中α、β是常数，K,L分别代表资本投入、劳动投入，A代表技术进步水平。由（2）式得到：

（3）式表示一个地区的技术进步与该地区的产出、资本投入、劳动投入具有一定的依存关系。基于这种关系，这里科技进步人均产出、固定资产投入和人力资本来衡量，根据2001～2009统计年鉴相关数据进行处理及表1人力资本数据，得到人均产出、人均固定资产投入和人力资本的数据，采用遗传-自组织迭代技术（GA-ISODATA）[14]进行分类，分类结果见表2。

表2 科技进步水平分类

GA-ISODATA分类结果比较好地反映了广东省的经济发展情况。事实上，第一类包含两个广州、深圳两个副省级城市、珠海特区及经济重地佛山，是珠三角的龙头，科技进步水平最高；第二类均为珠三角城市，区位优势突出，经济发展潜力巨大；第三类主要是东西两翼及粤北地区，虽然这些地区之间以及各个地区内部的科技进步有明显差异，但它们都具有农业人口比重大，贫困人口多，科技进步水平整体上偏低。分类结果非常符合广东省的实际情况。

3 模糊系统的实现

为了计算科技进步对经济增长的贡献，在科技进步水平相同的三个子系统内，建立固定资产、劳动力、人力资本及研发投入（R&D）等生产要素到经济增长的的映射，即确定模糊规则中规则前件和后件的参数。表3中第2列是2000～2008年各个地区人均GDP加权平均（单位：万元）；第3列是对各个地区2000～2008年固定资产投入进行折旧后（折旧率5%）的平均值除以期间平均总人口得到的人均固定资产（单位：万元）；第4列地区劳动者人数占全社会总人口的比例；第5列人力资本来自表1的第4、8列的数据；第6列是2000～2008年期间平均每年的人均研发投入相对值（以中山市为基准）。

表3 各地区样本数据表

以表3中各地区的固定资产、劳动力、人力资本、R&D为输入向量，对应的GDP为目标值，构成输入/输出模式，按照神经网络的前向传递与后向调节算法，BP算法[15]）计算得到三条模糊规则，见表4。规则后件的权值bij(i=1,2,3;j=0,1,2,3)描述了三类地区当固定资产、劳动力、人力资本、R&D分别属于规则前件对应的模糊集合时，规则后件的常数项及人均固定资产投入x1、劳动力x2、人力资本x3、研发R&Dx4的系数，表示三类经济系统生产要素对人均GDP的作用大小。图1是网络对21个地区人均GDP的模拟图。

表4 模糊规则参数表（边际贡献）

图1 21个地区GDP模拟图

4 结果分析

根据表4，可对生产要素与经济增长进行下面的分析：

4.1 边际贡献比较

后件参数的每一行反映了对于前件的模糊集合，各生产要素对人均GDP的边际贡献率，例如，第一类表明当固定资产x1∈A11，劳动力x2∈A12，人力资本x3∈A13，R&Dx4∈A14（这里Aij代表中心为aij而宽度为σij的高斯型模糊

集合）时，固定资产劳动力人力资本R&D对人均GDP的贡献率分别是0.466678.452097.423983.702345（见表4），而0.324981归因为制度、结构、区位等其他因素。其它类依此类推。可以看出，GDP对固定资产、劳动力、人力资本及R&D变化率（或者反过来称为边际贡献率）最高的是第一类，即广州、深圳、珠海及佛山，其次是第二类地区；最低的是第三类地区。无论何种生产要素，从边际贡献来看，三类地区呈现明显的阶梯差距。

4.2 贡献份额分析

之和，第8列为2、5、6之和

表5说明，第一类地区经济发展中，固定资产劳动力人力资本R&D对经济增长的贡献份额分别为0.196904.190751.178889.296338，其中R&D最高，可理解为技术创新的力量，为29.63%，，而制度、结构及区位等因素贡献份额为0.137118，科技进步（包括实际人力资本及R&D）的贡献份额为47.52%，在三类地区处于最高水平；全要素生产率（除去物质资本和劳动力作用以外的因素，可理解为广义技术进步）的贡献份额为61.23%。

第二类地区，固定资产劳动力人力资本R&D对经济增长的贡献份额分别为0.123196.214999.282589.144841，而制度、结构及区位等因素贡献份额为0.234376，人力资本在诸多要素中贡献最大，达到28.26%，超过第一类地区中人力资本的作用；但技术创新的力量仅占14.48%，与第一类地区差距很大。科技进步的贡献份额为42.74%，作用次于第一类地区；全要素生产率的贡献份额为66.18%，甚至超过了第一类地区，主要原因是均地处珠三角腹地，区位优势明显，受到广州、深圳及港澳的辐射作用突出。

对于第三类地区，固定资产劳动力人力资本R&D制度、结构及区位对经济增长的贡献份额分别为0.25026.257126.198446.201198.09297，劳动力贡献份额最大，为25.71%，其次是固定资产，为25.03%，而科技进步为39.96%，三类中处于最低水平，由于缺乏制度、结构及区位优势，全要素生产率的份额为49.26%，与一、二类的差距很大。分析说明第一、二类地区已经处于工业化的后、中期，而第三类地区的经济增长对农业的有一定依赖，基本处于工业化的初中期，劳动力及固定资产投资对经济的拉动作用较大。

4.3 科技进步对经济增长贡献率

广东省科技进步对经济增长贡献率：

全省全要素生产率：

表5 各要素对GDP增长贡献份额

其中ωi为第i类地区GDPi占全省GDP的比值，ri为第i类地区科技进步对经济增长的贡献率，r'i为第i类地区全要素生产率。

各地区科技进步对经济增长的贡献率：

其中ti为第i个地区科技进步对经济增长的贡献率，μi为属于第i类的隶属度。

表6 各地区科技进步对经济贡献率

表7 各地区全要素生产率

计算得到各地区科技进步对经济增长的贡献率如表6所示，同理，得到各地区全要素生产率如表7所示。

5 结论

本文对当今社会影响经济增长的主要因素进行了界定，分为三类：要素因素，即物质资本和劳动力；科技进步因素，即人力资本和研发投入；其他综合因素，包括制度、结构及区位等。采用软计算方法，以广东省为例来测算科技进步对经济增长的的贡献率：首先采用改进的劳动报酬法来计算各个地区的人力资本，之后按科技发展水平采用GA-ISODATA对21个地区进行软分类；最后以固定资产、劳动力、人力资本、研发投入为作为模糊神经网络输入，GDP为输出，构建各因素到经济增长的映射关系，通过提取的模糊规则来分析广东省及各地区科技进步对经济增长的贡献率及全要素生产率。研究表明：广东省科技进步贡献率的总体水平为44.02%，全要素生产率为58.71%，结果符合实际，令人信服。

[1]史清琪,秦宝庭.测算技术进步对经济增长的作用[J].科学学研究,1994,(3).

[2]李京文,龚飞鸿,明安书.生产率与中国经济增长[J].数量经济技术经济究,1996,（12）.

[3]周方.“科技进步”及其对经济增长贡献的测算方法[J].数量经济技术经济研究,1997,(1).

[4]宋卫国,李军.“十五”规划我国科技进步贡献率目标选择分析[J].中国科技论坛,2000,(6).

[5]易纲,樊纲等.关于中国经济增长与全要素生产率的理论思考[J].经济研究,2003,(8).

[6]颜鹏飞,王兵.技术效率与生产力增长:基于DEA的实证分析[J].经济研究,2004,(12).

[7]胡宗伟,何大安.科技进步的最优测算方法研究-“兼评solow余值法”[J].科学学与科学技术管理.2005,26(5).

[8]郑京海,胡鞍钢.中国改革时期省际生产率增长变化的实证分析(1979-2001年)[J].经济学(季刊),2005,(4).

[9]陆建芳,戴炳鑫.应用DEA模型分析区域科技进步的相对有效性[J].科技通报.2009,25(3).

[10]J.S.R.Jang,G.T.Sun,E.Mizutani.Neuro-Fuzzy and Soft Computing[Z].A computational Approach to Learning and Machine Intelligence,1997.

[11]石洪华，郑伟.关于人力资本转化模型的探讨[J].科学管 理研究，2004，22.

[12]Byeongju Jeong.Measurement of Human Capital Input Across Countries:a Method Based on the Laborer’s Income[J].Journal of Development Economics,2002,67(2).

[13]贺勇，诸克军.基于软计算的生产要素对地区经济影响[J].系统管理学报，2009,18（3）.

[14]诸克军，成金华，郭海湘.模糊软分类中最佳聚类数的确定[J].管理科学学报，2005，8（3）.

[15]Martin T.Hagan,Howard B.Demuth,Mark Beale.Neural Network Design[M].Cambridge:PWS Publishing Company,1996