复杂曲面CNC加工技术的曲面包络逼近原理*
周凯红 谭湘夫
(①桂林航天工业高等专科学校机械工程系,广西桂林 541004;②湖南理工学院机械工程学院,湖南岳阳 414000)
飞行器机身、机翼覆盖件和推进器叶片等重要零部件都是由空气动力学原理设计的复杂曲面结构。其数控制造技术一直是飞行器制造技术的重要内容[1]。复杂曲面的现代数控制造技术是通过复杂曲面的NURBS离散数据驱动球面刀具相对工件运动实现的。尽管以NURBS法描述复杂曲面的优点已为众多相关研究所证实[2],但是,由其驱动球面刀具完成复杂曲面的数控加工却存在难以接受的缺点:低效率的材料“点”去除加工、高成本的球面刀具。
在多轴联动数控技术出现以前,由于机床加工运动功能的局限性,在刀具相对工件的包络运动中,刀具包络面的特征线(刀刃线)相对刀具是静止的(如仿形法)或沿刀具曲面平动(如范成法),这些都无法充分利用刀具曲面上丰富的曲线去拟合加工目标曲面。在多轴联动数控技术出现以后,由于对直接面向数控加工的曲面逼近理论研究上的不足,通常以NURBS离散数据驱动球面刀具以“点”去除方式来逼近复杂曲面,这实际上是将刀具曲面包络面的特征线(刀刃线)的长度视为零,没有充分利用刀具曲面上的曲线去拟合加工目标曲面。
本文基于微分几何中的曲面活动标架理论提出了一种面向数控加工的曲面逼近理论(包络逼近原理):它以简单(刀具)曲面(如平面、圆柱面、圆锥面和各种螺旋面等)上的定向曲面片(包络面特征线上的微分流形)为基函数,以刀具相对工件的相对运动(变换)形成的包络面按指定的约束条件和精度逼近加工目标曲面,从而获得刀具相对工件的相对运动方程(变换矩阵)。基于包络逼近原理的曲面数控制造技术,其刀具形状是按加工目标曲面设计的简单曲面,其材料去除方式是“线”去除,因而其加工效率较现行球面刀具“点”去除加工方法高,刀具成本低。曲面包络逼近原理也是各种金属切削加工方法的几何学基础。本文将简述曲面包络逼近的数学原理,并通过一个点啮合齿面的曲面构造论证包络逼近原理的应用方法。
1 曲面的包络逼近原理[3]
活动标架的概念起源于研究刚体运动。Darboux[4]等以空间曲线的Frenet标架沿曲线的运动来研究空间曲线的微分结构。E.Cartan[5]将活动标架引入空间曲面的研究,又将其从运动群推广到任意线性变换群,并引进外微分形式,形成研究曲面微分结构的新方法。这一新方法的特点是将曲面微分特性与标架沿曲面的运动联系起来,特别适合描述和控制刀具展成复杂曲面的相对运动。曲面包络逼近原理就是通过刀具曲面与目标曲面活动标架的相对运动关系来描述刀具相对工件的运动,并通过曲面逼近条件来确定刀具与工件的相对运动。
1.1 曲面活动标架下曲面与其包络面的相对运动
如图1,曲面Σ(t)通过相对于坐标系Sp[O(p);x(p)y(p)z(p)]的运动Ψ包络出曲面Σ(g)。设Lp是曲面Σ(g)上的一条曲线,Lt是曲面Σ(t)上的一条曲线,Lp与Lt对于运动Ψ相互共轭。Lg是形成包络曲面Σ(g)的特征线。因此,在运动的任意时刻,曲面Σ(t)与Σ(g)相切于Lg,而Lg总与Lt和Lp三线交于点M。故在点M对于曲面 Σ(t)与 Σ(g)分别有活动标架 Sft[M;αtvtnt]和 Sfp[M;αpvpnp]。其中,αi(i=t,p)是曲线 Li在点 M 的单位切矢,ni是曲面Σ(i)在点M的单位法矢,vi=ni×αi。另有一曲面Σ(p)与曲面Σ(g)固结且沿曲线Lp与曲面Σ(g)具有二阶切触,图1中未标出。即曲面Σ(g)和曲面Σ(p)沿曲线Lp二阶及二阶以下参数均相等。曲面Σ(t)相对曲面Σ(g)的角速度为
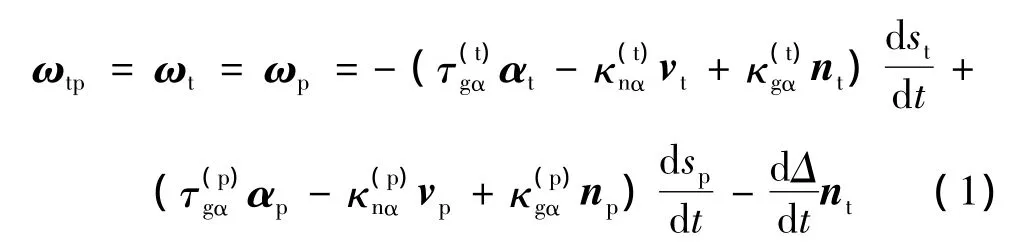
在M点曲面Σ(t)相对曲面Σ(g)的速度为
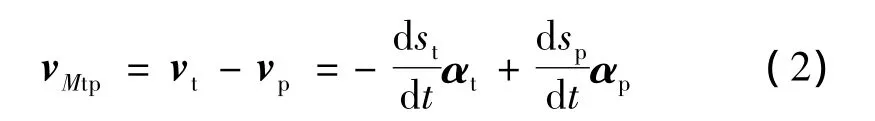
因此,在任意点点曲面Σ(t)相对曲面Σ(g)的速度为
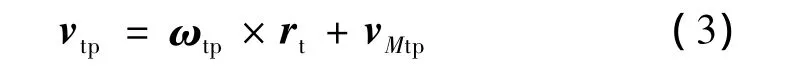
这里:dsp/dt=|driM/dt|(i=t,p)是点M在曲面Σ(i)上沿曲线Li运动的速率;riM是曲线Li上啮合点M的位置矢量;τ(i)gα、κ(i)nα分别是曲面 Σ(i)在点 M 沿 αi方向的短程挠率和法曲率,κ(i)gα是曲面 Σ(i)在点M 沿 αi方向的短程曲率;rt是曲面Σ(t)任意一点的位置矢量。
于是,曲面Σ(t)的包络运动Ψ被表示为曲面Σ(t)和Σ(g)及其各自曲面上的曲线的微分几何(活动标架运动)参数及两曲面活动标架的相对位置参数的函数。实际上,运动Ψ也代表一种从曲面Σ(t)到曲面Σ(g)的运动变换。如果曲面Σ(t)是一种曲面结构比较简单的刀具曲面(如平面、圆柱面、圆锥面和各种螺旋面等),那么,通过控制这种变换就可能包络出结构复杂的曲面Σ(g)使其以最小的误差逼近一个加工目标曲面。这就是包络逼近原理。
1.2 从曲面Σ(t)到曲面Σ(g)的运动变换及曲面Σ(g)的方程
为了实现上述最小误差逼近,有必要写出包络运动Ψ的变换矩阵和曲面Σ(g)的数学表达式,以便建立这种最优曲面逼近模型。
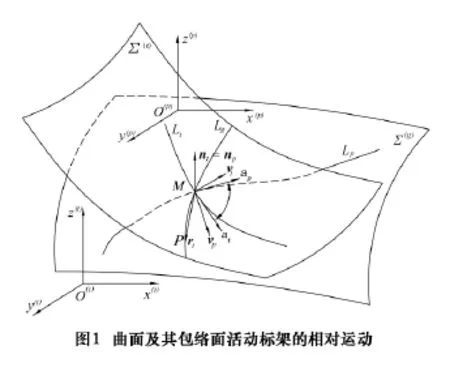
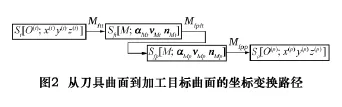
由图1可知,从曲面Σ(t)到曲面Σ(g)的坐标变换路径如图2所示。因此,从曲面Σ(t)到曲面Σ(g)的变换矩阵为
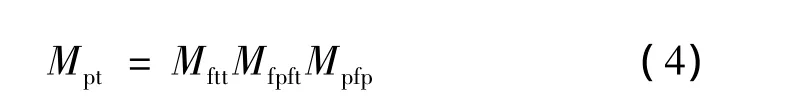
其中:

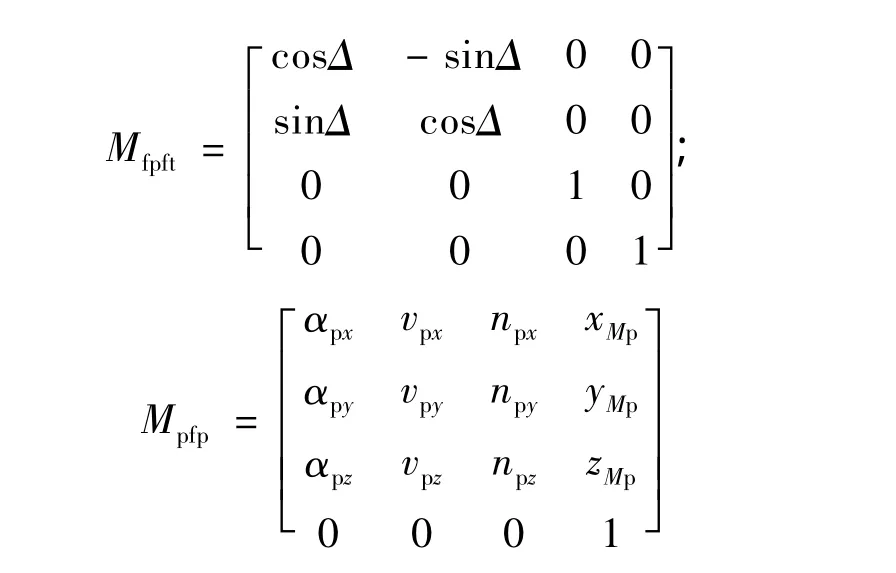
曲面Σ(t)的包络面Σ(g)的方程
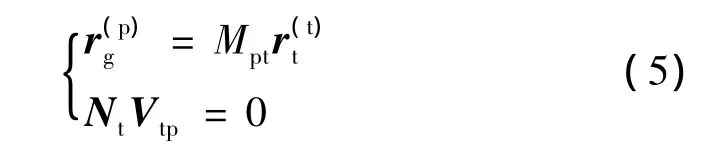
由式(4)、(5)的分析可知,式(5)所确定的包络面Σ(g)的方程是由曲面Σ(t)、曲线Lp与Lt的相应参数及Δ来描述的。如果我们把包络面Σ(g)上的曲线Lp作为Σ(g)逼近目标曲面Σ(p)的约束条件,则通过控制Δ函数可以得到适当的包络运动Ψ,使包络面Σ(g)在曲线Lp以外的区域逼近Σ(p)
1.3 曲面Σ(t)的包络面Σ(g)逼近目标曲面Σ(p)
如图3,包络面Σ(g)以曲线Lp为约束条件逼近曲面 Σ(p),即 Σ(g)可以与 Σ(p)相交(或相切)于 Lp。Lg是组成Σ(p)的过Lp上任意点M的包络特征线,点和是Lg的两个端点,Qg是Lg上这两个端点之间的任意一点。Qg与它在目标曲面Σ(p)上的对应点Qp由图3所示来确定。故曲面Σ(g)在其任意点与目标曲面Σ(p)的偏差δ表示为
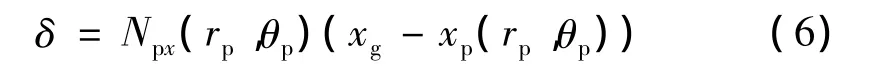

沿Lg各点以两端点N(1)k和N(2)k所对应的偏差和最大,只有同时控制和,才能保证曲面Σ(g)逼近目标曲面Σ(p)的精度。故包络面Σ(g)逼近目标曲面Σ(p)的最优模型:
目标函数为

约束条件为

约束条件式(8)保证曲面Σ(g)从目标曲面Σ(p)的外侧逼近目标曲面Σ(p)。式(7)中的ε是预定的曲面逼近的误差。当+的最小值不能满足式(7)时,一般有两种方法进行改进:(1)根据目标曲面Σ(p)的形状重新选择或设计刀具曲面Σ(t)。(2)缩小包络逼近的区域,即减小端点N(1)k和N(2)k离开点M的距离。通过求解由式(7)和(8)构成的优化模型可以确定Δ函数,从而由式(3)和(4)得到刀具相对工件的运动方程和变换矩阵。将这个运动方程和变换矩阵在多轴联动数控机床上等效实现,就可在数控机床上完成用刀具Σ(t)对目标曲面Σ(p)的“线”去除加工。
2 曲面的包络逼近原理在点啮合齿面展成上的应用实例
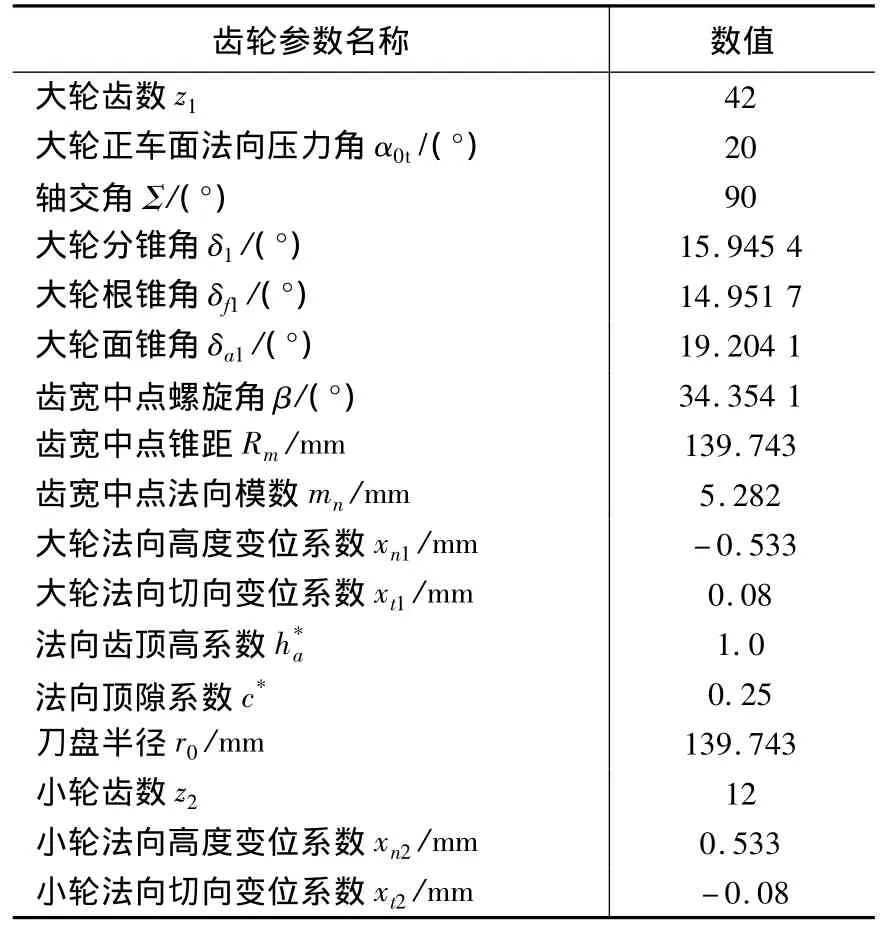
表1 齿轮副主要几何参数表
弧齿锥齿轮副是一种航空领域常用的高速重载动力传动的点啮合齿面传动。传动过程中啮合点在齿面上的轨迹就是接触迹线。在这种齿轮副中,大轮齿面一般是由成形法加工得到的圆锥面,而小轮齿面与大轮齿面配对啮合必须满足多种啮合特性,一般是复杂曲面。但展成这种小轮齿面的刀具曲面仍是简单的圆锥面。本例依据曲面的包络逼近原理,通过刀具圆锥面Σ(t)运动产生的包络面 Σ(g)逼近这种复杂曲面Σ(p)。这里,曲面逼近的约束条件就是包络面Σ(g)沿齿面接触迹线Lp与Σ(p)具有二阶切触。
表1是所研究齿轮副的安装传动的主要几何尺寸。表2是齿面接触迹线Lp的离散点坐标及其对应的主曲率。小轮的理论齿面Σ(p)就是大轮齿面在上述齿轮副安装传动条件下的包络面。
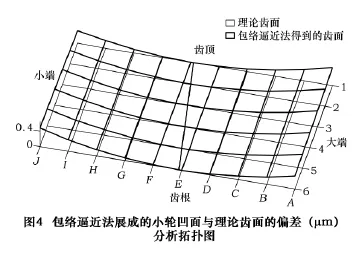
图4是包络逼近法展成的小轮凹面与理论齿面凹面的偏差分析拓扑图。图中数据表明实际加工得到的齿面与理论齿面沿接触迹线Lp相切,且在远离接触迹线的齿面边缘,与理论齿面的最大偏差只有0.45 μm,这表明只要根据加工目标曲面的形状设计适当的刀具曲面,按包络逼近法展成的曲面可以在一定曲面范围内以很小的误差逼近目标曲面。图5是按包络逼近法在UG中构造的小轮齿槽三维实体。


表2 齿面接触迹线上部分点的主曲率及坐标
3 结语
本文论述的曲面包络逼近理论是以材料的“线”去除方式加工复杂曲面的CNC制造技术的几何学基础,是直接面向数控加工的曲面逼近理论。由于该方法以“线”去除方式加工复杂曲面,因此,比以往的材料“点”去除加工方法加工效率要高。实例计算表明:只要根据加工目标曲面的结构设计刀具曲面,由包络逼近原理加工目标曲面就能达到足够的加工精度要求。
[1]张耀.航空科学技术的发展[M].北京:航空工业出版社,2007:129-133.
[2]朱新雄,等.自由曲线曲面造型技术[M].北京:科学出版社,2003:138-168.
[3]周凯红.基于预定啮合特性的螺旋锥齿轮点啮合齿面设计及CNC制造技术研究[D]长沙:中南大学,2009.
[4]Pogorelov A V,Differential geometry[M].Netherlands:Noordhoff,Groningen,1958:38-41.
[5]O’Nell B.Elementary differential geometry[M].New York:Academic Press,1966:52 -56.

