基于FTS的非轴对称微结构表面超精密切削系统研究*

王晓慧 孙 涛

(哈尔滨工业大学精密工程所，黑龙江哈尔滨 150001)

微结构表面是指具有特定功能的微小拓扑形状的表面，其特征尺寸一般不大于微米级。这些微小拓扑形状具有高度规则的结构特征，这些特征与传统的表面参数及统计特征不同，它们一般都有很大的深宽比。这些表面结构使得元件表现出某些特定的性能，如光学性能、粘附性、摩擦性、润滑性和耐磨损性等［1］，并且能够实现普通元件难以实现的阵列、微小、集成、成像和波前转换等新功能，因此被广泛应用于光束整形、光学器件互连、三维成像与探测等领域［2］。随着高精度、高刚度的空气静压主轴和精密伺服机构的出现，使得利用超精密车削加工技术来加工具有微三维结构表面的元件成为可能，并逐渐成为微制造领域中的一个非常重要的研究方向。对于非轴对称微结构的金刚石车削加工来说，机床不仅需要具有多自由度即高次轨迹联动控制能力，还需要具有良好的高频动态响应性能和很高的分辨率，传统的多轴联动机床很难满足其要求。近几年来，随着驱动技术和控制技术的发展，出现了快速刀具伺服技术(Fast Tool Servo，FTS)［3］，这种加工方式是利用2个直线轴X、Z，以及1个旋转主轴，通过为主轴的转动角度添加反馈与控制手段，突破了在3轴车床上加工非轴对称微结构等自由曲面的限制。

由于压电陶瓷具有分辨率高、响应快、刚度大等优点，成为常用的FTS驱动元件，但是压电陶瓷本身所固有的迟滞、蠕变等非线性特点不但会降低FTS系统的控制精度，而且可能造成系统失稳［4－5］。近年来，针对精密制造系统中迟滞非线性的控制日益成为各国学者关注的焦点。A.Main John等通过PD反馈控制来提高压电陶瓷执行器的动态响应速度［6］。Ge将前馈静态迟滞补偿与常规PID控制相结合，应用到压电执行器跟踪系统中［7］，但是，该方案仅对周期性输入信号有效。Hwang利用两个结构相同的神经网络分别建立单环迟滞的上下半环逆模型，然后结合变结构控制方法对迟滞系统进行控制［8］，但是其建立的逆模型仅仅针对于单环迟滞现象，并不适用于多环迟滞系统的控制。尽管上述不同的控制技术可以在一定程度上补偿压电陶瓷本身的迟滞非线性效应，但大都是针对周期性驱动信号的情况。在复杂微结构表面的加工中，快速伺服刀架的切削深度与切削频率是随着微结构表面的轮廓实时变化的，因此，针对FTS的动态迟滞特性，本文建立了基于拓展输入空间法的FTS神经网络逆模型，并将该逆模型作为PID控制的前馈环节，实现FTS的闭环复合控制。最后，我们利用FTS系统成功实现了典型非轴对称结构正弦网格微结构表面的加工。

1 快速伺服刀架及其运动控制

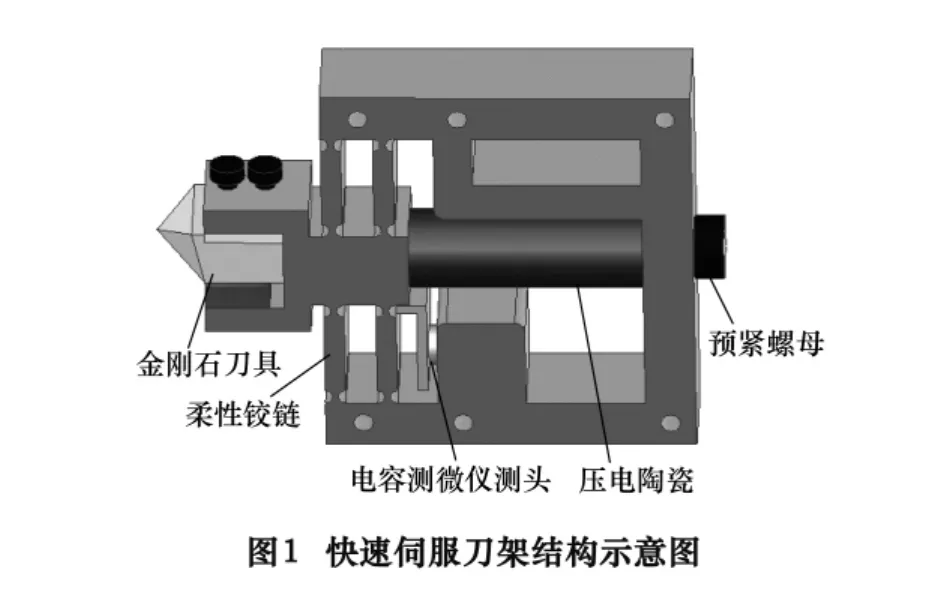
作为微结构表面加工系统的关键部件，FTS的具体结构如图1所示。选用德国PI公司的P－841.20型压电陶瓷微位移器作为FTS的驱动元件，其最大伸长量为30 μm，分辨率可达0.3 nm，采用电容测微仪检测刀具的实时位移。

FTS在开环状态下其升压位移曲线与降压位移曲线并不一致，同样的输入电压因为加压历史的不同对应不同的输出位移，同样的输出位移对应不同的输入输出曲线，而且其迟滞曲线宽度随着输入电压幅值的增加而增大，见图2a。FTS动态迟滞非线性特点体现在其驱动电压速率依赖性(Rate－denpendence)上，改变输入信号频率，幅值60 V，输入频率分别为0.1 Hz、1 Hz、2.5 Hz、5 Hz，测试其输入输出特性，如图 2b 所示。随着输入电压频率的改变，FTS迟滞曲线的形状和宽度也随之改变。随着输入电压信号频率的增加，其最大输出位移值也随之变小，频率为0.1 Hz输入信号的最大输出位移比频率为5 Hz输入信号的最大位移大0.2 μm左右;同时，随着输入信号频率的增加，其迟滞曲线的宽度也略有增加。

由此可见，FTS的输出位移不仅与当前输入电压和历史输入电压有关，还与输入电压信号的频率有关，其动态迟滞特性是典型的具有记忆性且多对多的非线性映射问题。因此，建立能够描述其动态迟滞特性，并具有常规逼近技术优点的新方法是本文的研究。

对于迟滞非线性系统，目前采取的主要是基于系统逆模型的控制策略。为了能够建立准确的迟滞逆模型实现对迟滞系统的非线性补偿，构造1个基于神经网络的迟滞逆模型是一个有效的方法。由于迟滞逆的输入与输出之间是一种多值映射关系，不能够直接利用神经网络来逼近迟滞逆系统，因此，我们通过引入1个迟滞逆算子，将迟滞逆的多值映射关系转变为一对一的映射关系，进而利用神经网络来建立FTS系统的逆模型。迟滞逆算子的数学表达式为

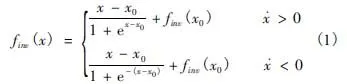
式中，x为当前输入;finv(x)为当前输出;x0为与当前输入相邻的先前输入极值;finv(x0)为当输入为x0时的输出极值。

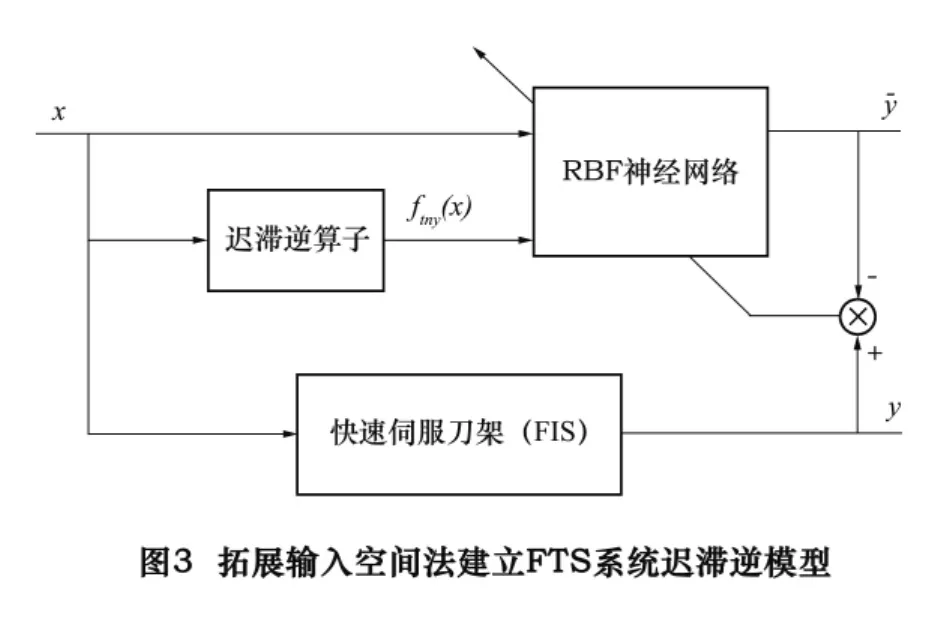
我们将迟滞逆算子的输出finv［x(t)］与FTS系统的位移x(t)一起作为神经网络的输入向量，这样神经网络的输入空间就由原来的一维增加到了两维，我们称之为输入空间的拓展。这样，我们就可以在多维空间中唯一地确定迟滞特性的每一个状态，建立FTS的迟滞逆模型。由于径向基函数(RBF)神经网络具有计算量小、收敛速度快、无局部极小等优点，因此本文利用RBF神经网络作为迟滞逆非线性系统的建模工具，建立的迟滞逆模型结构如图3所示。

模型误差带来的影响，控制系统框图如图4所示。首先由建立的神经网络系统逆模型根据指令位移xi(KT)给出基本控制电压ui(KT)，然后比较指令位移xi(KT)与实际位移x(KT)的差e(KT)，该误差经PID反馈控制器运算后得到调整量Δu(KT)，用来补偿逆模型误差及外界不确定因素扰动。

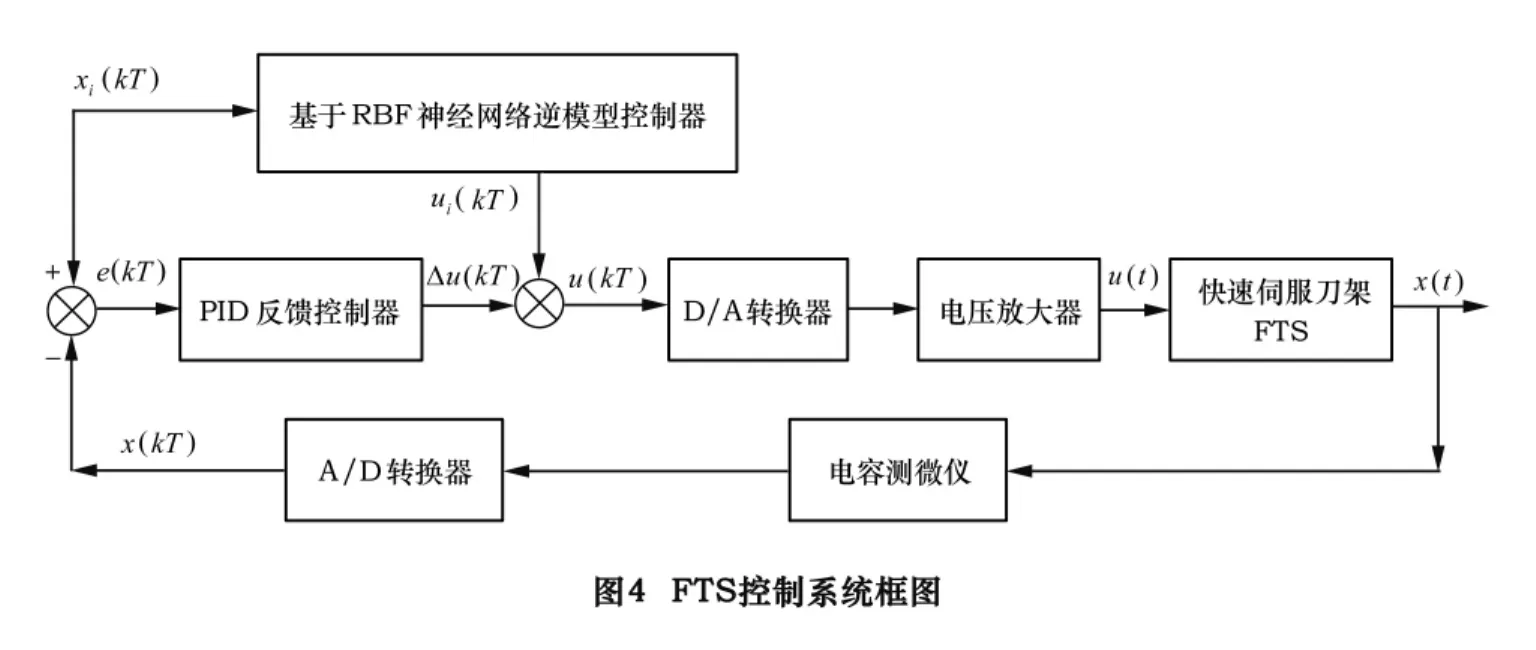
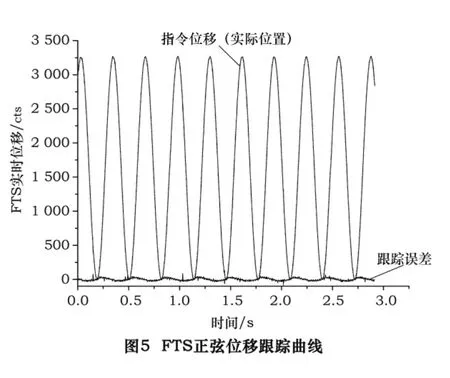
图5为快速伺服刀架加工过程中实测的正弦位移跟踪曲线，利用上述控制策略，FTS系统的跟踪误差减小到150 nm以内。1 cts约等于2 nm。

2 微结构表面加工实验

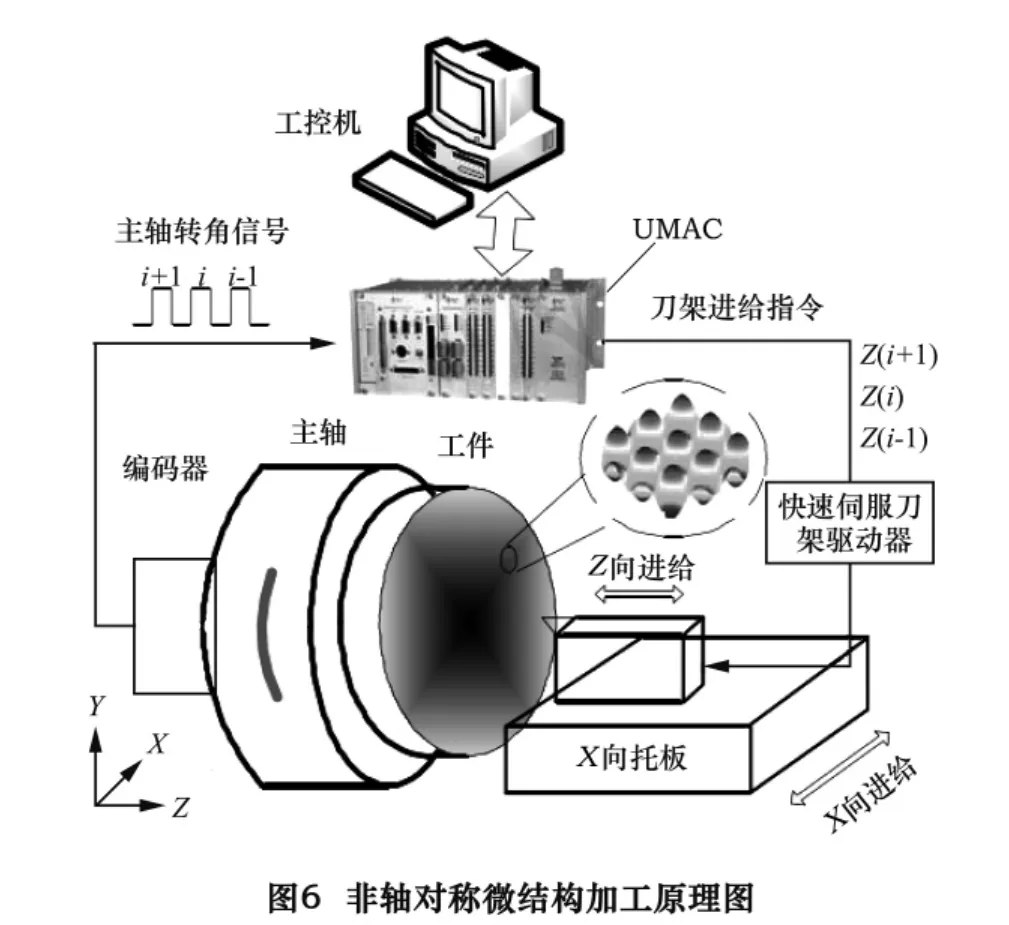
为了验证上述FTS控制策略的有效性，我们进行了非轴对称微结构表面的加工实验。加工过程中工件装夹在主轴上随主轴旋转，X向进给由X向拖板实现，Z向进给则由安装在X向拖板上面的快速伺服刀架来完成。对于非轴对称微结构表面的加工需要X、Z轴和主轴转角θ三个坐标联动，即Z向进给不仅和X向位移还要和主轴转角θ成一定的函数关系，加工原理图如图6所示。设主轴转速为T，主轴编码器每转一圈的脉冲数为P，X导轨的进给速度为F，则第i个主轴编码器脉冲对应的加工点的位置利用极坐标可表示为

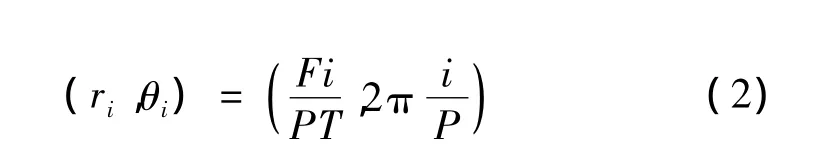
该点对应的切削深度z(i)为

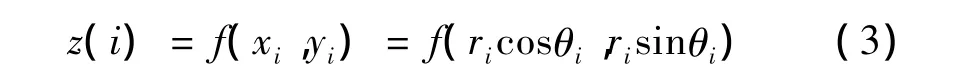
图7是利用Taylor Hobson白光干涉仪检测的所加工正弦网格微结构表面的三维形貌，该微结构表面在X向与Y向均为波长1 mm，峰谷值为10 μm的正弦波。

3 结语

本文介绍了基于快速伺服刀架的微结构表面车削加工系统，并针对快速伺服刀架的迟滞非线性特点，采用拓展输入空间法建立了其神经网络逆模型，并将该逆模型应用到PID闭环反馈控制中，大大提高了FTS的动态跟踪性能。最后，利用该加工系统成功实现了典型非轴对称结构正弦网格微结构表面的车削加工。

［1］P Sandoz，B Trolard，D Marsaut，et al.Micro－structured surface－ element for high－accuracy position measurement by vision and phasemeasurement［C］.Proceeding of the Society of Photo － Optical Instrument Engineers.Strasbourg，France，2004:606 －610.

［2］M Wech，S Fischer.Manufacturing of microstructures using ultraprecision machine tools［C］.Part of the Symposium on Design，Test，and Microfabrication of MEMS and MOEMS.Paris，France，1999:450 －455.

［3］Gao Wei，Jun Aoki，Bing － Feng Ju，et al.Surface profile measurement of a sinusoidal grid using an atomic force microscope on a diamond turning machine［J］.Precision Engineering，2007，31(3):304 －309.

［4］Ge P，Jouaneh M.Modeling hysteresis in piezoceramic actuators［J］.Precision Eng，1995，17(3):211 －232.

［5］Li Chuntao，Tan Yonghong.A neural networks model for hysteresis nonlinearity［J］.Sensors and Actuators，2004，7112(3):49 －54.

［6］A Main John，Garcia Ephrahim.Piezoelectric stack actuator and control system design:strategies and pitfalls［J］.Journal of guidance，control and dynamics，1997，20(3):479 －485.

［7］Ping Ge，Musa Jousaneh.Tracking control of a piezoceramic actuator［J］.IEEE Trans.Control System Technology，1996，3(4):209 －215.

［8］Chih－Lyang Hwang，Chau Jan，Ye－Hwa Chen.Piezomechanics using intelligent variable － structure control［J］.IEEE Trans.Industrial Electronics，2001，48(1):47 －59.