具有A.K.Fung海谱的粗糙海面电磁散射的微扰法研究

田炜，任新成，黄保瑞

（延安大学物理与电子信息学院，陕西 延安716000）

具有A.K.Fung海谱的粗糙海面电磁散射的微扰法研究

田炜，任新成，黄保瑞

（延安大学物理与电子信息学院，陕西 延安716000）

运用微扰法研究了平面电磁波入射随机粗糙面的电磁散射问题，得到了具有A.K.Fung海谱的粗糙海面散射截面的数学表达式，进一步得出了不同极化状态下散射系数的计算公式。通过数值计算得到了双站和单站两种情形下散射系数随散射角、风速、入射波频率变化的曲线，讨论了粗糙面高度起伏均方根、海水温度、风速、入射波频率对散射系数的影响，得出了具有A.K.Fung海谱的粗糙海面散射系数的特征。数值计算结果表明粗糙面高度起伏均方根、海水温度、风速、入射波频率对散射系数影响是比较复杂的。

电磁散射；微扰法；A.K.Fung海谱；散射系数

Abstract: The electromagnetic scattering from random rough sueface with plane electromagnetic wave incidence is studied using the Small Perturbation Method, and the mathematical expression of radar cross section of rough surface with A.K.Fung spectrum is derived , and the formulae of the scattering coefficient for different polarization is obtained.The curves of the scattering coefficient of mono-scattering and bistatic scattering with varying of the scattering angle,wind speed and the frequency of the incident wave are obtained by numerical implementation.The influences of the root mean squre, the temperature of seawater, wind speed and the frequency of the incident wave on the scattering coefficient are discussed, and the characteristics of scattering coefficient from rough surface with K.Fung spectrum is obtained.The numerical results show that the influences of the root mean squre, the temperature of seawater, wind speed and the frequency of the incident wave are very complex.

Keywords: electromagnetic wave scattering; the Small Perturbation Method; A.K.Fung sea spectrum; the scattering coefficient

近几十年来，粗糙面散射一直是一个十分活跃、有着大量实际应用、且为许多学科领域共同研究的热门课题[1-5]，如海面通信会受到粗糙面散射的影响，无线电海洋学中，根据雷达接收的散射波来识别海上或海面附近的目标；红外、可见光遥感中，利用目标对光波的散射获得数据以识别目标形态和特征，再如对人体组织的超声波散射，粗糙金属表面的光学散射等方面均用到粗糙面散射理论。另外，有关粗糙面散射理论在军事跟踪、制导、水下声学、雷达目标成像、军事装备隐身、固体物理、辐射测量学和天文学等领域都有广泛的应用。

在以往的粗糙海面散射研究中，利用近似解析方法和数值方法研究粗糙海面散射、粗糙海面与目标的复合散射居多[6-13]，较少涉及运用近似解析方法研究海面风速、入射波频率对粗糙海面散射特性的影响问题。本文基于微扰法[5,6]推导了平面电磁波入射随机粗糙面的散射截面计算公式。实践证明：该微扰法物理思想明确，避免了繁琐的推导和证明，能十分有效地解决粗糙面散射问题。并据此研究了具有A.K.Fung海谱的粗糙海面电磁散射问题，本文结合A.K.Fung海谱[4]，推出了不同极化状态散射系数的数学表达式，通过数值计算得到了双站和单站两种情形下散射系数随散射角的变化曲线，讨论了粗糙面高度起伏均方根、海水温度、风速、入射波频率对散射系数的影响。

1 理论基础

■→

1.1 散射问题的公式

假设有一水平极化平面波入射到微粗糙界面上，如图1所示，并假定界面可用随机函数来描述，它的傅里叶变换对为：

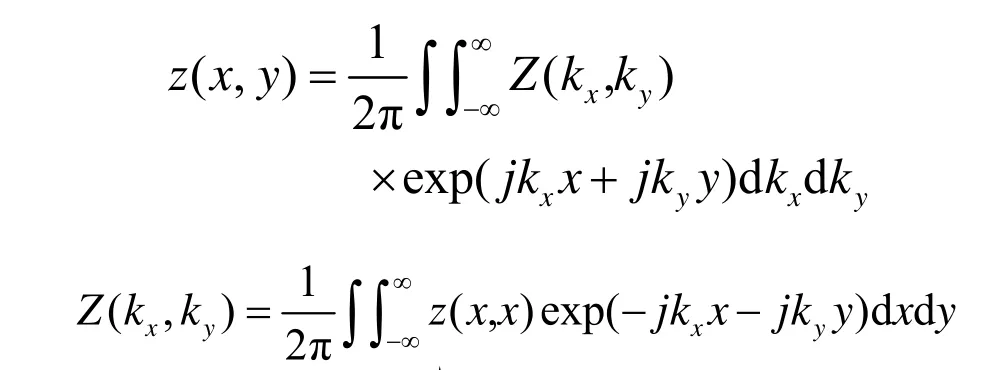
图1 粗糙面电磁散射问题几何示意图Fig.1 Geometry of the electromagnetic wave scattering from rough surface

假设介质1和介质2中的散射场是从界面传出的。入射场取水平极化平面波，在xz平面内传播。于是，介质1中的总电场是入射场加上相干和非相干散射场之和。

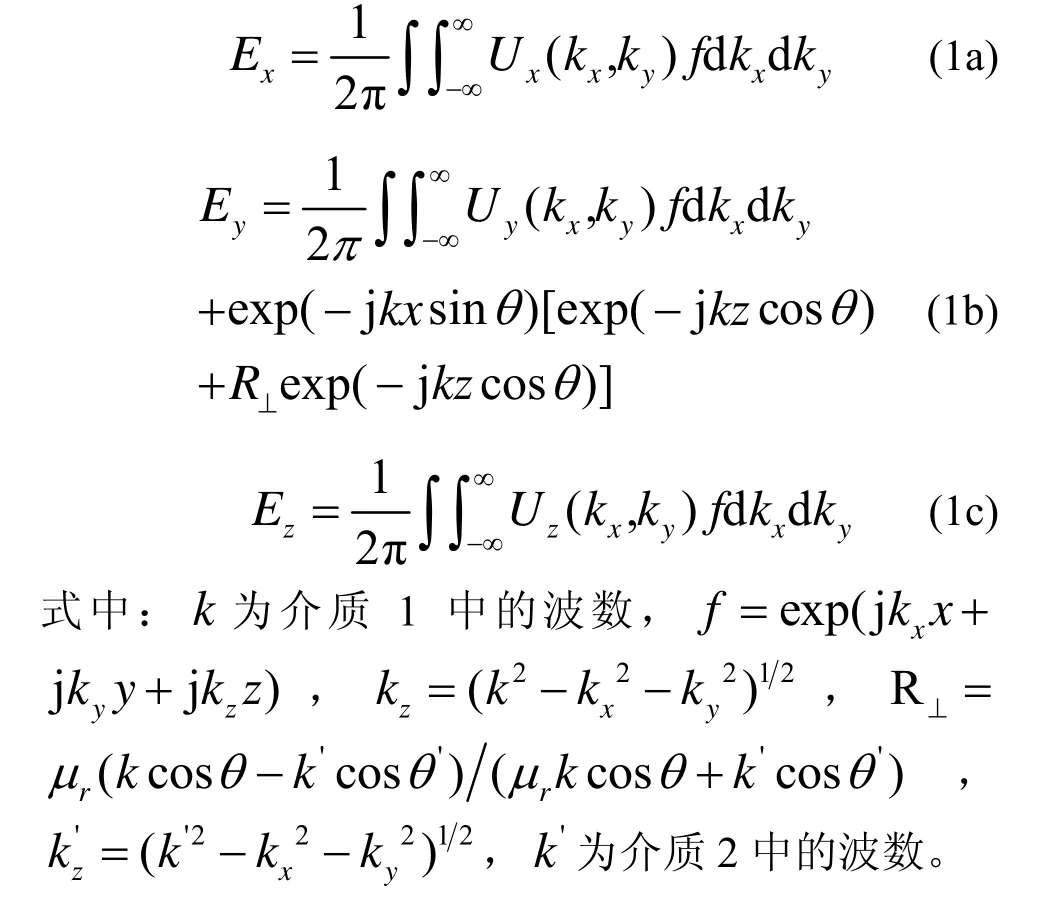
1.2 场强幅度的确定

式(1a)、(1b)、(1c)中的未知场强幅度可以通过边界条件和散度关系来确定，边界条件为：

1.3 极化幅度

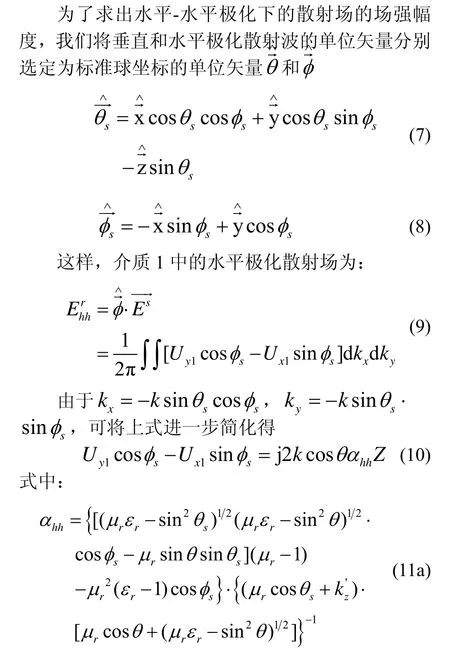
上式提供了水平-水平极化下的极化幅度，考虑到存在对偶性，因此垂直-垂直极化下的极化幅度可由rμ和rε互换的方法来求出，即

1.4 散射系数

2 具有A.K.Fung海谱的粗糙海面散射系数公式

根据微扰法理论，将(12)式、(23)式代入式(22)，可得经过粗糙海面散射的电磁波单位非相干双站散射截面，同理，将(25)式、(23)式代入式(22)，可得经过粗糙海面散射的电磁波单位非相干单站散射截面，这样就可以得到粗糙海面电磁波的散射系数如下

3 数值计算结果和讨论

3.1 双站情形

对于双站情形，首先研究在入射波频率f、入射角θi一定时，双站散射系数σ随散射角 θs的变化规律及粗糙面高度起伏均方根δ、海水温度T、风速对散射系数σ的影响；其次研究在入射角θi、介质介电常数ε、入射波频率f一定的条件下，不同散射角θs、不同极化情形下，双站散射系数σ随风速u的变化规律；最后研究入射角θi、散射角θs、风速u、海水温度T一定时，不同极化状态下，散射系数σ随入射波频率f的变化规律。在下面计算过程中若不特殊说明，选用平面入射电磁波为I/J波段雷达波，其工作频率为f=10GHz，电磁波入射角取，这是因为微扰法适合于研究较小入射角的粗糙面电磁散射问题。取海水含盐量浓度，选择不同的海水温度T，根据文献[14]计算得到海水的等效介电常数 ε=ε'−ε''i 。

3.1.1 散射系数随散射角变化的数值计算结果及分析 限于篇幅，此处仅考虑HH极化的情形（1）粗糙面高度起伏均方根对散射系数的影响取海水温度计算得到海水等效介电常数研究不同粗糙面高度起伏均方根δ对应的散射系数σ随散射角θs变化的曲线如图2所示。由图2不难看出，在其他参数一定的条件下，在散射角θs变化的绝大部分范围内，粗糙面高度起伏均方根δ每增加一倍，在散射有双站散射系数σ将要增加左右，这一结果在的范围内是近似成立的，但在镜向方向，双站散射系数σ的峰值随几乎不随粗糙面高度起伏均方根δ的变化而变化，这说明在非镜向方向粗糙面高度起伏均方根δ对散射系数σ有较大影响。

图2 粗糙面均方根对双站散射系数的影响Fig.2 Influence of δ on σ

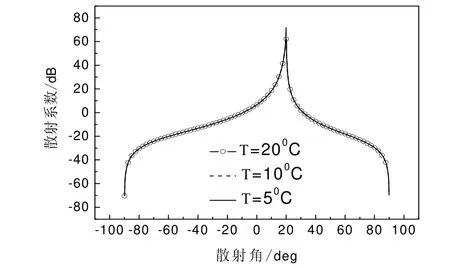
图3 海水温度对双站散射系数的影响Fig.3 Influence of ε on σ

图4 风速对双站散射系数的影响Fig.4 Influence of u on σ

3.1.2 散射系数随风速变化的数值计算结果及分析 此处考虑HH极化和VV极化两种情形，当入射角和散射角一定的条件下，计算散射系数随风速变化的曲线，考虑风速对散射系数的影响。

图5 双站散射系数随风速的变化曲线图Fig.5 Curves of σ with varying of u

3.1.3 散射系数随入射波频率变化的数值计算结果及分析 图6计算了时，在不同极化情形下，散射角sθ分别取（小于入射角），（大于入射角），得出了散射系数σ随入射波频率f的变化曲线，可以看出，在HH和VV极化下散射系数σ随入射波频率f的增大而单调地增大，当入射波频率f时，散射系数σ随入射波频率f增大较快，这一结果对于散射角对应的散射系数σ随入射波频率f的变化曲线尤为明显，当入射波频率f≥35GHz时，散射系数σ随入射波频率f增大较慢，另外，在其它参数一定的条件下，散射角θs取相同值时，HH极化和VV极化条件下散射系数σ随频率 f的变化曲线是分别重合的，并有对应的散射系数大于对应的散射系数。

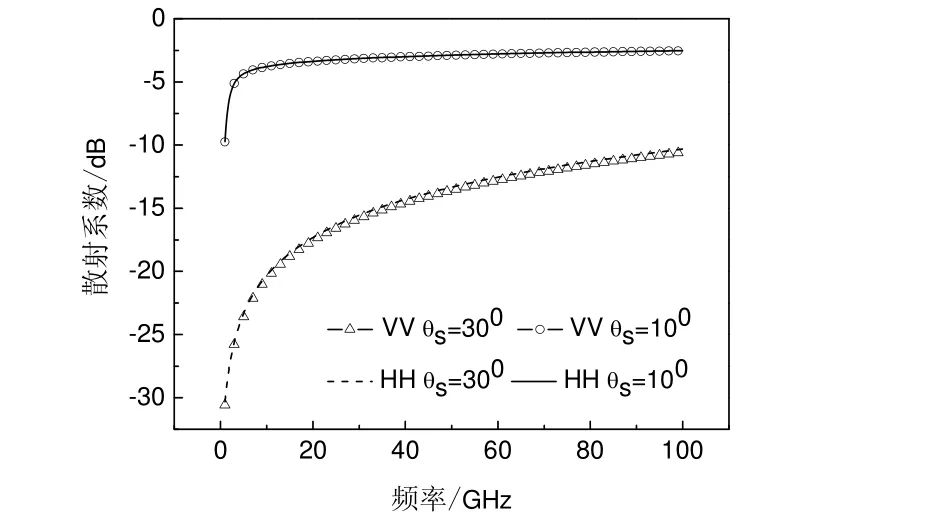
图6 双站散射系数随入射波频率的变化曲线图Fig.6 Curves of σ with varying of f

图7粗糙面均方根对后向散射系数的影响Fig.7 he Influence of δ on σ

3.2 单站情形

3.2.1 后向散射系数随入射角变化的数值计算结果及分析

（1）粗糙面高度起伏均方根对后向散射系数的影响

（2）海水温度对后向散射系数的影响

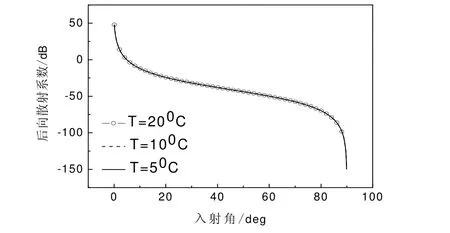
图8 海水温度对后向散射系数的影响Fig.8 Influence of T on σ

数值计算结果表明，VV极化条件下后向散射系数σ随入射角iθ以及随风速变化曲线与HH极化条件下几乎相同，鉴于篇幅该情形下的变化曲线不再画出。

图9 风速对后向散射系数的影响Fig.9 Influence of u on σ

图10 后向散射系数随风速的变化曲线Fig.10 Curves of σ with varying of u

图11 后向散射系数随入射波频率的变化曲线Fig.11 Curves of σ with varying off

3.2.3 后向散射系数随入射波频率变化的数值计算结果及分析 图11给出了的情况下，在不同极化情形下，分别计算了在不同入射角iθ的条件下，后向散射系数σ随入射波频率f的变化曲线，可以看出，在 HH极化和 VV极化条件下，不管入射角后向散射系数σ随风速f增大而单调减小，另外，时，在入射波频率对应相同的情形下，HH极化的后向散射系数σ要比 VV极化的后向散射系数σ大约小时，在入射波频率对应相同的情形下，HH极化的后向散射系数σ将要比VV极化的后向散射系数σ大约小4.0dB左右。

HH极化和VV极化下的后向散射系数σ随入射波频率f的变化曲线是重合的，HH极化后向散射系数小于VV极化的后向散射系数。

4 结 语

本文基于微扰法得到了平面波入射粗糙海面时散射系数的表达式，结合A．K．Fung的粗糙海面海谱的半经验公式导出粗糙面散射系数的计算公式，通过数值计算分别得到了双站和单站两种情形下，散射系数随散射角、入射角变化的基本特性，以及随风速、波长变化的特征。当然本文只研究了一维的情形，有关数值结果有待于进一步实验验证，其它谱分布及二维粗糙面的散射问题还有待于进一步地深入研究。

[1]Ulaby F T, Moore R K, Fung A K.Microwave Remote Sensing [M].London: Addision-Wesbey Publishing, 1982.

[2]Menedez J, Pinczuk A.Light Scattering Determinations of Band Offsets in Semiconductor Heterostructures [J].IEEE Journal of Quantum Electronics, 1988, 24(8): 1 698-1 710.

[3]Bass F G, Fucks I M.Wave scatteing from statistically rough surfaces [M].London: Pegamon, 1979.

[4]A K Fung.A semi-empirical sea-spectrum model for scattering coefficient estimation [J].IEEE J .of Oceanic Engineering ,1982, OE27 (4) : 166-176.

[5]Eric I Thorsos.The validity of the perturbation approximation for rough surface scattering using a Gaussian roughness spectrum.[J].Acoust.Soc.Am.1989, 7, 86(1): 261-277.

[6]J M Soto-Crespo, M Nieto-Vesperinas a, A T Friberg.Scattering from slightly rough random surfaces: a detailed study on the validity of the small perturbation method [J].Opt.Soc.Am.A.1990, 7, 7(7): 1 185-1 201.

[7]Didascalou D, Dttling M, Geng N, et al.An Approach to Include Stochastic Rough Surface Scattering Into Deterministic Ray-Optical Wave Propagation Modeling [J].IEEE Transactions On Atennas And Propacation, 2003, 51(7): 1 508-1 515.

[8]Ren X C, Guo L X.Study on Optical Wave Scattering from Slightly Gaussian Rough Surface of layered medium [J].Chinese Opics Letters, 2007, 5(10): 605-608.

[9]ABOSEIDA O M, BISHA Y S T, MOHAMED ELMORABIE K.Farfield radiated from vertical magnetic dipole in the sea with a rough upper surface [J].IEEE Trans.Geosci.Remote Sensing.2006, 44(8): 2 135-2 142.

[10]任新成, 郭立新.基于改进二维分形海面模型的分层海面电磁散射分析 [J].上海航天, 2009, 4: 1-6.

[11]王蕊, 郭立新, 秦三团, 等.粗糙海面及其上方导体目标复合电磁散射的混合算法研究 [J].物理学报, 2008, 57(6): 3 473-3 480.

[12]陈晓翔, 戴泳斯, 吴波, 等.SeaWinds散射计海面风场的几何反演算法 [J].遥感学报, 2009, 13(4): 585-590.

[13]黄泽贵, 童创明, 胡国平, 等.粗糙海面后向增强效应研究 [J].微波学报, 2007, 23(2): 14-18.

[14]张德海, 张俊荣, 王丽巍.海洋微波遥感中的介电常数 [J].遥感技术与应用, 1994, 9(3): 43-52.

Study on Electromagnetic scattering from the rough sea surface with A.K.Fung spectrum using the small perturbation method

TIAN Wei, REN Xin-cheng, Huang Bao-rui

(School of Physics and Electronic Information, Ya nan University, Yan’an 716000, China)

TN011

A

1001-6932(2011)02-0227-08

2010-04-13；收修改稿日期：2010-10-15

中国博士后科学基金（20090461284）。

田炜（1978-），男，陕西绥德人，讲师，硕士，主要研究方向为复杂系统和随机介质中电磁（光）波的传播、散射及应用。电子邮箱：ydfsyy@163.com。