复杂单摆的KAM理论

梁建莉,汤龙坤

(华侨大学数学科学学院,福建泉州 362021)

复杂单摆的KAM理论

梁建莉,汤龙坤

(华侨大学数学科学学院,福建泉州 362021)

建立了一类复杂单摆的运动方程.首先利用一个动量守恒的首次积分将二自由度系统转化为单自由度系统,然后利用 KAM理论,将重力能量作为小扰动项,研究了复杂单摆的运动规律.研究表明:当重力能量与总能量相比很小时,或者单摆总能量充分大时,复杂单摆的KAM不变曲线仍然存在,整个系统做拟周期运动,扰动系统仍然具有无重力系统的运动规律.

复杂单摆;无重力系统;KAM理论;哈密顿系统

哈密顿动力系统的中心问题是动力学稳定性.KAM理论是哈密顿系统研究理论发展的里程碑,它对物理学、天文学、力学等有关领域产生了深远的影响.半个世纪以来,数学力学家在使用和研究KAM理论方面做了大量的工作,如直接否定了哈密顿系统遍历性的猜测,解决了长期悬而未决的特罗央小行星群运动稳定性问题.文献[1-2]采用 KAM理论研究了复杂双摆和陀螺仪的运动稳定性,文献[3-4]采用 KAM理论研究了太阳系的稳定性、木星附近卫星的运动等.本文利用 KAM理论研究一类复杂单摆的运动性质和稳定性问题.

1 运动方程

复杂单摆的运动系统模型,如图1所示.图1中:重物M1的质量为m1,可沿光滑水平面移动;摆锤M2的质量为m2,两个物体用无重杆AB连接,杆长为l.重物和单摆组成的系统具有两个自由度.选取重物的水平位移 x和杆AB偏离铅直线的角度φ为广义坐标.设重物和单摆为两个质点,则系统动能为式中:(x,φ)为广义坐标为广义速度.系统势能即重力势能为由此可得系统的Lagrange函数为

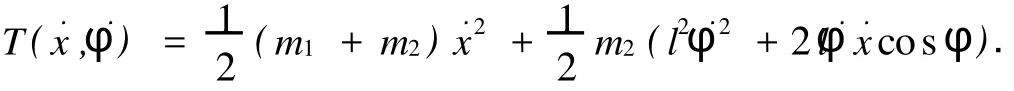
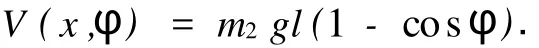
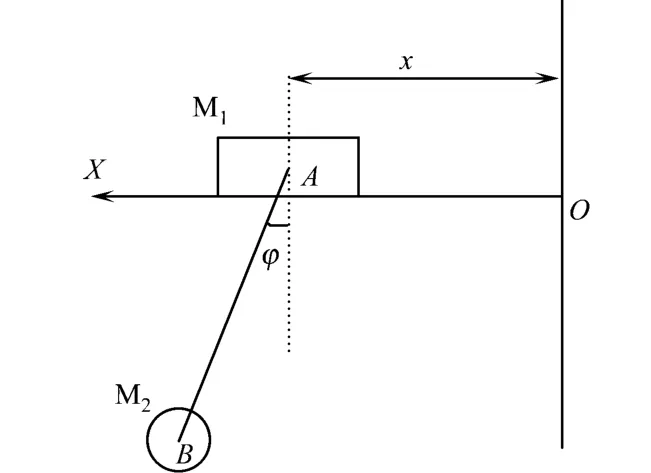
图1 复杂单摆模型Fig.1 Model of the comp lex pendulum

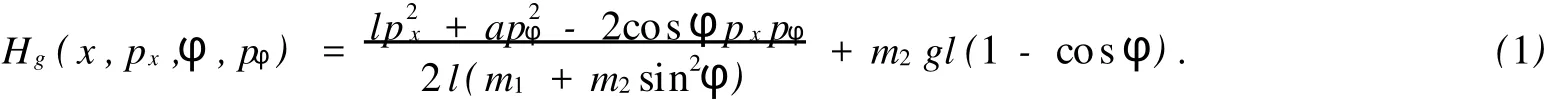
由此,可得复杂单摆系统的哈密顿方程为

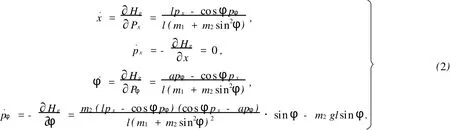
2 无重力系统的运动

复杂单摆系统是一个不可积的哈密顿系统.首先,研究无重力时的运动情形,即g=0的情形.这时系统是可积的,对应的哈密顿函数为

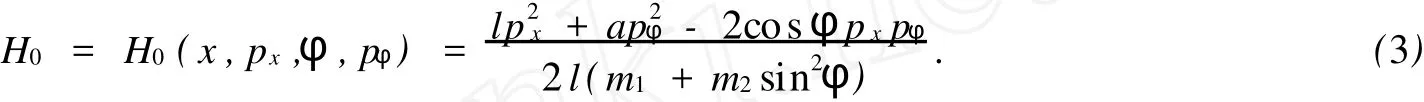
由能量守恒可得,系统的一个首次积分为

由式(2)可知,px为常数,即重物的动量守恒.对任意给定的H0=h,由式(3)可得局部解为

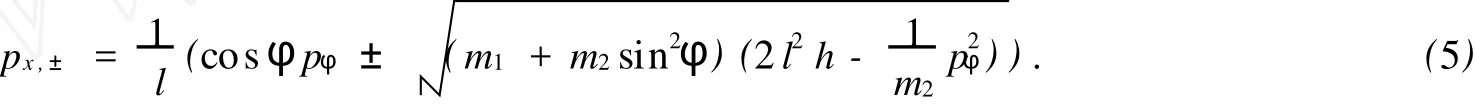
将式(5)代入式(2),消去px可得

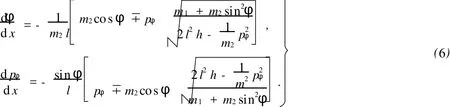
记px,±=Λ0,±(φ,pφ),则有

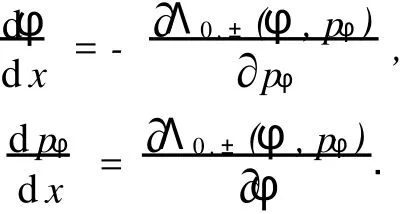
即系统(6)是以Λ0,±(φ,pφ)为哈密顿函数的哈密顿系统,此系统的一个首次积分为

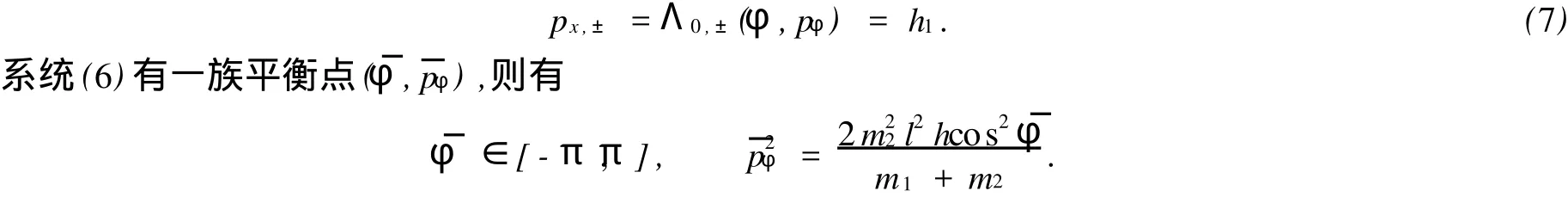
这些平衡点都是不稳定的平衡点,并且构成相平面上的两条连续曲线.

系统(6)的平衡点对应的两个特殊值为

到20周，宝宝体重增加到300克，从16周的120克到20周的300克，这4周时间里宝宝增重180克，平均每周才45克。孕妇到20周应该可以增重4千克。如果孕妈妈想要控制体重，这时增重3千克即可，因为在20周前增重的4千克里有2千克是非必需增重的间质，相对而言可以减少一点，所以增重3千克也可以。

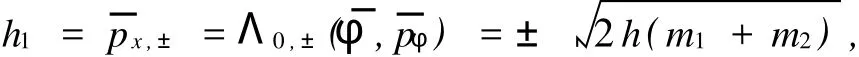
这样就对应两族点,构成两条连续曲线为

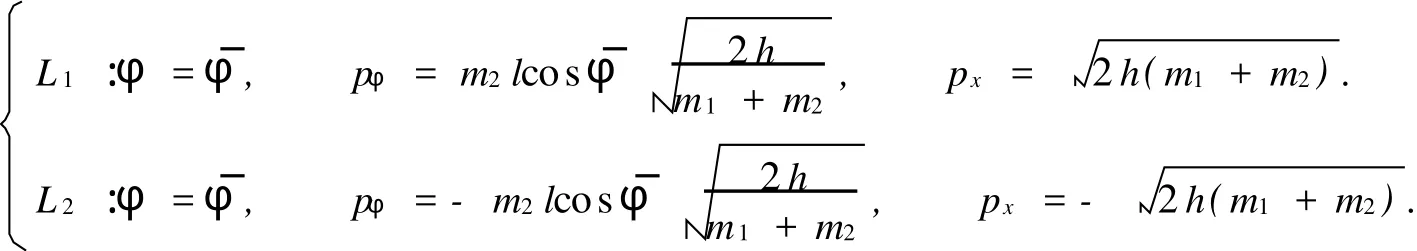
当参数h和h1固定时,对任意x,式(4),(7)定义了两个二维流形.把式(4)定义的二维流形记作M0(x),称为等能量面,M0(x)同胚于一个二维环面T2;把式(7)定义的二维流行记作当h和h1给定后,一个具体的运动对应于上述两个二维流形的交线,它通常是一条或两条闭曲线,把它们称为h1-曲线.通过分析,可以得到如下4点结论.

(1)当h1=时,环面M0(x)上h1-曲线为曲线L1或L2,它是环面M0(x)上的一条闭曲线.

(2)当h1=0时,由式(4)可得

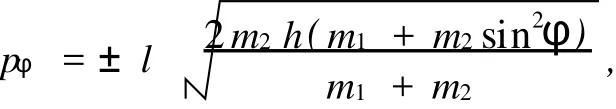
环面M0(x)上h1-曲线是两条互不相交的闭曲线,它们分别是环面M0(x)的外赤道和内赤道.

(3)当 -时,环面M0(x)上的h1-曲线是两条互不相交的闭曲线.一条几乎位于M0(x)的外半部,同伦于M0(x)的外赤道;而另一条几乎位于M0(x)的内半部,同伦于M0(x)的内赤道.

(4)当>2h(m1+m2)时,环面M0(x)和流形M h1不相交,解不存在.

系统的作用变量I(h1)可由以下过程求出.即

即该系统满足柯尔莫哥洛夫非退化条件.

3 KAM理论

对系统(2),哈密顿函数可以写为

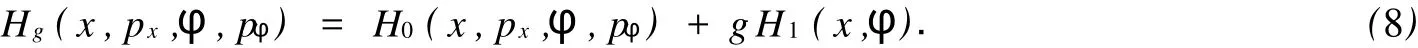
其中:H1(x,φ)=m2l(1-cosφ),对应于φ以2π为周期.对于任意Hg=hg∈R+,式(8)等价于

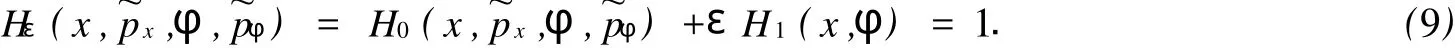
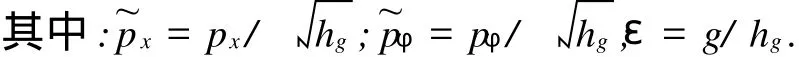
当能量hg很大时,εH1(x,φ)很小,这样复杂单摆系统就可以看作是无重力运动的周期扰动.如果存在

对于固定的h∈R+和x,则式(10)定义了一个等能量面Mε(x).对于充分小的ε>0,它同胚于二维环面T2.由式(10)可局部解得

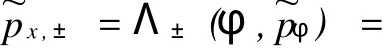
已证明无重力系统即未扰系统的每个解关于φ都是周期解,始终在不变环面上,解的周期取决于相轨线的位置.由于Λ0,±(φ,pφ)满足柯尔莫哥洛夫非退化条件,由 KAM理论可得如下结论.

定理1 对扰动系统(9),当ε>0充分小时,扰动系统的轨线仍保持在不变环面上.

4 结论

从相平面上看,对于未扰系统的平衡曲线,扰动系统也有相应的固定曲线,它们对应于关于φ的周期解.在固定曲线周围的大部分不变曲线仍然存在情况下,与未扰系统的不变曲线相比,其仅仅发生了微小形变,但破裂的曲线也构成稠密集.

同样,当ε>0充分小时,扰动系统也存在与未扰系统的不变环面相对应的不变环面,其上的流是拟周期流,并且此不变环面充分接近未扰系统的不变环面.扰动系统的不变曲线存在表明,扰动系统仍然具有无重力系统的运动规律.

[1]胡志兴,管克英.复杂双摆的 KAM定理[J].高校应用数学学报:A辑,1999,14(2):147-154.

[2]胡志兴,管克英.陀螺仪运动的混沌与 KAM理论[J].应用数学学报,2000,23(2):212-220.

[3]ARNOLD V I.Mathematical methods of classical mechanics[M].New York:Sp ringer-Verlag,1978.

[4]程崇庆,孙义燧.哈密顿系统中的有序和无序运动[M].上海:上海科技出版社,1996.

(责任编辑:陈志贤英文审校:张金顺,黄心中)

KAM Theory of the Complex Pendulum

LIANG Jian-li,TANG Long-kun
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

The motions of a comp lex pendulum is studied in this paper.A two degrees systems is transformed into a single degree system by means of a momentum conservation.The system is studied by treating the gravitation as a small perturbation in KAM theory.It is show n that w hen the gravitational energy is small compared with the total energy,o r the total energy is sufficiently large,there still exists the KAM invariant curves.It is also show n that the system is a quasi periodic system and the motions of the gravity-free system can be kept to the perturbation system.

comp lex pendulum;gravity-free system;KAM theory;Hamiltonian system

O 317;O 175.13

A

1000-5013(2011)02-0231-04

2009-04-11

梁建莉(1979-),女,讲师,主要从事哈密顿动力系统的研究.E-mail:liangjl@hqu.edu.cn.

国务院侨办科研基金资助项目(08QZR10)