Beurling-Ahlfors扩张伸张函数在非光滑摄动下的稳定性
林峰
(华侨大学数学科学学院,福建泉州 362021)
Beurling-Ahlfors扩张伸张函数在非光滑摄动下的稳定性
林峰
(华侨大学数学科学学院,福建泉州 362021)
给出一种非光滑摄动的定义,讨论M-拟对称函数h(x)发生非光滑摄动时,伸张函数D(z)的稳定性问题.证明在边界值发生这种摄动时,边界值的M-拟对称性保持不变,其Beurling-Ahlfo rs扩张的伸张函数也具有稳定性,同时得到该伸张函数的误差估计式.
Beurling-Ahlfors扩张;伸张函数;非光滑摄动;稳定性
设h(x)是实轴上的连续递增函数,h(∞)=∞,如果满足所谓的M-条件,即
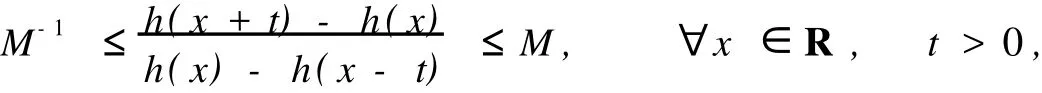
则称h(x)是M-拟对称函数.复函数φ(z)=u(x,y)+iv(x,y),有
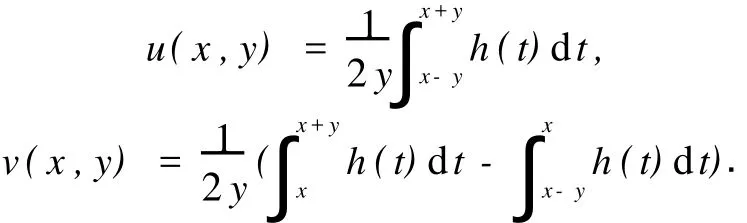
称φ(z)为h(x)的Beurling-Ahlfo rs扩张,函数h(x)称为φ(z)的边界函数或边界值,记
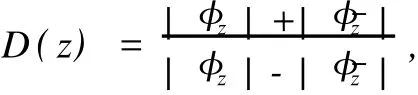
则D(z)称为 φ(z)的伸张函数[1-2].
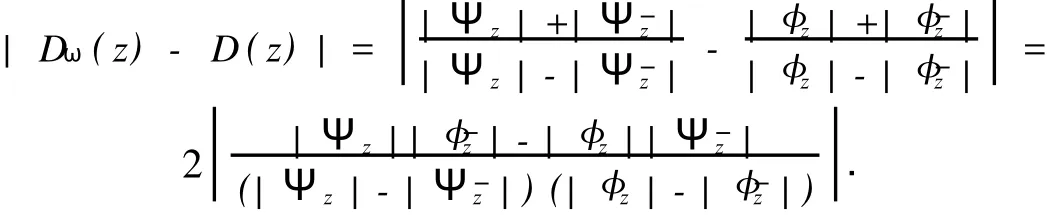
在假设M-拟对称函数h(x)满足某种条件下,文献[2]讨论了Beurling-Ahlfors扩张及其伸张函数的某些性质.对于任意x∈R,存在εx>0,当0 式(1)中:K+和K-是与x无关的常数.在假设M-拟对称函数h(x)满足上述条件下,文献[3]讨论了当边界值h(x)发生光滑摄动时,伸张函数D(z)的稳定性问题.本文讨论h(x)发生非光滑摄动时,伸张函数D (z)的稳定性问题.以下均假设M-拟对称函数h(x)满足上述条件(1),并记K=min(K+,K-). 以Ω(R)表示R上满足Lipschitz条件的有界连续函数类.对任意ω∈Ω(R),存在只与ω有关的非负数δ,使得对于任意x,y∈R,有 显然,Ω(R)是线性空间.在其上定义范数为 其中: 设ρ0>0,记B(ρ0)={ω∈Ω(R)|‖ω‖1<ρ0}.对于ω∈B(ρ0),称hω(x)=h(x)+ω(x)为h(x)的非光滑摄动.以Ψ(z)表示hω(x)的Beurling-Ahlfors扩张,Dω(z)表示Ψ(z)的伸张函数,如果 在上半平面一致成立,则称伸张函数D(z)关于边界值的非光滑摄动是稳定的[4-5]. 引理1[3]对于任意x∈R及任意t>0,有 引理2 设ω∈Ω(R),则对于任意a,b∈R,有 证明 对任意η>0,由定义可得 由η的任意性,可得 证毕. 证明 对于任意x1,x2∈R,x1 由此可知,hω(x)为连续递增函数,h(∞)=∞. 仿照上述证明,可得 证毕. 由此容易估计出|U x|≤‖ω‖1,|U y|≤‖ω‖1,|V x|≤‖ω‖1,|V y|≤‖ω‖1. 事实上,选其中的一个给出估计过程为 于是,利用引理2有 由式(2)有 同理,由式(3)可得 证毕. 定理1 当ρ0 在上半平面一致成立,即D(z)是稳定的.其误差估计式为 证明 经化简可得 利用引理4,可得 于是,可得 利用引理3,5,可得 且有 在上半平面一致成立.证毕. [1]郑学良.Beurling-Ahlfo rs扩张的伸张函数与ID-同胚[J].数学学报,2002,45(5):1036-1040. [2]林峰.Beurling-Ahlfo rs扩张的伸张函数的边界极限性质[J].华侨大学学报:自然科学版,2004,25(4):352-355. [3]林峰.Beurling-Ahlfo rs扩张的伸张函数关于边界值的稳定性[J].南昌大学学报:理科版,2005,29(5):432-434. [4]王小林,龚亚方.一类奇异积分和Cauchy积分关于积分曲线的稳定性[J].数学学报,1999,42(2):343-350. [5]ZHANG Hong-mei,WANGChuan-rong,ZHU Yu-can.Stability of solutions to Hilbert boundary value problem under perturbation of the boundary curve[J].JMath Anal App l,2003(284):601-617. [6]LEHTINEN M.The dilatation of Beurling-Ahlfors extension quasisymmetric function[J].Ann Avad Sci Fenn Ser A IMath,1983,8(1):187-191. (责任编辑:陈志贤英文审校:张金顺,黄心中) Stability of Dilatation Function of Beurling-Ahlfors Extension Under Non-Smooth Perturbation L IN Feng In this paper,a definition of non-smooth perturbation is given.The stability of dilatation function of its Beurling-Ahlfors extension is diecussed under the invariant ofM-quasisymmetric function.The corresponding error estimate is obtained. Beurling-Ahlfors extension;dilatation function;non-smooth perturbation;stability O 174.5 A 1000-5013(2011)02-0222-04 2009-06-24 林峰(1962-),男,副教授,主要从事函数论的研究.E-mail:lfeng@hqu.edu.cn. 福建省自然科学基金资助项目(2007J0183)
1 问题的提出
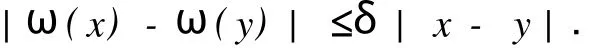
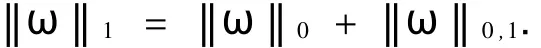
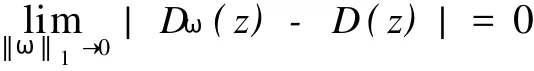
2 预备知识

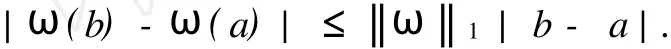
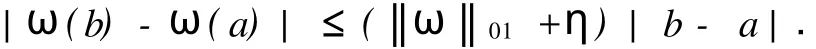
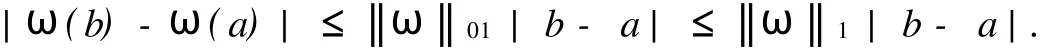
3 主要结果

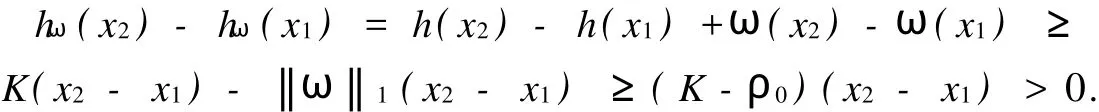
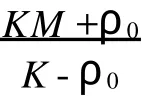
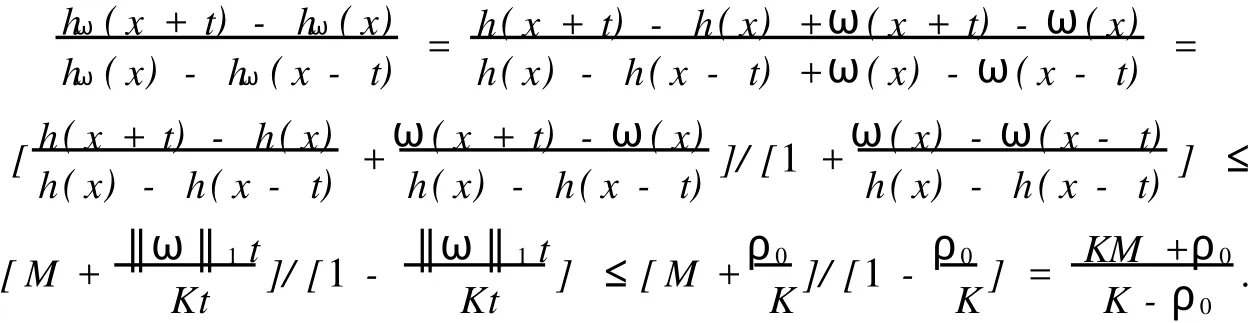
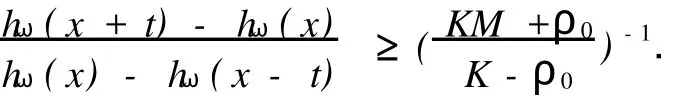
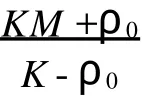
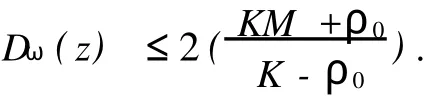

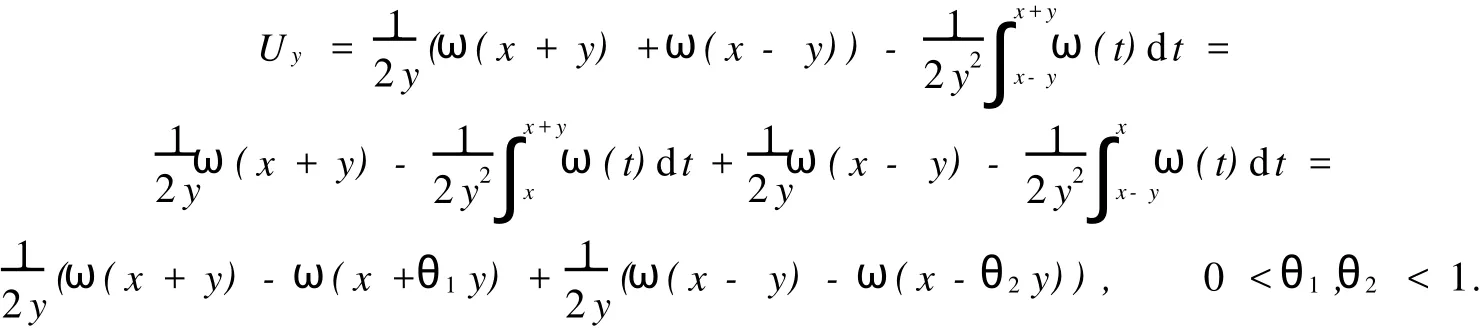
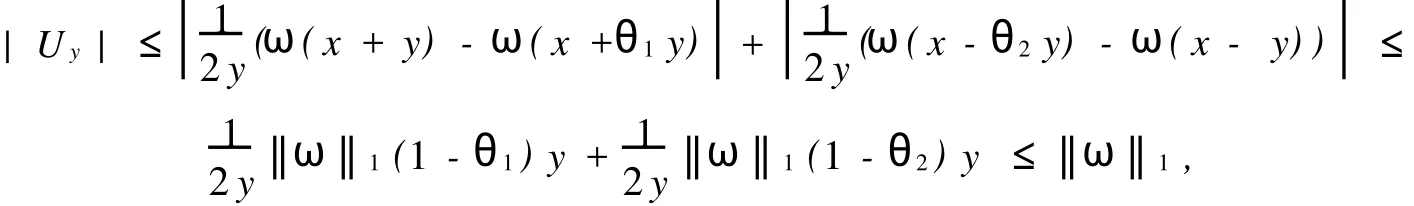
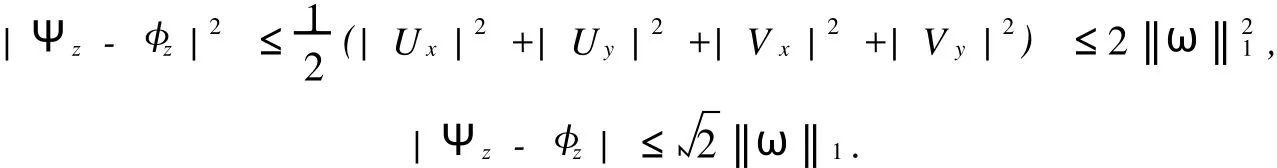
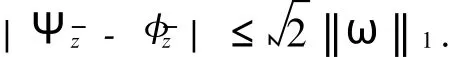
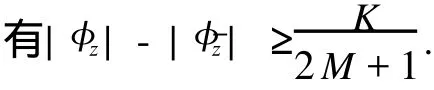

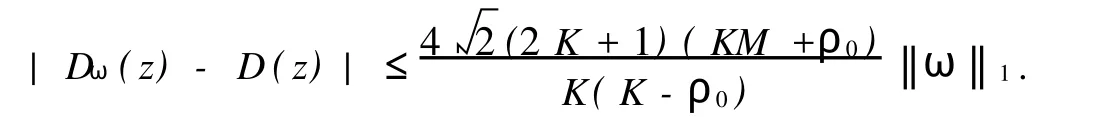
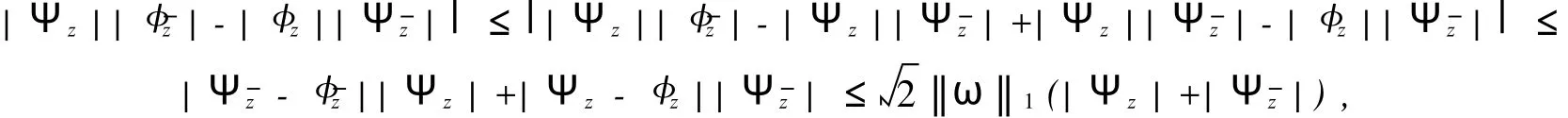


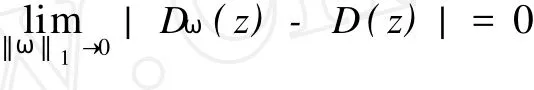
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

