复宗量厄米双曲余弦高斯光束在湍流大气中的传输特性

(华侨大学信息科学与工程学院,福建泉州 362021)

刘永欣,蒲继雄,陈子阳,王涛

复宗量厄米双曲余弦高斯光束在湍流大气中的传输特性

(华侨大学信息科学与工程学院,福建泉州 362021)

刘永欣,蒲继雄,陈子阳,王涛

根据广义的惠更斯-菲涅耳原理,推导了复宗量厄米双曲余弦高斯(EHChG)光束在湍流大气中传输时光强分布的理论公式,并研究光束在湍流大气中的传输变化规律.研究发现,EHChG光束在湍流大气中传输时,光强分布均趋于高斯分布.在湍流大气的影响下,EHChG光束由完全相干光变成部分相干光,并且随着传输距离和湍流强度的增加,光束的空间相干性变差.研究还发现,光束的桶中功率与湍流大气的强度、传输距离及光束参数m,n有关.

EHChG光束;湍流大气;空间相干度;桶中功率

对于复宗量厄米高斯(EHG)光束和双曲余弦高斯(ChG)光束的研究已经比较深入[1-2],一类包含上述两种光束的,更加普遍的新型光束——复宗量厄米双曲余弦高斯(EHChG)光束正日益受到关注.复宗量厄米双曲余弦高斯光束是厄米正弦类高斯光束和厄米双曲余弦高斯光束的特殊形式[3].文献[3 -4]研究了EHChG光束在自由空间的传输特性,推导出在近轴条件下有光阑和无光阑光学系统的传输方程,并得到了可进行直观物理分析的解析结果.激光束在大气湍流中的传输是一个既有重要理论意义又有实际应用意义的课题,人们相继研究了各种激光束在大气湍流中的传输特性和空间相干性的变化[5-7],但有关EHChG光束在湍流大气中的传输研究仍未见报道.本文推导了EHChG光束在湍流大气中传输时光强分布的理论公式,研究EHChG光束在湍流大气中的传输变化规律.

1 理论分析

假设在z=0平面复宗量厄米双曲余弦高斯(EHChG)光束的场分布表示为

式中:w0为束腰宽度;Hn(·)为n阶厄米多项式;Ω0=m/w0,m为偏轴参数.当n=0时,光强分布为ChG光束;当m=0时,光强分布为EHG光束.随着m,n的增加,光强分布越偏离轴心,如图1所示.

根据广义惠更斯-菲涅耳原理,复宗量厄米双曲余弦高斯光束通过大气湍流传输z距离后,其交叉谱密度函数可表示为[8]

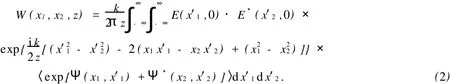
式(2)中:波数k=2π/λ;Ψ(x′,x)表示大气湍流对球面波影响的随机相位因子;〈·〉表示系综平均.采用Rytov相位结构函数的二次近似,可以得到

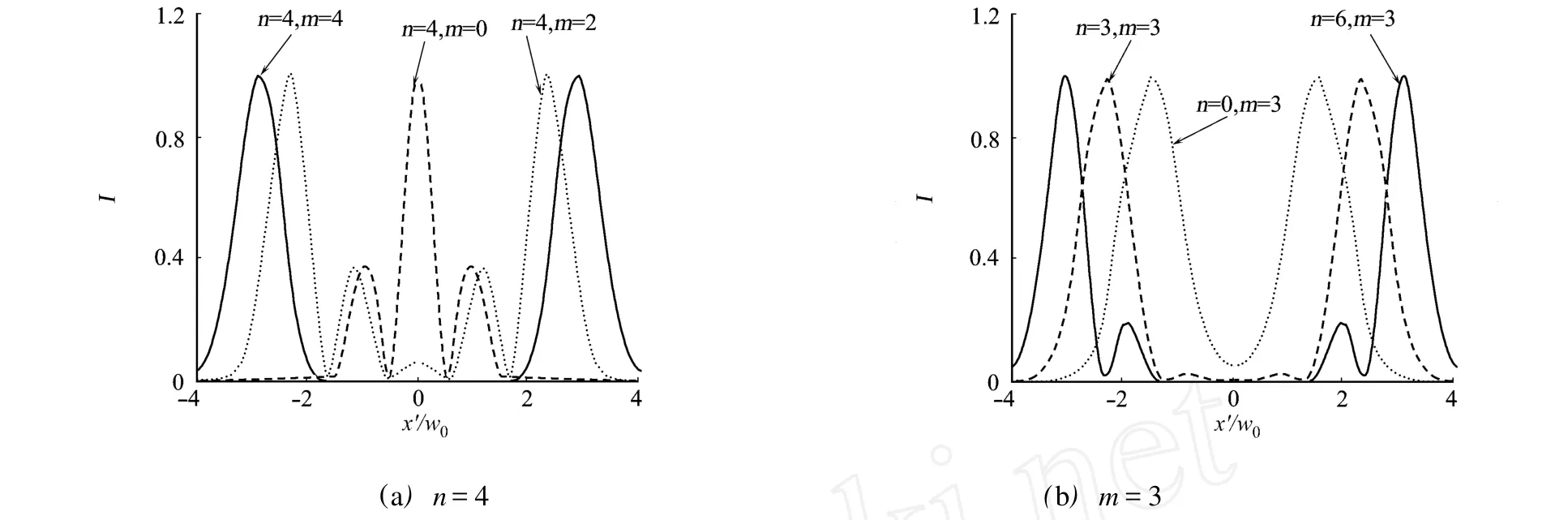
图1 EHChG光束在z=0平面的归一化光强分布图Fig.1 Normalized intensity of EHChG beams at the z=0 plane

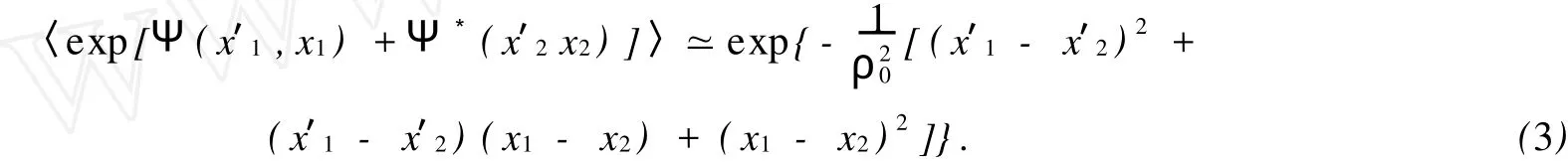
式(3)中:ρ0为球面波通过大气湍流的相干长度,ρ0=()-3/5为折射率结构常数,表征湍流的强弱.

将式(1)代入式(2),利用积分式

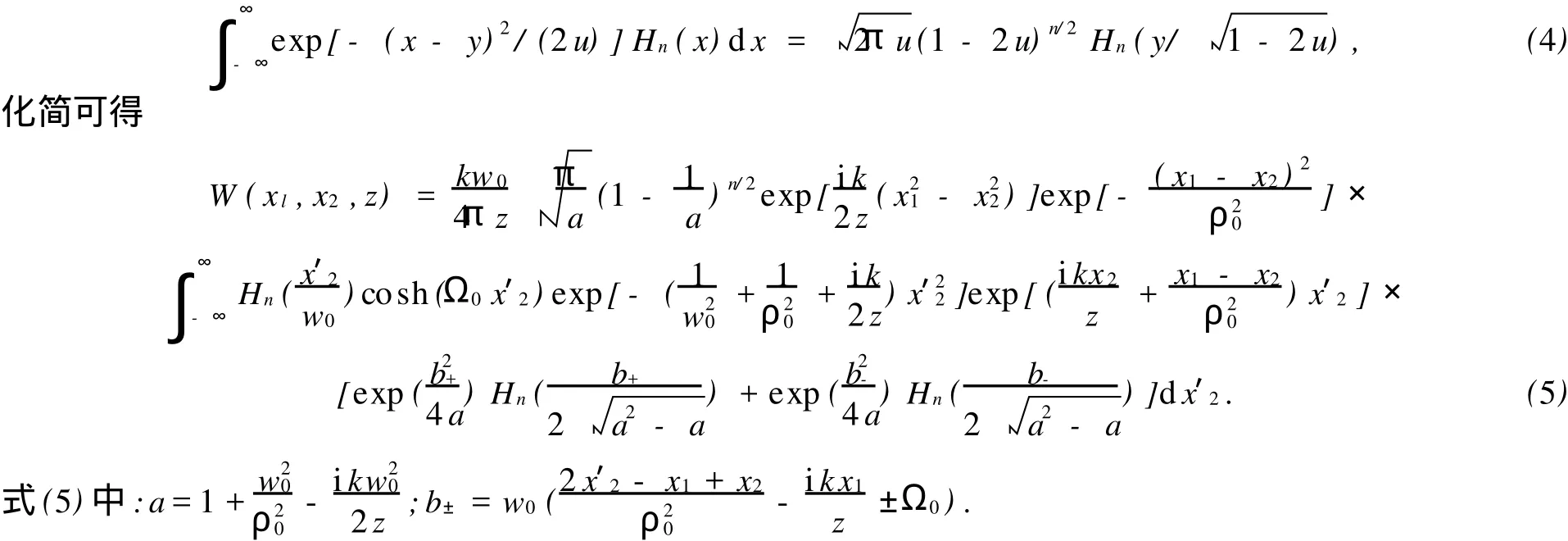
令式(5)中x1=x2=x,得到EHChG光束在大气湍流中传输的光强为

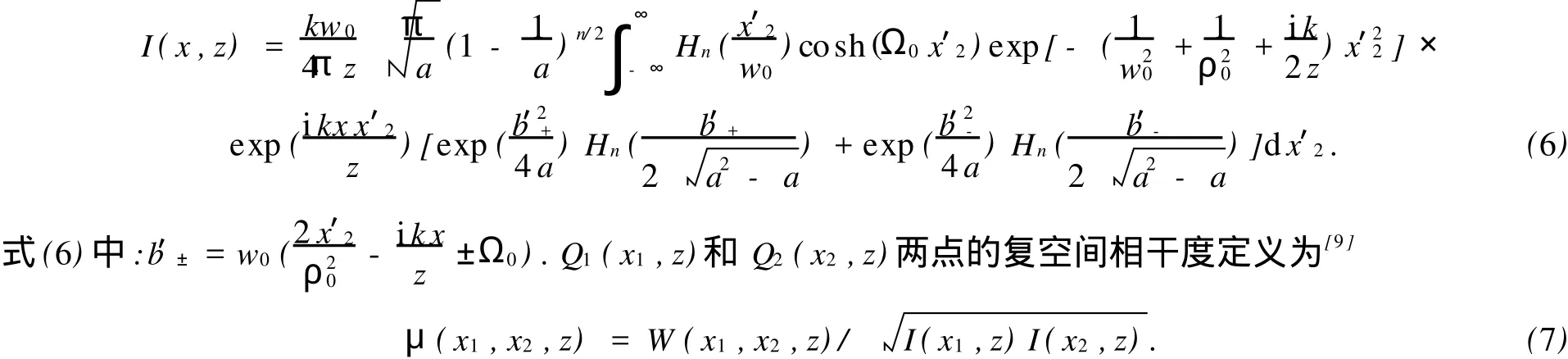
为简单起见,只考虑轴外点Q1(x,z)和轴上点Q2(x,z)的复空间相干度.于是,有

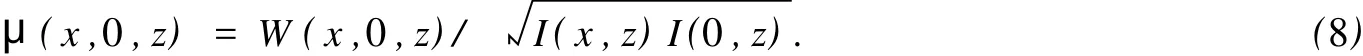
为评价EHChG光束在湍流大气中传输后的光束质量,可引入桶中功率(Power in Bucket,PIB).桶中功率(PB)定义:在远场z平面上,某一给定的桶尺寸内所围住功率占总功率的百分比[10]

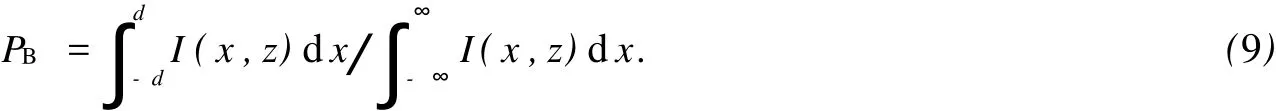
式(9)中:d为桶的半宽度;I(x,z)为光束在远场的光强分布.0≤PB≤1,PB值越大,则光束质量越高.式(9)表明,桶中功率与光束的光强分布、桶尺寸大小的选取有关系.

2 计算模拟与分析

利用式(5),(6),(8)和式(9),对EHChG光束通过大气湍流传输的光强分布、空间相干度和桶中功率作数值计算模拟,分析了其随各参数的变化情况,结果如图2～4所示.数值计算中,参数w0=0.02 m,λ=800 nm.

通过湍流大气和自由空间传输后,EHChG光束(n=4,m=2)在不同z平面的归一化光强分布,如图2所示.从图2(a),(b)可看出,EHChG光束在湍流大气中传输足够长的距离后,光强分布均趋于高斯分布,而湍流强度越强,所需的传输距离越小.从图2(c)可看出,EHChG光束在自由空间中传输时,随着传输距离的增大,光束逐渐展宽,但光强分布并不会趋于高斯分布,而是基本形状保持不变.

图2 传输后EHChG光束在不同z平面的归一化光强分布Fig.2 Normalized intensity of a EHChG beam propagating at different z planes

在湍流大气传输后,EHChG光束(n=4,m=2)的复空间相干度的绝对值|μ(x,0,z)|随x/w0的变化,如图3所示.从图3(a)可看出,在自由空间传输时,EHChG光束的空间相干度均为1,依然保持完全相干光不变;在湍流大气中传输时,EHChG光束受湍流强度的影响,变成部分相干光,并且在传输相同距离后,湍流强度越大,光束的空间相干性变差.

从图3(b)可以看出,由于湍流的存在,随着传输距离的增加,光束的空间相干性变差.由于湍流引起光束的波前起伏,会使复空间相干度的实部在横向分布出现震荡现象,从而使得图3中复空间相干度的绝对值在横向分布产生波动.

通过不同强度湍流大气传输后,EHChG光束在不同z平面的桶中功率(PB)随d/w0的变化,如图4所示.比较图3(a),(b)可知,在相同强度湍流大气情况下,EHChG光束传输距离越远,对于给定尺寸d,光束的PB越小.在同一z平面上,湍流强度越大,对于给定尺寸d,光束的PB越小.但随着湍流强度的减弱,对光束的PB影响也变小,逐渐趋于自由空间传输的情况.

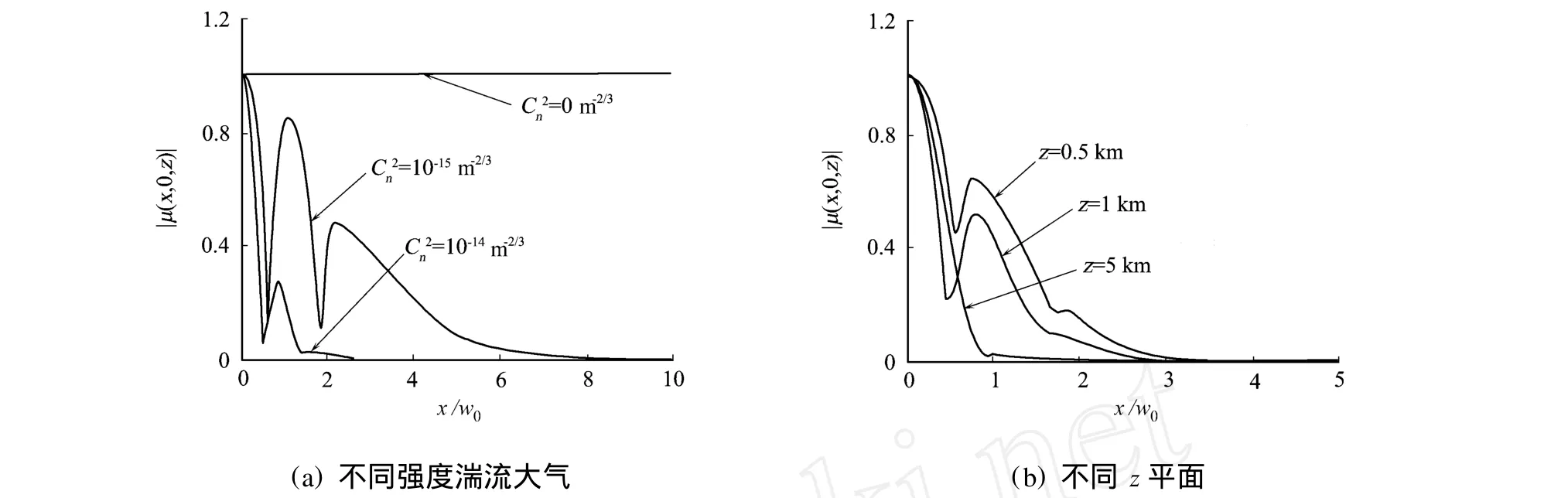
图3 EHChG光束复空间相干度绝对值随x/w0的变化Fig.3 Absolute value of the comp lex spatial coherence of the EHChG beam vs x/w0 at different z planes

比较图4(a)～(d)可知,在同一z平面上,对于相同的湍流强度和桶尺寸,n=2,m=1的 EHChG光束在湍流中的可聚焦能力好.这是因为随着m和n增加,光强分布越来越偏离轴心的缘故.

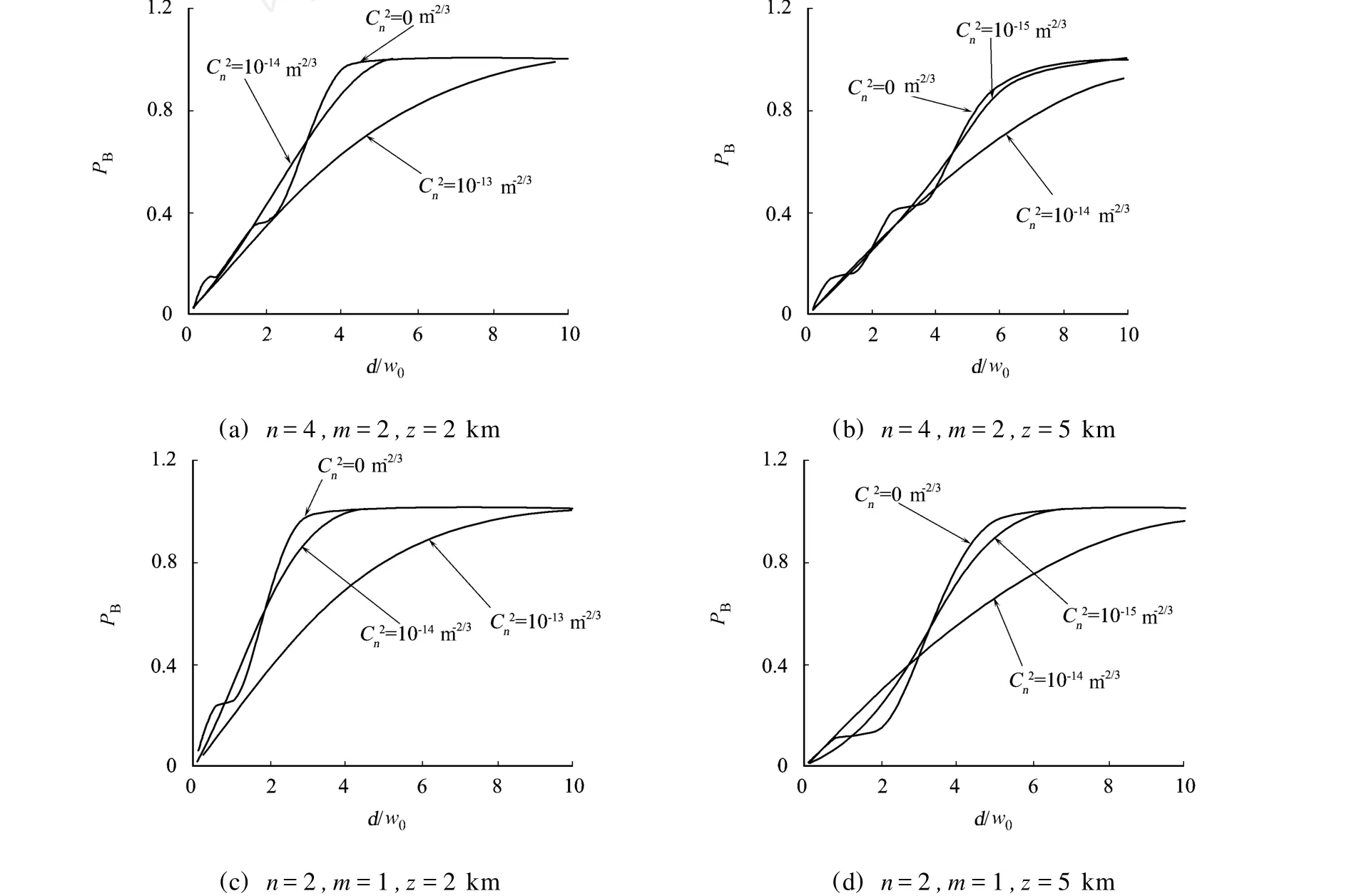
图4 EHChG光束在不同z平面的桶中功率随d/w0的变化Fig.4 Power in bucket of a EHChG beam vs d/w0 at different z planes

3 结论

推导了复宗量厄米双曲余弦高斯(EHChG)光束在湍流大气中传输时光强分布的理论公式,研究光束在湍流大气中的传输变化规律,得到以下5点结论.

(1)EHChG光束在湍流大气中传输足够长的距离后,光强分布均趋于高斯分布.

(2)EHChG光束受湍流强度的影响,变成部分相干光,并且随着传输距离的增加及湍流强度的增大,光束的空间相干性变差.

(3)EHChG光束在湍流大气中传输时,桶中功率(PB)与湍流大气的强度、传输距离及光束参数m,n有关.

(4)对于给定尺寸d,湍流强度越大,传输距离越远,光束的桶中功率越小;随着湍流强度的减弱,对光束的桶中功率影响也变小,逐渐趋于自由空间传输的情况.

(5)随着光束参数m和n增加,光强分布越来越偏离轴心,EHChG光束在湍流中的可聚焦能力也随之变差.

为简便起见,只分析了一维情况,由于x,y方向是分离的,所以二维情况也容易得到.研究EHChG光束在湍流介质中的传输,具有一定的应用价值和意义.

[1]LUO Shi-rong,LÜBai-da.Propagation of the kurtosis parameter of elegant Hermite-Gaussian and Laguerre-Gaussian beams passing through ABCD system s[J].Optik,2002,113(5):227-231.

[2]CHU X,N IY,ZHOU G.Propagation of cosh-Gaussian beams diffracted by a circular aperture in turbulent atmosphere[J].ApplPhy(B),2007,87(3):547-552.

[3]YU Song,GUO Hong,FU Xi-quan,et al.Propagation properties of elegant Hermite-cosh-Gaussianlaser beams [J].Opt Commun,2002,204(1/6):59-66.

[4]DENG Dong-mei.Propagation of elegant hermite cosine gaussian laser beams[J].Opt Commun,2006,259(2):409 -414.

[5]EYYUBOGLU H T,BA YKAL Y,SERMU TLU E.Convergence of general beams into Gaussian-intensity profiles after propagation in turbulent atmosphere[J].Opt Commun,2006,265(2):399-405.

[6]WANG Tao,PU Ji-xiong,CHEN Zi-yang.Propagation of partially coherent vortex beams in a turbulent atmosphere[J].Op t Eng,2008,47(3):036002.

[7]JIX,JIG.Spatial correlation propertiesof apertured partially coherent beam s propagating through atmospheric turbulence[J].App l Phys(B),2008,92(1):111-118.

[8]ANDREWS L C,PH ILL IPS R L.Laser beam propagation through random media[M].Bellingham:SPIE press, 1998.

[9]MANDEL L,WOLF E.Optical coherence and quantum op tics[M].Cambridge:Cambridge University Press,1995.

[10]SIEGMAN A E,NEM ES G,SERNA J,et al.How to(maybe)measure laser beam quality[J].OSA Trends in Optics and Photonics Series,1998,17(5):184-199.

(责任编辑:钱筠英文审校:吴逢铁)

Propagation Properties of Elegant Hermite-Coch-Gaussian Beams in a Turbulent Atmosphere

LIU Yong-xin,PU Ji-xiong, CHEN Zi-yang,WANG Tao
(College of Information Science and Engineering,Huaqiao University,Quanzhou 362021,China)

Based on the extended Huygens-Fresnel principle,the theoretical formula of the optical intensity distribution for an Elegant Hermite-cosh-Gaussian(EHChG)beams which propagate in a turbulent atmosphere has been derived, and then the propagation properties of such beam in the turbulent atmosphere have been investigated in detail.It is found that the intensity distribution of EHChG beams will approach to a Gaussian profile after propagating in the turbulent atmosphere.It is also found that a coherent EHChG beam will change into a partially coherent one at the influence of the turbulent atmosphere,and the coherence of beam s is getting worse for a longer propagation distance o r a stronger atmospheric turbulence.In addition,the power in bucket(PIB)of the EHChG beam s has been discussed.It is shown that the PIB of the EHChG beam propagating in turbulent atmosphere is related with the the intensity of the atmospheric turbulence,the propagation distance,and the beam parametermandn.

EHChG beams;turbulent atmosphere;spatial coherence′s degree;power in bucket

O 435

A

1000-5013(2011)02-0145-05

2009-04-23

刘永欣(1979-),女,讲师,主要从事激光光束传输变换的研究.E-mail:yongxin@hqu.edu.cn.

福建省科技计划重点项目(2007H0027);福建省自然科学基金资助项目(A 0810012);华侨大学科研基金资助项目(07HZR29)