无索引空间数据库的基于最优点的集合最近邻查找算法
骆炎民,陈维斌,廖明宏
(1.华侨大学计算机科学与技术学院,福建泉州 362021; 2.厦门大学信息科学与技术学院,福建厦门 361005; 3.厦门大学软件学院,福建厦门 361005)
无索引空间数据库的基于最优点的集合最近邻查找算法
骆炎民1,2,陈维斌1,廖明宏3
(1.华侨大学计算机科学与技术学院,福建泉州 362021; 2.厦门大学信息科学与技术学院,福建厦门 361005; 3.厦门大学软件学院,福建厦门 361005)
针对度量空间中的无索引空间数据库,提出一种基于最优点的集合最近邻查找算法及其改进算法.采用真实数据集与人工生成的数据集对算法进行测试,评估所提出算法的效率.实验结果表明,所提算法的效率优于组最近邻居查询算法,并且对于高维数据空间,所提出的算法有较高的稳定性.由于查询区域中数据点的数量比较少,改进的基于最优点的集合最近邻查找算法的效率总体上要比改进前高.
空间数据库;最近邻;集合最近邻;查询区域
集合最近邻(Aggregate Nearest Neighbor,ANN)是由最近邻(Nearest Neighbor,NN)演变而来的.它在许多研究领域中得到广泛的应用,如地理信息系统[1-2]、数据挖掘中的分类[3]和异常点检测[4]等.空间数据一般具有高维、海量等特性,如何高效地在空间数据库中进行各种最近邻查询,已经成为空间数据库及数据挖掘中的一个重要研究内容.目前,大多数的NN和ANN算法的主要思想是基于空间索引结构的,通过对空间数据库中的数据进行裁剪,以提高查询效率.在众多的索引结构中,R-树[5-7]是最流行的一种.这些算法大部分在低维数据空间都能获得理想的执行结果和效率,而有研究表明,传统的索引方法在高维数据空间中将失去效果.文献[8]指出,在高维数据空间中,由于存在所谓的“维灾”的问题,传统的NN和ANN查询可能会失去意义.在空间数据库的最近邻查找中,查找效率是一个关键问题.因此,为了缩小查询空间范围,以减少查询所需要的时间,人们引进了各种各样的空间索引机制.在空间数据库中,数据集一般通过高维空间索引(Spatial Access M ethods,SAM)方法建立相关索引结构,如R-树[9],R*-树[10]等.因此,大部分的最近邻查询算法都利用这些索引机制来实现高维数据空间中的最近邻及k最近邻查询[11-13].此外,一些基于距离空间的索引结构,如 MB+-树[14], GNA T[15]和MVP-树[16]等也用于相似性查询.本文提出了一种无索引的集合最近邻查找算法,并以max函数为例讨论ANN查找算法的实现.
1 基本定义
一般情况下,空间数据库中的数据是均匀分布的.在此前提下,设定f=sum,并以二维空间中的数据为例,分析算法的实现方法.算法很容易推广到高维数据空间,在高维数据空间中也是适用的.
文中一些符号的含义如下:空间数据库数据集P={p1,p2,…,pN};查询数据集Q={q1,q2,…, qn};N,n分别为空间数据库数据集和查询数据集中数据对象的数量;M为最小边界矩形的面积;d(p, q),D(p,q)=|pq|分别为数据对象p,q的距离函数和欧氏距离;集合距离函数adist(p,Q)=f(|pq1|,|pq2|,…,|pqn|),C(q,r)={p|p∈M,|pq|⇐r},S(p)≡S(p,Q)=∪C(qi,|pqi|).
由于空间数据的海量性,因此算法是在没有空间数据索引的情况下,对空间数据进行裁剪,获取一个足够小的查询区域,然后在查询区域中求解ANN.这样可以裁剪掉查询区域以外的数据对象,减少搜索空间,提高效率.如何获得查询区域是算法实现的关键.
首先引入算法中的两个概念:r-近邻域和数据集的最小边界矩形(MBR).
定义1 给定一个查询对象q∈O和一个非负半径r,查询对象q的r-近邻域定义为包含在以q为圆心,r为半径的空间数据点所组成的集合,如图1所示.它可表示为
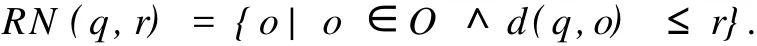
定义2 能够包含查询数据集Q中所有对象的最小矩形,称为查询数据集的最小边界矩形(MBR),如图2所示.
由于空间数据库中的对象是均匀分布的,因此在查询数据集的MBR中总有空间数据库中的对象存在.如图2所示,查询对于f=sum,在数据集P对于查询点集合Q的集合最近邻点将以极大的概率落在Q的MBR中.一般情况下,只需在Q的MBR中查询其集合最近邻点,把Q的MBR以外的区域裁剪掉.这个区域称之为查询区域.
如果一个查询区域足够小,并且又能保证ANN查询结果一定落在该查询区域内时,则称这个查询区域是一个“满意”的查询区域.
2 基于最优点的集合最近邻查找算法
给定一个点p和半径r,将数据空间分成两部分,一部分是p点的r-近邻区域,如图1中的阴影部分;另一部分是p的r-近邻区域以外的区域,称为p的r-近邻外区域.如果半径r足够小,使得p的r-近邻区域刚好能包含查询数据集合Q中的所有对象{q1,q2,…,qn},即p是查询数据集的最小外接圆的圆心,称这个p点为查询集合的最优点,记为vp点,如图1所示.
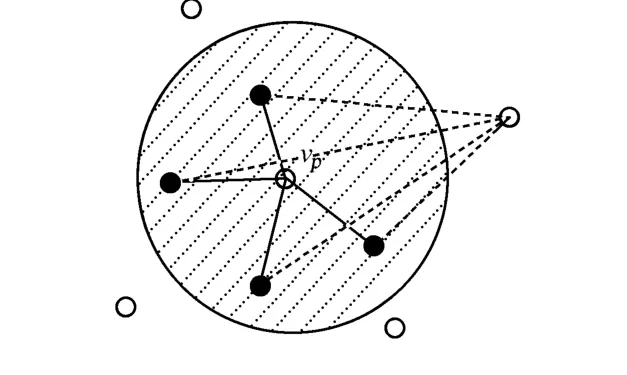
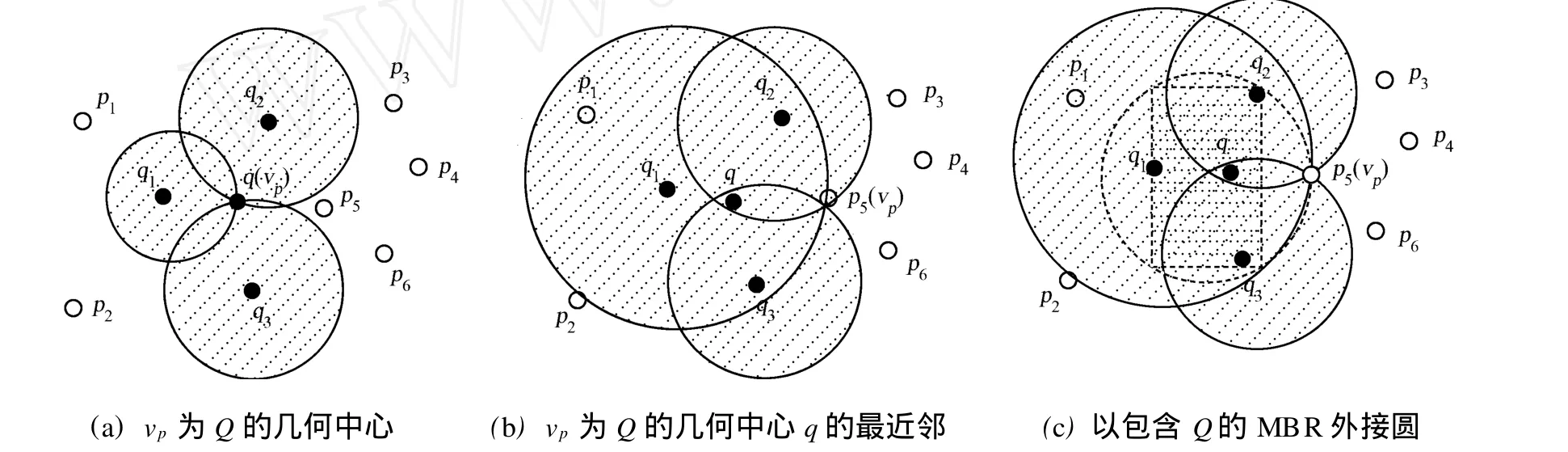
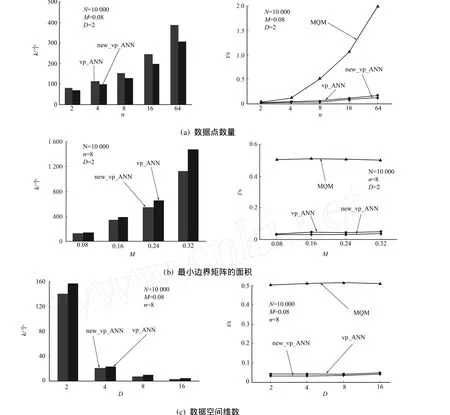
对于f=sum,如果p是Q的集合最近邻点,则p使得adist(p,Q)=sum(|pq1|,|pq2|,…,|pqn|)的值最小.很显然,如果r值合适的话,p一定落在vp的r-近邻区域,而不可能落在vp的r-近邻外区域,即adist(vp,Q) 图1 vp点的r近邻区域Fig.1 Examp le of the r-neighbor region of vp 图2 查询数据集Q的最小边界矩形 Fig.2 M inimum boundary rectangle of query data set Q 图3 r-近邻区域的点集合最近邻比较 Fig.3 Comparison of ANN between he point of r-neighbor and out-neighbor 在vp确定的前提下,寻找合适r的简便方法是,让r=max(|vp qi|)(i=1,…,n).当Q中存在某个对象距离vp点比较远时,求出的查询区域会很大,影响算法的效率.因此,可以采用另一种方法.由于Q的ANN点p使得adist(p,Q)=sum(|pq1|,|pq2|,…,|pqn|)的值最小,故对于每个qi,|pqi|的值应尽可能小,由此可以断定p一定落在每个qi的r-近邻区域.根据定义可知,vp点的r-近邻区域可以表示为C(vp,r)={p|p∈P,|p,vp|≤r}.对于查询数据集Q中的每个对象qi,通过定理1可以求得vp_ ANN算法的查询区域. 定理1 假设Ri=C(qi,ri)表示qi的r-近邻区域,则R=Yi=1,…,n Ri是查询数据集Q中各对象qi的ri-近邻区域的并集.若所选取的每个ri的值能保证Ii=1,…,n Ri不是空集,则Q的集合最近邻点一定落在R中. 根据定理1可知,最优点的集合最近邻查找算法的查询区域就是R.要保证R不是空集,同时又要让R所覆盖的区域尽可能地小,必须合理地计算每个ri的值,而获取合理各个ri值的关键是vp点的选择.因此,vp点的选择是算法的关键. 获取vp点的最简单的方法是随机生成一个vp点,然后取ri=|vp qi|.但是这样做的随机性太大,有可能使R覆盖几乎整个数据空间,使算法失去意义.考虑到f=sum,合理的vp点应该使得adist(vp, Q)=sum(|vp q1|,|vp q2|,…,|vp qn|)的值尽可能地小或者是最小,因此,最佳的vp点应该是Q的质心,P中距离该质心最近的点就是Q的集合最近邻.但是,对于不同的函数f,Q的质心是不一样的. 设(x,y)是Q的质心q的坐标,(xi,yi)为Q中的查询点qi的坐标,为使adist(p,Q)最小,必须满足adist(p,Q)在q(x,y)上的偏导数为0[5].由此可以得出计算q(x,y)的公式,即 然而,上式在n>2的时候没有一个固定形式的解,故利用上式也很难得到所需要的几何中心. 为了降低计算复杂度及提高效率,在基于最优点的集合最近邻查找算法中使用几何中心来代替质心.Q的几何中心q(x,y)的计算公式为 在低维数据空间中,选择Q的几何中心q作为vp点,基本上能保证查询区域R不是空集.但在高维数据空间中,由于数据点比较稀疏,相互之间的距离比较大,可能会导致R是空集,如图4(a)所示.为了避免这种情况发生,算法取数据集P中距离Q的几何中心最近的点作为vp点(图4b中的p5),这样就能保证R中至少有一个vp点,避免了空集的情况,如图4(b)所示.由于R是Q中各个对象qi的ri-近邻区域的并,因此查询区域R总是能包含Q的MBR,这样能保证在空间数据均匀分布的情况下,Q的集合最近邻点总能存在于查询区域R中. 图4 最优点的集合最近邻查找算法查询区域示例Fig.4 Examples of search region by vantage point-bases region pruning algorithm of ANN 基于最优点的集合最近邻查找算法,主要有如下5个步骤: (1)初始化R=Φ; (2)按式(3)计算Q的几何中心,可得到q; (3)在空间数据库P中查找q的最近邻作为最优点vp; (4)查询数据集Q中的每个点qi,再分别计算ri=|qi vp|,Ri=C(qi,ri),并更新R=R∪Ri; (5)在查询区域R中搜索集合最近邻点,并返回结果. 由于空间数据库P中的对象数量要远远大于查询点集合Q中对象的数量,即N≫n.因此在一般情况下,Q中数据点的分布比较集中,基于最优点的集合最近邻查找算法找出的查询区域也会比较小,算法的效率比较高.但是,当Q中数据点的分布比较分散时,对算法效率的影响就比较大.为了提高算法效率,需要对基于最优点的集合最近邻查找算法进行改进,以进一步缩小查询区域,扩大裁剪区域. 当空间数据库中的对象是均匀分布的,对于f=sum,数据集P对于查询点集合Q的集合最近邻点将以极大的概率落在Q的MBR中.显然,在基于最优点的集合最近邻查找算法中找出来的查询区域(图4(c)中的点状阴影区域),不仅一定要覆盖查询点集合Q的MBR(图4(c)中的虚线矩形框区域),而且要比Q的MBR区域大得多.因此,当Q中的数据对象分布比较分散的情况下,可以选取Q的MBR区域作为查询区域. 但是,当Q中的数据对象分布比较集中时,有可能存在Q的MBR区域中没有包含空间数据库P中的对象.此时,如果以Q的MBR作为查询区域,会导致查询区域的数据对象为空集,如图4(c)所示.即p5是Q的集合最近邻点,但它却落在Q的MBR外.因此,将查询区域扩大为Q的MBR的最小外接圆,如图4(c)所示的矩形阴影背景区域,该区域就包含了p5.当然,如果Q中的数据对象分布非常集中,以至于其MBR的最小外接圆中也没有包含空间数据库P中的对象时,可以对外接圆的半径再进行适当的放大,让它足够包含有适当的P中的数据点. 在算法的实现中,查询数据集合Q的最小外接圆的圆心仍然使用Q的几何中心.设qi(xi,yi)(i= 1,…,n)为Q中的点,令min_x=m in_xi,m in_y=m in_yi,max_x=max_xi,max_y=max_yi,i=1,…, n,且(xi,yi)∈Q,则查询数据集合Q的最小外接圆的半径rmin的计算公式为 改进的基于最优点的集合最近邻查找算法,有如下7个主要步骤: (1)初始化R=Φ; (2)按式(3)计算Q的几何中心,可得到q; (3)在空间数据库P中查找q的最近邻作为最优点vp; (4)求Q的数据集的最小边界矩形(MBR),即m in_x=min_xi,min_y=min_yi,max_x=max_xi,max_y=max_yi; (5)计算Q的MBR的最小外接圆,圆心为q,按式(4)计算半径rmin; (6)R=C(q,rmin),当vp点不在R中时,按增量比例d放大rmin,即rmin=rmin×d,d>1,更新R; (7)最后,在查询区域R中搜索集合最近邻点,并返回结果. 在算法的时间复杂度方面,求Q的几何中心的时间复杂度为O(n),其中n为Q中包含的点的数量;求Q的几何中心在P中的最近邻的时间复杂度为O(N),其中N为P中包含的点的数量;求最小包围矩形MBR的左上顶点和右下顶点的时间复杂度为O(n+1);计算MBR的圆心和半径的时间复杂度都为O(1);对集合P的裁剪的时间复杂度为O(N);在裁剪区域R中求AN N的结果的时间复杂度最大不会超过O(N).由于集合P中所包含的数据点一般远远大于Q的中的点,即N≫n,故最优点的集合最近邻查找算法及其改进算法的时间复杂度都近似为O(N). 实验环境:Linux操作系统,Inter(R),Pentium(R),4 CPU,2.66 GHz处理器,512 MB内存;采用C++进行编程.实验数据采用空间数据集P和查询数据集Q,数据集中的数据都经过规范化到(0,1]区间内.实验中,空间数据集P和查询数据集Q都驻留在内存,实验结果数据取50次查询的平均值.数据来源:(1)美国西部地区一些公共地名数据集WUpppoint,包含有10 493个数据点,即它们是一些二维坐标点,数据可从www.rtreeportal.org下载获得;(2)人工随机生成的高维数据,这些数据在数据空间中是均匀分布的. 对不同的n,M及数据空间的维数(D)参数进行分析比较,结果如图5所示.图5中:k为查询区域中数据点的数量,t为CPU执行时间.从图5可知,基于最优点的集合最近邻算法查询区域中的数据点的数量总是比其改进的算法要多,而且随着M和n的增加,查询区域数据点的差别就更大.但是,随着空间数据维数的增加,差别越小.这是因为基于最优点的ANN的查询区域,总是覆盖且大于其改进算法的查询区域,随着维数的增加,数据空间中的数据分布比较稀疏.所以,它们包含的点数的差别就越小. 实验结果表明,所提算法的效率要优于组最近邻居查询算法(M ultip le Query M ethod,MQM),且对于不同的M,n和数据维数D,特别是对于高维数据空间,算法有比较高的稳定性.由于查询区域中数据点的数量比较少,因此,改进的ANN算法的效率总体要比基于最优点的ANN算法要高一点. 图5 不同的查询数据集的算法比较Fig.5 Comparison on the different data set 提出一种无索引的,基于最优点集合的最近邻查找算法及其改进的算法.将算法与其他查询方法进行比较,分析算法的基本特性.结果表明:所提出的算法最大的特点在于不采用任何索引的情况下,也能高效地对空间数据库中的数据对象进行裁剪,缩小查询区域、提高集合最近邻查询的效率.在下一步,将继续研究其他函数的集合最近邻算法,并且将算法扩展到向量空间中. [1]YIU Man-lung,MAMOUL IS N,PAPAD IAS D.Aggregate nearest neighbor queries in road netwo rks[J].IEEE Trans Know l Data Eng,2005,17(6):820-833. [2]JENSEN C S,KOLÁRVR J,PEDERSEN T B,et al.Nearest neighbor queries in road networks[C]∥Proc of the 11th ACM International Symposium on Advances in Geographic Info rmation System s.New Yo rk:ACM,2003:1-8. [3]JA IN A K,M.MURTY N M,FL YNN PJ.Data clustering:A review[J].ACM Comput Surv,1999,31(3):264-323. [4]AGGARWAL CC,YU PS.Outlier detection for high dimensional data[C]∥Proc of the 2001 ACM SIGMOD International Conference on Management of Data.New Yo rk:ACM,2001:37-46. [5]PAPAD IASD,TAO Yu-fei,MOURA TID IA K,et al:Aggregate nearest neighbor queries in spatial databases[J]. ACM Trans on Database Syst,2005,30(2):529-576. [6]PAPAD IASD,SHEN Qiong-mao,TAO Yu-fei,et al.Group nearest neighbor queries[C]∥Proc of the 20th International Conference on Data Engineering.Washington D C:IEEEComputer Society,2004:301-312. [7]L IHong-ga,LU Hua,HUANGBo,et al.Two ellipse-based pruning methods for group nearest neighbor queries [C]∥Proc of the 13th Aannual ACM International Wo rkshop on Geographic Information Systems.Washington D C:IEEEComputer Society,2005:192-199. [8]BEYER K,GOLDSTEIN J,RAMAKRISHNAN R,et al.When is“nearest neighbors”meaningful?[C]∥Proc of the 7th International Conference on Database Theo ry.London:Sp ringer-Verlag,1999:217-235. [9]GU TTMAN A.R-trees:A dynamic index structure for spatial searching[C]∥Proc of the 1984 ACM SIGMOD International Conference on Management of Data.San Francisco:Morgan Kaufmann Publishers Inc,1984:47-57. [10]BECKMANN N,KRIEGEL H P,SCHNEIDER R,et al.The R*-tree:An efficient and robust access method for points and rectangles[C]∥Proc of the 1990 ACM SIGMOD International Conference on Management of Data.New York:ACM,1990:322-331. [11]PAPADOPOULOS A,MANOLOPOULOS Y.Perfo rmance of nearest neighbor queries in R-trees[C]∥Proc of the 6th International Conference on Database Theory.London:Sp ringer-Verlag,1997:394-408. [12]UHLMANN J K.Satisfying general proximity/similary queries with metric trees[J].Information Processing Letters,1991,40(4):175-179. [13]ROUSSOPOULOSN,KELLEY S,V INCENT F.Nearest neighbor queries[C]∥Proc of the 1995 ACM SIGMOD International Conference on Management of Data.New Yo rk:ACM,1995:71-79. [14]ISH IKAWA M,CHEN Han-xiong,FURUSE K,et al.MB+tree:A dynamically updatablemetric index for similarity searches[C]∥Web-Age Info rmation Management.Berlin:Sp ringer,2000:356-373. [15]BRIN S.Near neighbor search in largemetric spaces[C]∥Proc of the 21th International Conference on Very Large Data Bases.San Francisco:Morgan Kaufmann Publishers Inc,1995:574-584. [16]BOZKAYA T,OZSOYOGLU M.Distance-based indexing for high-dimensional metric spaces[C]∥Proc of the 1997 ACM SIGMOD Conference on Management of Data.New Yo rk:ACM,1997:357-368. (责任编辑:陈志贤英文审校:蔡灿辉) An Algorithm of Aggregate Nearest Neighbor Query for Non-Index Spatial Database Luo Yan-min1,2,CHEN Wei-bin1,L IAO M in-hong3 The vantage point-based aggregate nearest neighbor query algorithm and it′s imp roved algorithm are proposed for non-index spatial database in metric space.The algorithms are tested by using both real datasets and synthetic datasets to evaluate efficiencies of the proposed algorithms.The experimental results show that the efficiencies of proposed algorithmsare better than thatofmultiple querymethod.Furthermore,the proposed algorithms have higher stabilization in high-dimensional data space.Since there are less data points in it′s search region,efficiency of the imp roved vantage point-based aggregate nearest neighbor query algorithm is generally higher than the vantage point-based aggregate nearest neighbor query algo rithm. spatial database;nearest neighbor;aggregate nearest neighbor;search region TP 311.131;TP 301.6 A 1000-5013(2011)02-0169-06 2009-08-10 骆炎民(1974-),男,副教授,主要从事图形图像与人工智能的研究.E-mail:lym@hqu.edu.cn. 福建省自然科学基金资助项目(2009J01288)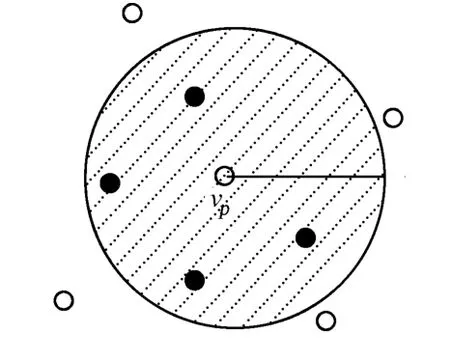

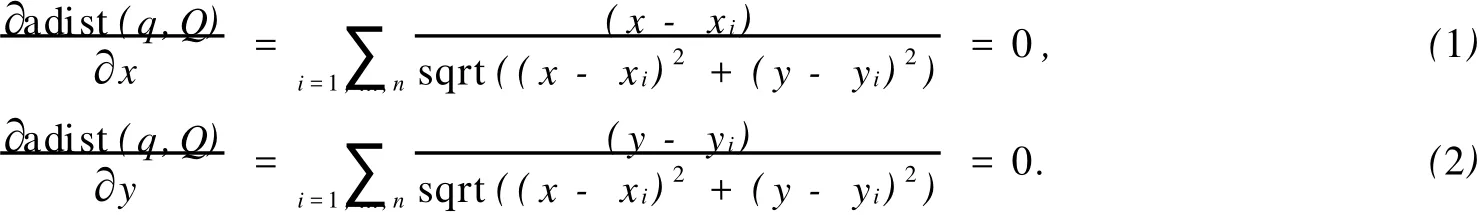
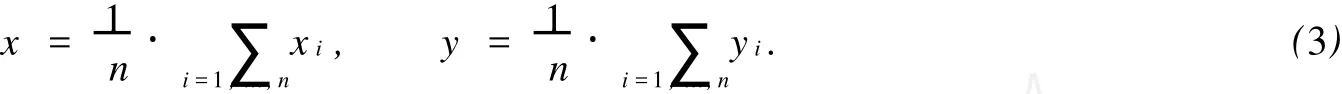
3 基于最优点的集合最近邻查找的改进算法
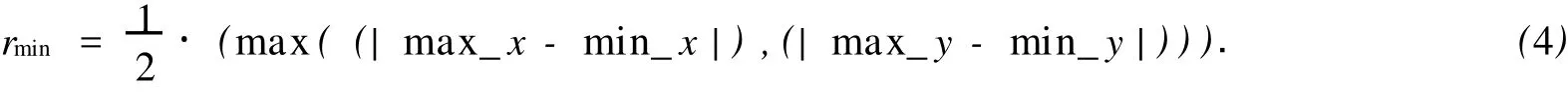
4 算法的分析与实验结果
5 结束语
(1.College of Computer Science and Technology,Huaqiao University,Quanzhou 362021,China; 2.School of Information Science and Technology,Xiamen University,Xiamen 361005,China; 3.School of Software,Xiamen University,Xiamen 361005,China)

