结构参数变化对独塔斜拉桥静力特性的影响

杜蓬娟,孙建刚,谭素杰

（大连民族学院土木建筑工程学院,辽宁 大连 116605）

结构参数变化对独塔斜拉桥静力特性的影响

杜蓬娟,孙建刚,谭素杰

（大连民族学院土木建筑工程学院,辽宁 大连 116605）

独塔混凝土斜拉桥的静力特性主要包括主梁受力及变形、支座反力、主塔受力及变形、拉索受力。通过改变主梁恒载重量、拉索倾角、无索区长度等结构参数,分析结构参数变化对结构受力的影响。分析结果表明,恒载重量增加会使拉索索力呈现线性增加趋势,斜拉索倾角增大对结构的受力有利,但需要考虑主塔高度增大带来的施工难度；无索区长度的增大对结构受力不利。在设计中需要考虑受力和施工的综合影响。

独塔斜拉桥；结构参数；成桥状态

斜拉桥的力学性能指标与斜拉桥的设计参数密切相关,因此,设计参数研究是桥梁设计的重要课题之一。Leonhasdt,Walther等人早在1980年就开展了一些参数研究[1-2],但主要是针对三跨体系。在中国,对斜拉桥参数的研究有的集中在总体参数设计上,有的针对特殊桥型进行分析[3-4]。由于斜拉桥结构体系具有多样性,并且影响因素较多,很难提出一套可普遍接受、严格的评价标准,因此,对该问题的研究不同学者侧重点也是各不相同。本文以已建成的独塔斜拉桥为例,探讨设计参数改变对结构静力特性的影响,该结果可以为独塔斜拉桥的设计提供工程经验和理论依据,为斜拉桥的优化设计提供参考。

1 计算模型及主要假定

在独塔斜拉桥的初步设计阶段,结构形式确定以后,就要初步确定斜拉索倾角范围,确定无索区长度,初步拟定截面高度,确定截面形式,而这些参数的确定都需要丰富的工程经验和理论基础。对于单索面独塔混凝土斜拉桥,由于在设计初就确定了采用拉索在梁中间布置的方案,因此主梁就要选择抗扭能力大的箱型截面。建造在沈阳的公和斜拉桥[5-7],桥面比较宽,宽度达到32m,因此,主梁采用了单箱 5室的截面形式。斜拉索的布置倾角参考了已经建成的桥梁资料,设置在 30°～50°。该桥没有设置较长的无索区长度。

目前对于桥梁的结构分析都是建立在对实际桥梁合理简化后所得模型的基础上进行的,所以结构分析及计算结果的正确与否取决与模型建立的是否合理,是否真实的模拟实际结构,因此,正确建立结构计算模型是进行静力分析与动力分析的首要前提。对于斜拉桥的静力分析,一般将空间结构简化成平面框架来处理,这种简化方法对于单索面结构而言,其计算结果更加准确,当需要了解受力复杂部位时,只要借助于平面框架模型的计算结果建立空间有限元分析模型就可进行该部位的详细分析计算。对于动力分析,一般采用空间结构来模拟,但都需对实际问题进行适当的简化和处理。

以两跨独塔混凝土斜拉桥为例 （如图 1）,根据斜拉桥的结构特点,引入如下假定:1）所有材料符合虎克定律；2）成桥状态采用最小弯曲能量法进行计算[8-10]；3）斜拉索是柔性的,只能受拉。

图1 独塔斜拉桥

2 工程实例及有限元模型

公和斜拉桥位于沈阳市老道口,横跨沈阳站西货场编组站和铁路主干线,是一座双层独塔单索面预应力混凝土斜拉桥。桥的跨径布置为西侧跨径为 114 m,东侧跨径为 120 m,全长为236m。主梁采用单箱 5室断面,横向宽度为 32m,桥梁中心线处梁高为 3.16m,横坡为 1%,箱梁顶板厚为26 cm,底板厚为 24 cm,腹板分别厚 50,38 cm。在主梁上,斜拉索间距为 6.66m,同时 6.66m处设置一道横梁。

主要参数如下:混凝土的弹性模量 E=3.5×107kN·m-2,斜拉索的弹性模量 E=1.95×108kN·m-2,一般主梁截面积为 21.876m2,抗弯惯性矩为 27.63m4,塔根处主梁面积为 30.891 m2,抗弯惯性矩为 44.07 m4。一般主塔截面积为16.078m2,抗弯惯性矩为 25.09m4,主塔根部面积为77.4m2,抗弯惯性矩为 54m4,拉索倾角为 30°。

斜拉桥主梁在平面框架中以二维梁单元来模拟,在斜拉索与主梁相交处设立节点,索与索之间主梁段划分成多个单元。斜拉索与主梁连接通常考虑采用刚臂单元来模拟。斜拉索一般采用桁架单元来模拟,但是桁架单元可以承受拉力也可以承受压力,这与索结构的受力特点不一致,因此,在有限元程序中采用只受拉不受压单元模拟斜拉索。在平面框架结构中主塔采用二维梁单元来模拟,在空间结构模型中,采用三维梁单元模拟,一般在斜拉索与主梁相交处设置节点,同时将索与索之间的主塔划分成多个梁单元。支座可以采用弹簧单元模拟,弹簧刚度根据支座性质确定,也可以根据支座的参数性质设置成梁单元。一般对于扩大基础、沉井基础、锚碇等的处理比较简单,可视为固端。而桩基础的处理比较复杂,常用弹簧刚度等代桩与土的作用。将土视为具有地基系数随深度成正比增长的弹性变形介质。

3 结构参数变化对独塔混凝土斜拉桥静力特性的影响

3.1 恒载变化对静力特性的影响

为了计算方便,在参数变化中只改变一个参数,而其他参数保持不变。恒载按 1.0,1.1,1.2,1.3,1.4,1.5,1.6,2.0倍率变化时,计算了拉索初始张拉力、主梁弯距的变化。在计算拉索初拉力时采用弯曲能量法进行计算。图 2为 1～8号拉索索力与恒载倍率的变化图,从图中可以看出,随着恒载的增加,拉索各索力都逐渐增大,并且拉索索力变化规律一致。图 3为 1～5号拉索索力与恒载倍率变化图,从图中可以看出,随着恒载重量的增大,各根索力的张拉力呈现上升的趋势,并且与自重倍率呈线性关系。

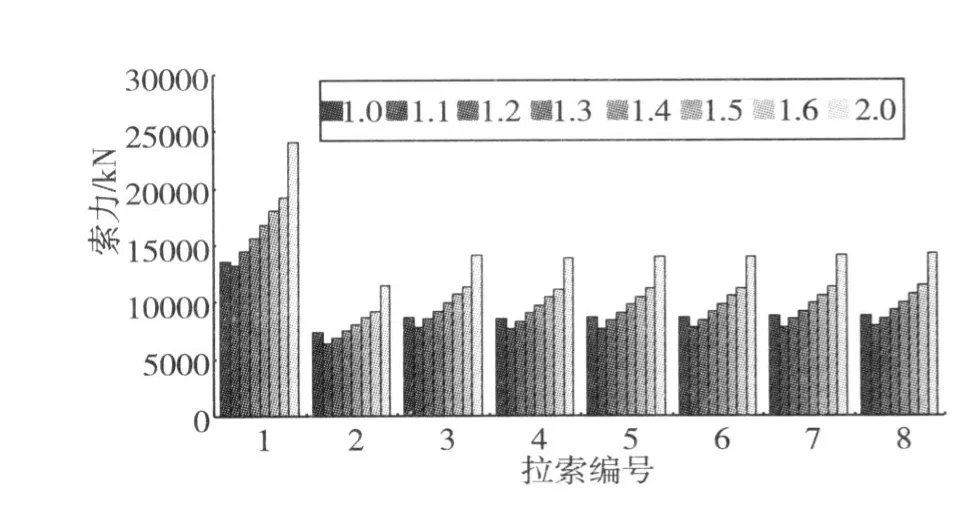
图2 恒载变化对拉索索力的影响

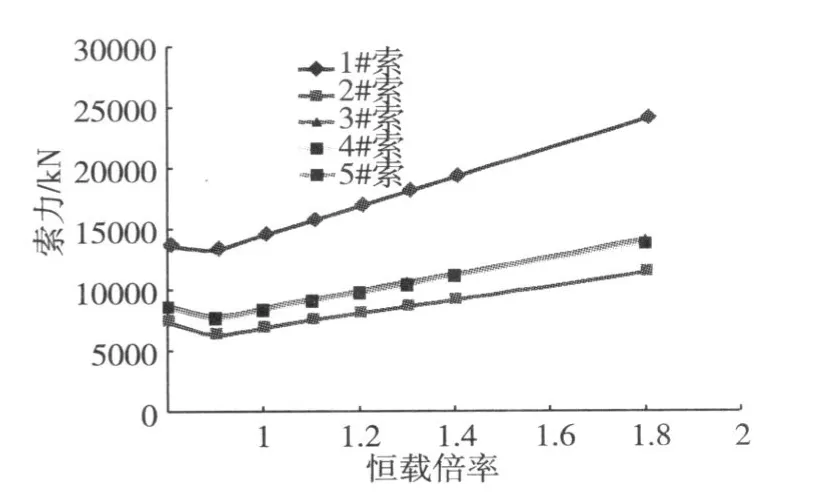
图3 恒载变化对拉索索力的影响

3.2 斜拉索倾角变化对静力特性的影响

为了研究拉索倾角变化对结果受力的影响,在改变拉索倾角中,假定拉索索力保持不变,并保持拉索在主梁上的间距不变,通过改变拉索在主塔上的间距来调整拉索与主梁的倾角。在公和斜拉桥中,拉索水平倾角为 30.45°,为了研究方便,在该角度的基础上乘以一定的倍数,倍数分别为:0.6,0.8,1.0,1.2,1.4,1.6,各倍数所对应的角度分别为:18.27°,24.36°,30.45°,36.54°,42.63°,48.72°。

结构在活载作用下的响应反映了其受力合理程度,因此,在研究斜拉索倾角变化对结构受力影响中以汽车荷载为例。图 4、图 5分别为汽车荷载作用下 130,140,150,160号单元最大正弯矩、最小负弯矩与斜拉索倾角的关系图。从图 4可以看出,对于各单元,随着拉索倾角的增大,弯矩值逐渐减小,弯矩值与倾角倍率的变化呈现出线性变化趋势。从图 5可以看出,各单元负弯矩随着倾角的增大而减小,但绝对值增大。对于同一个单元,单元正弯矩是单元负弯矩值的 2～3倍,因此,斜拉索倾角增大对结构受力有利。

图4 斜拉索倾角变化对单元正弯矩的影响

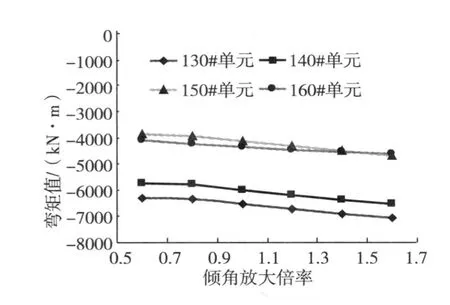
图5 斜拉索倾角变化对对单元负弯矩的影响

图6、图 7分别为汽车荷载作用下左侧支反力最大值与最小值与斜拉索倾角放大倍率的关系。从图 6可以看出,拉索倾角增大,斜拉桥左侧支反力减小,当放大倍数大于 1时,弯矩值呈直线下降趋势。从图 7可以看出,拉索倾角增大,在汽车荷载作用下,该支座处会出现拉力,但拉力值小于500 kN,与出现的压力相比较小,因此,通过综合分析,拉索倾角增大对支座设计有利。

图6 斜拉索倾角变化对最大支反力的影响

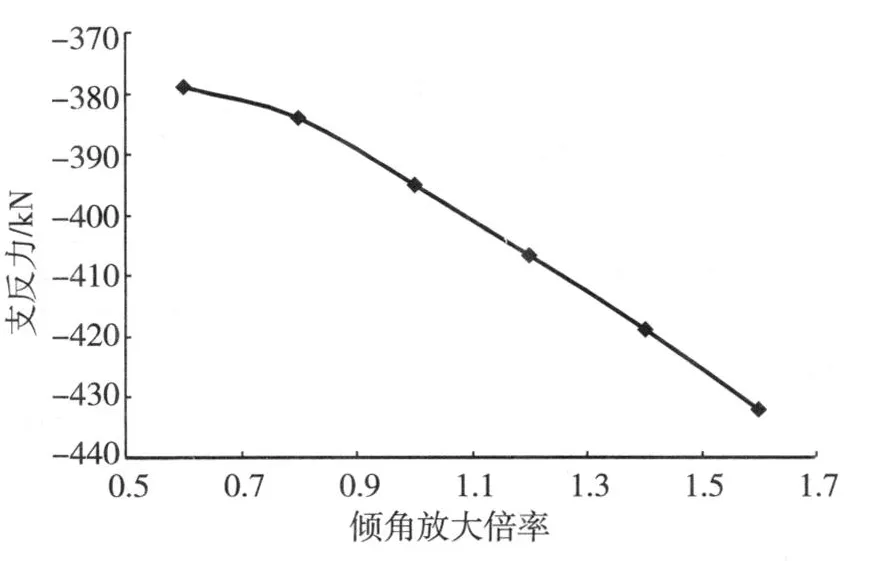
图7 斜拉索倾角变化对最小支反力的影响

3.3 无索区长度变化对静力特性的影响

主梁的无索区长度[11]是主梁上拉索支撑与墩支承之间的一段过渡长度,对于独塔斜拉桥的主跨,有一段或者两段,即主梁近塔处无索区和梁端无索区。近塔处的无索区长度与 0号块长度及施工的方法有关。与近塔处的无索区取值相比,梁端无索区取值差异更大,根据现有独塔斜拉桥梁端无索区长度的统计资料来看,有的主跨梁端不设无索区或者很小。例如贵州的红枫湖大桥,非对称三跨（边跨有 l个辅助墩）,主跨无索区长度为 0；浙江上虞人民大桥,对称双跨,梁端无索区长度为 5m,还不到一个索距。有的独塔体系会存在比较长的无索区,例如辽宁滨海大桥,双跨对称,梁端无索区 10 m；台湾的高屏溪大桥,非对称双跨,主跨无索区长度为 30m。沈阳公和斜拉桥的,左侧梁端无索区长度为 0,右侧 （即东侧）梁端无索区长度为 6.41m,因为该桥基本对称,本文通过改变左侧梁端无索区来研究无索区长度改变对结构受力的影响。左侧无索区长度分别为 0,4.575,6.66,13.32m。

为了分析无索区长度改变对主梁弯矩的影响,本文以汽车荷载作用下的主梁内力图进行比较。图 8—图 11分别为主梁 120号、130号、140号、150号单元处弯矩值与无索区长度的关系,图中主梁弯矩取单元左端点的弯矩值,各主梁弯矩值见表 1。各单元距离梁端的距离分别为24.575,37.895,51.215,64.535m。该区段汽车荷载引起的正弯矩比较大,因此取该区段的数据进行分析。从各图中可以看出,随着无索区长度的增大,120～150号单元处主梁弯矩都增大,近似按照线性规律增大。图 12为单元弯矩值与无索区长度改变的关系图,从图中可以看出,130号单元弯矩值最大,各单元弯矩值与无索区长度接近线性增长。从主梁最大正弯矩受力分析可以看出,无索区长度增大对结构受力不利。

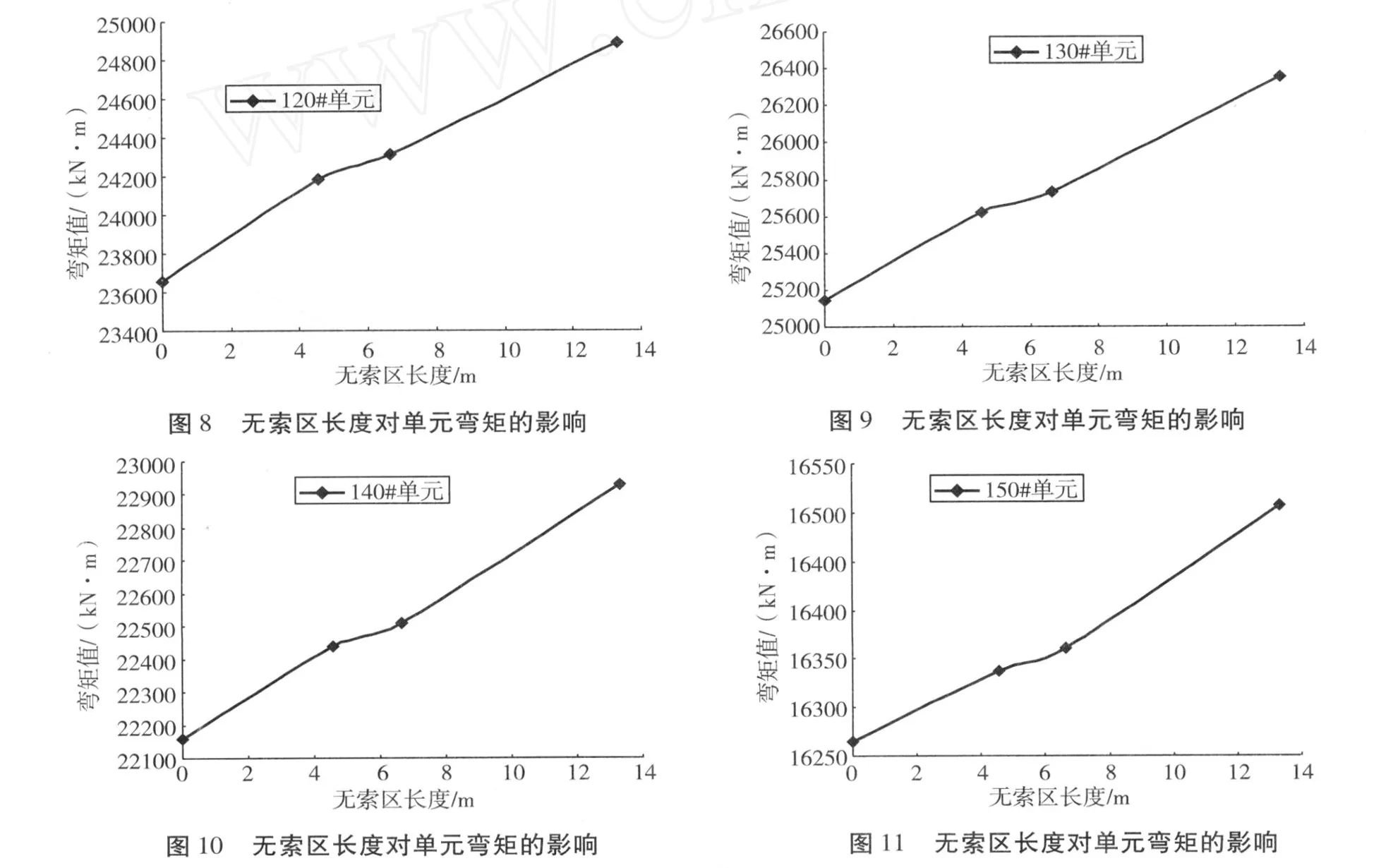
表1 无索区长度对主梁弯矩的影响

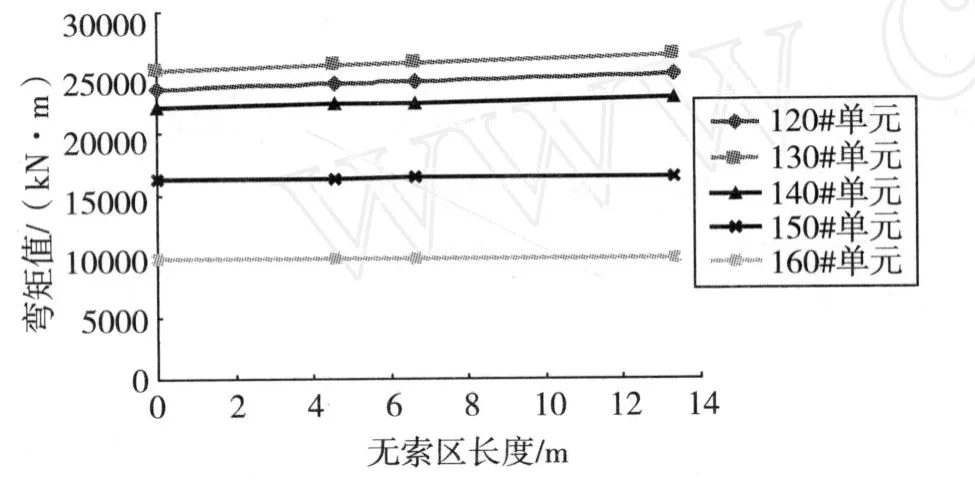
图12 无索区长度对单元弯矩的影响

4 结 论

（1）随着恒载重量的增大,各根索力的张拉力呈现上升的趋势,并且与自重倍率变化呈线性关系。

（2）拉索倾角一般设置在 30°～50°之间,斜拉索倾角增大对结构受力有利。但是由于拉索倾角增大会引起主塔高度的增大,因此,拉索倾角的设置需要综合考虑受力与构造措施。

（3）无索区长度增大对主梁受力的影响集中在主梁靠近边跨侧,总体上分析,无索区增大对结构受力不利,在设计中需要考虑施工因素的影响。

[1]LEONHARDT F,ZELLNERW.Present and future of cable-stayed bridges[C]∥Proceedings of seminar of cable-stayed bridges,recent developments and their future.Japan:Yokohama,1991.

[2]WALTER R.Cable stayed bridge[M]//Second edition.American society of civil engineers,Thom as Telford,Led.,1999.

[3]魏红一.对斜拉桥总体设计参数的讨论 [J].结构工程,2003（3）:1-11.

[4]李冬.独塔斜拉桥参数分析及鸟岛桥施工控制[D].大连:大连理工大学,2006.

[5]杜蓬娟,张哲,谭素杰.斜拉桥施工阶段索力确定的优化方法[J].大连民族学院学报,2006,8（5）:20-23.

[6]杜蓬娟,张哲,谭素杰.斜拉桥合理成桥状态索力确定的优化方法[J].公路交通科技,2005,22（7）:82-84.

[7]杜蓬娟,张哲,黄才良.斜拉桥成桥后误差调整的优化方法[J].哈尔滨工业大学学报,2005,37（7）:1016-1018.

[8]KIM Kiseok,LEEHaesung.Analysis of target config urations under dead loads for cable-supported bridges[J].Computers and Structures,2001（79）:2681-2692.

[9]WANG Paohsii,YANG Chiungguei.Parametric studies on cable-stayed bridges[J].Computers and Structures,1996,60（2）:243-260.

[10]杜国华,姜林.斜拉桥的合理索力及其施工张拉力[J].桥梁建设,1989（3）:11-17.

[11]李晓莉.独塔斜拉桥的设计理论研究 [D].上海:同济大学,2006.

（责任编辑 邹永红）

Parameter Influencing Analysis on Sta tic Characteristics of Single Pylon Cable-stayed

DU Peng-juan,SUN Jian-gang,TAN Su-jie
（College of Architecture＆Civil Engineering.Dalian Nationalities University,Dalian Liaoning 116605,China）

The static characteristics of the single pylon cable-stayed include the internal force and deformation of main girder,reaction force,force and deformation of the main tower.Structural internal force is calculated by changing constant load of the main girder,the cable angle,the length of unsupported deck.The results show s that the cable tension will increaselinearly with the constant load of the main girder,and the increase of cable angle will be benefit.However the construction of tower will be difficult with the height increasing,and it will be bad for structure with the length of unsupported of deck.There fore combined conditions should be considered in design.

single pylon cable-stayed bridges；structure parameter；finished state of cable stayed bridges

U 448.27 < class="emphasis_bold">文献标志码:A

A

1009-315X（2011）01-0041-04

2010-11- 11；

2010-11-11

辽宁省教育厅科学研究计划资助项目（05L061）。

杜蓬娟 （1973-）,女,山西夏县人,副教授,博士后,主要从事大跨度桥梁施工控制理论研究。