节理网络模拟的程序实现及其在地下洞室中的动态响应分析

贾 超，王志鹏，朱维申

（山东大学 土建与水利学院，济南 250061）

1 引 言

随着国内外地下水电站、地下隧道、大型矿山巷道等的大规模兴建，岩石力学的研究重点日益转入地下。在地下工程的建设中，不可避免地要遇到岩体的开挖和处理问题，其中节理岩体是各种岩体工程和环境工程中经常遇到的一种复杂岩体，节理裂隙岩体的稳定性对整个地下工程岩体结构的安全性具有至关重要的作用[1－4]。因此，正确地模拟节理岩体裂隙网络对研究岩体节理裂隙的特征和分布规律具有重要的意义，同时为地下工程的安全稳定性分析提供重要依据[5]。

节理岩体地下洞室在地应力和地震载荷的作用下，失稳破坏的主要形式有[6]：边墙或拱顶的大面积垮塌、大岩块的塌落过度的塑性区产生和相应的边墙大位移、脆性岩体中高边墙出现大深度的裂缝带、突然的岩爆等。这些宏观现象会对工程安全产生极其重要的影响，加之工程开挖所诱发的卸荷裂纹，具有平行于临空面的定向性特征，并经常会滞后发生。目前，国内外对地下洞室的抗震研究还处于探索阶段，在这方面还缺乏系统的研究。因此，研究地下洞室的抗震安全性十分重要。国内学者隋斌等[6]研究了大型地下洞室群在地震荷载作用下的动态响应模拟分析，并采用新的劈裂破坏判据对震后可能出现的劈裂损伤区范围进行了预测。张丽华等[7]采用动力离散元法和模型试验的方法分析了大型岩体地下洞室群的动力响应，认为节理岩体开挖后在地震动力的作用下将加剧块体的运动，进而影响洞室的整体稳定性。李海波等[8]分析了地震荷载作用下埋深、洞室形状等特征对地下岩体洞室位移特征的影响，并得出对工程设计有指导意义的结论。马行东、刘华北等[9－10]研究了地震波入射方向对地下岩体洞室动态响应的影响。

随着计算机技术的发展和普及以及各种数值分析方法在工程地质领域的广泛应用，建立在统计学和概率论基础上的结构面网络模拟技术逐步得到了深入发展。而基于结构面网络模拟结果，开展进一步的数值计算分析，在岩体工程中具有良好的发展前景。本文首先编制了结构面网络模拟分析程序，并将程序生成的可执行数据文件与离散元软件相融合，最后以含节理岩体的地下洞室为例，分别计算了静力和地震荷载作用下，地下洞室围岩在不同时段的应力及位移变化情况。计算方法与结果对含节理岩体地下洞室围岩变形和破坏机制以及抗震工程设计具有指导意义，同时为更进一步研究岩体结构的性质提供帮助。

2 相关基本原理

2.1 节理岩体裂隙网络模拟程序原理

节理岩体裂隙网络模拟的生成过程与现场实测统计过程恰好相反。现场实测统计过程是根据岩体结构形式推求结构面几何参数的分布函数形式及建立结构面的概率模型过程。而计算机模拟形式是上述过程的逆过程，即根据实测统计确立的结构面几何参数的概率模型，求服从这一模型的几何图形。

广泛应用于节理岩体裂隙网络模拟中的蒙特卡罗(Monte-Carlo)方法是一种基于“随机数”的计算方法。它常用于模拟过程中随机数的产生，通过对随机变量的随机模拟和统计试验来反推实际问题的近似解。研究表明，节理岩体结构面的发育具有随机性，各几何特征参数（方位、规模、间距、隙宽等）服从一定的概率分布形式，因此，通过对节理岩体结构面测量数据的分析可以建立各参数的统计概率模型[3]。模拟产生与这个概率模型相似或平行的随机数，再通过抽样统计求出服从这个分布规律的统计估算值，作为分析问题的数值近似解，从而模拟了与实际结构面在统计特征上相同的结构面网络，且在计算机上再现节理岩体结构面的分布形态。

2.2 动力离散元计算原理

在离散元中块体的运动一般采用牛顿第2定律来表示[11－12]，即：

进行中心差分得：

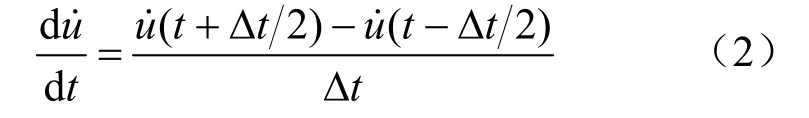
则速度方程转化为

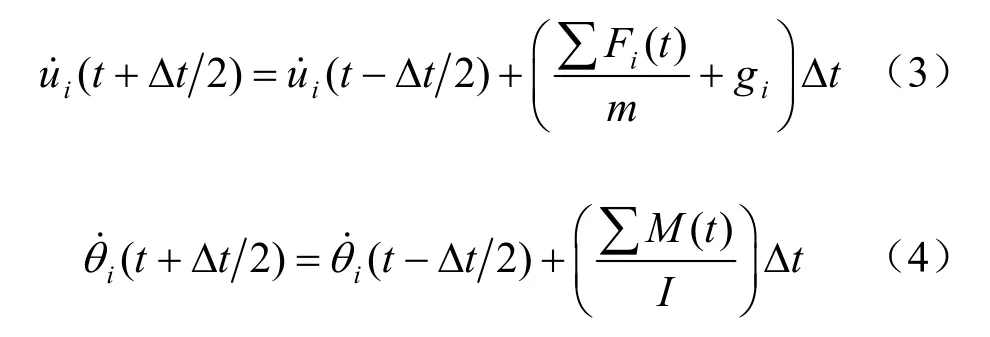
引进阻尼后，动力学基本方程为

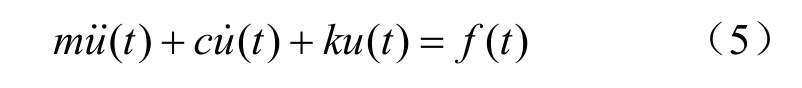
在动力分析中阻尼需要再现对象在承受动力荷载作用下系统能量的损失。对于节理岩体这种材料，自然阻尼一般情况下是滞后的，与路径相关，因此，也就很难用数值方法再现这种阻尼，所以阻尼参数的确定通常采用瑞利阻尼[6,11－12]。

3 程序实现及与离散元的融合

3.1 程序的实现

本文应用岩体结构统计理论及研究成果，在前人研究的基础上，编制了岩体节理裂隙网络模拟分析程序，该程序主要功能及优点如下：

①能够根据需要实时选取参数的分布函数,生成任意概率分布的节理裂隙形态。

②该程序可输出多种格式的数据文件，便于用户将数据结果结合其他软件进行下一步的分析计算。

③在程序调试通过的基础上，运用可视化的VB语言将网络模拟程序进行了扩充与发展，得到了新的可视模拟程序，并且增加了友好的用户界面。

④该程序集成了多种功能，成为一个比较完善的计算程序，并且用户能够容易地使用其操作界面，同时无需再去编译数据文件可有效地减少错误。

该程序的技术路线如图1所示：

图1 节理网络模拟流程图Fig.1 Flowchart of joint network simulation

表1所列为某岩体三组结构面的统计参数，应用本文程序生成的结构面网络图如图2所示，生成的结构面数据信息如图3所示。

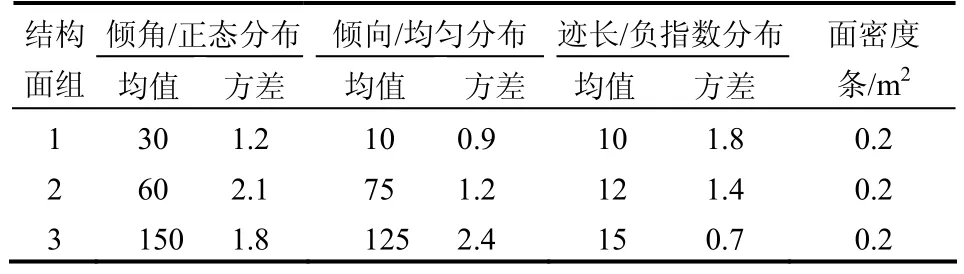
表1 岩体结构面几何参数Table 1 Rock structure surface geometric parameters

图2 节理网络模拟图Fig.2 Diagram of joint network simulation

图3 节理数据信息Fig.3 The data of joints

3.2 程序与离散元软件UDEC的融合

UDEC是基于离散单元法理论的一款计算分析程序。离散单元法最早由Peter Cundall在1971年提出理论雏形，Cundall等在1980年开始又把这一方法思想拓展到研究颗粒状物质的微破裂、破裂扩展、和颗粒流动问题。与有限元技术等通用连续力学方法相比较，属于非连续力学方法范畴的 UDEC程序基于离散的角度来对待物理介质，以最为朴素的思想分别描述介质内的连续性元素和非连续性元素。

该软件特别适合于模拟节理岩石系统或者不连续块体集合体系在静力或动力荷载条件下的响应问题[12]。同时UDEC软件预留了生成节理的外部接口平台，按照UDEC计算程序的要求，将随机节理生成程序结果与UDEC程序进行有机融合，可以进行有效的应用计算，使之更有利于如节理岩体地基、地震、地下结构等问题的分析研究。本文基于结构面网络模拟结果，建立了含节理岩体的地下洞室岩体力学分析模型，然后分别计算了静力和地震荷载作用下，地下洞室围岩在不同时段的应力及位移变化情况。该方法为计算机节理网络模拟结果与工程模型的融合计算提供了参考。

4 算例分析

4.1 计算模型

本文中计算模型为某含节理岩体的地下洞室，洞室平面尺寸为6 m×7.5 m。为体现结构面模拟结果与工程模型的融合计算效果，由本文所编制的程序随机生成了两组节理并融合UDEC软件，生成的模型图以及数值分析中的验算点位置如图4所示。岩体及结构面参数如表2、3所示。

4.2 可变形块体及结构面模型

在数值模拟计算中，地下洞室岩体模型及结构面模型均采用理想弹塑性模型，屈服准则采用Mohr-Coulomb强度准则，屈服函数如下：

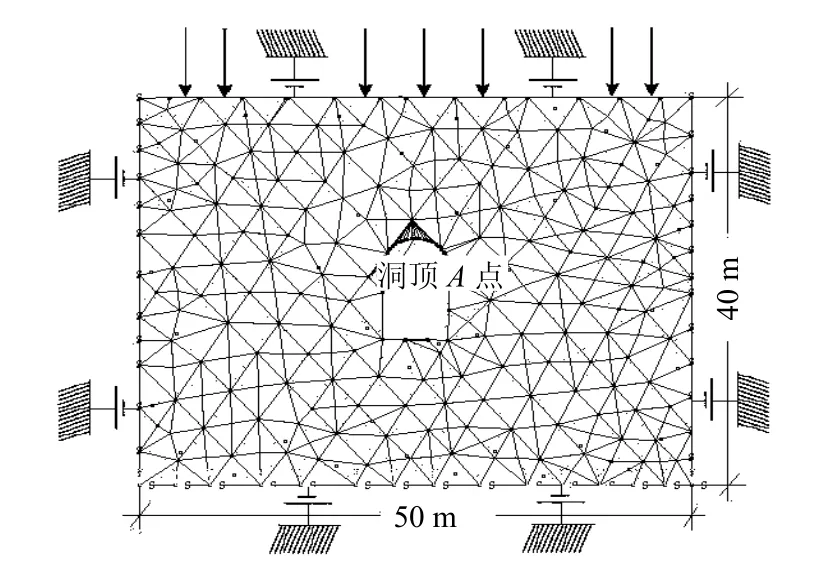
图4 计算模型Fig.4 Computational model

表2 岩块变形和强度参数Table 2 Deformation and strength parameters of rock

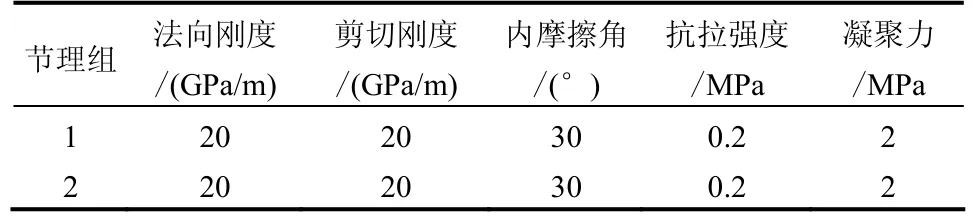
表3 节理变形和强度参数Table 3 Deformation and strength parameters of joints

式中： Nϕ=1 + sinϕ 1 - sin ϕ；其中，ϕ为内摩擦角；σ1、σ3分别为最大和最小主应力；c为黏聚力；σt为抗拉强度。

当岩体内部某一点应力满足 fs＜0，就发生剪切屈服；当岩体内部某一点应力满足 ft＞0，发生张拉屈服。

4.3 边界条件和地震荷载的确定

由于在动力分析中，计算模型的区域边界有可能造成波的反射，给数值分析结果的准确性造成一定影响[13]。因此，在本文模型问题域的外周边界引入黏滞边界用以消除波的反射，从而模拟有限的岩体；考虑到剪切波对洞室响应影响较大，模拟的地震波为施加在模型底面的正弦剪切应力波[8]，其速度时程表征为

最大振幅取1.25 m/s，卓越周期T为1 s，频率为5 Hz，持续时间为2 s，峰值应力为1.25 MPa。由于本文模型边界为黏滞边界，所以速度与加速度不能直接作用在模型边界上，而要转换成应力作用在模型边界上[14－15]，转换公式为

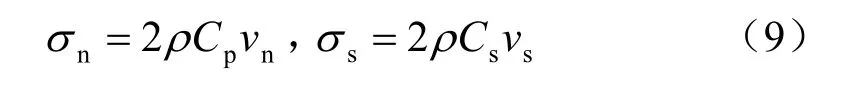
式中：σn为施加的正应力；σs为剪应力；ρ为密度；Cp为传入的p波波速；Cs为传入的s波波速，vn为振动点的垂直速度分量；vs为振动点切向速度分量。

Cp与Cs计算公式分别为

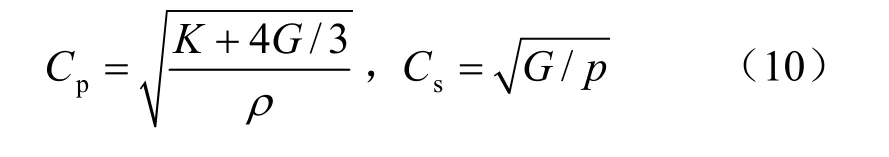
对加速度时程进行积分转化为相应的速度时程，然后由上式转化为相应的应力时程：

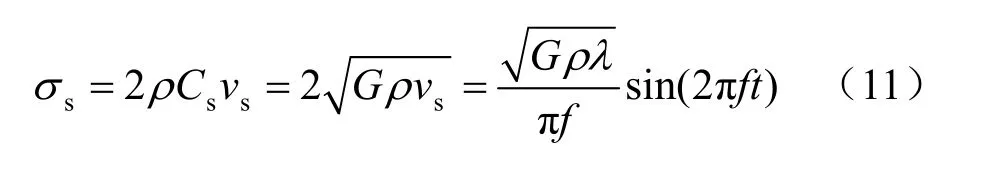
本文阻尼系数采用瑞利阻尼[6,16]，其中质量阻尼系数α=1.57，刚度阻尼系数β=1.59×10-3。

5 计算过程及结果分析

整个数值模拟分为3步。

①在开挖之前，对模型进行固结，形成初始地应力场并且达到平衡状态，初始应力状态按各向同性估计为24 MPa（假定垂直荷载由覆盖深度大约为800 m的岩层产生），固结后，初始地应力场的主应力分布图如图 5所示，初始最小主应力为-26.50 MPa，最大主应力为-19.64 MPa，图中密集分布的部位不是应力集中，而是差分网格密集的部位[7]。

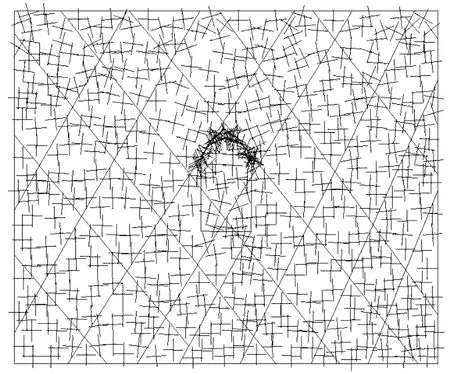
图5 洞室开挖前主应力分布图Fig.5 Principal stress distribution before excavation

②模拟在静力条件下地下洞室的开挖过程。洞室开挖后位移主要发生在拱顶部位，位移矢量图如图6所示，拱顶A点在垂直方向的位移随时间历程曲线图如图7所示，最大位移为10.34 mm，模型最终循环至平衡状态。洞室开挖引起了围岩应力重新分布，主应力分布如图8所示，最小主应力为-53.1 MPa，最大主应力为3.11 MPa，由计算结果可知洞室在开挖后处于稳定状态。

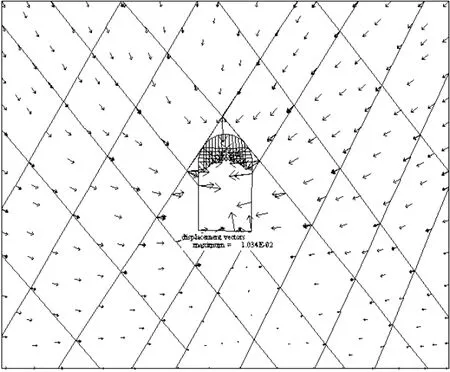
图6 洞室开挖后位移矢量图Fig.6 Displacement vector diagram after the cavern excavation

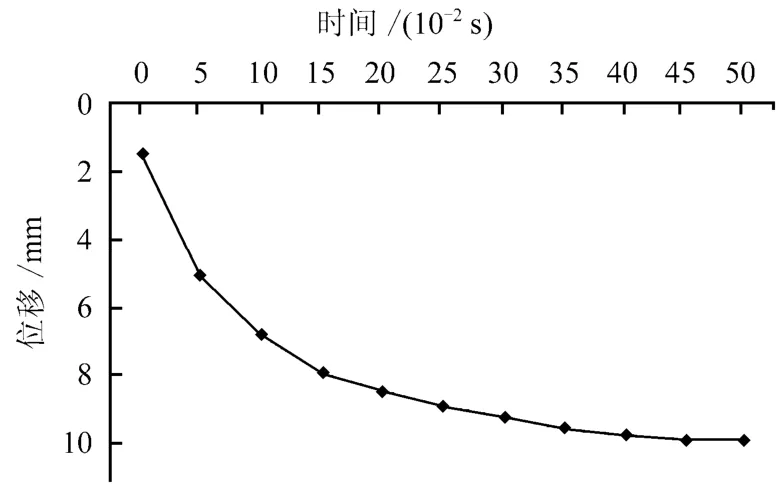
图7 开挖后洞顶A在Y方向上位移随时间历程图Fig.7 Time history responses of displacements of the point A in Y direction after excavation

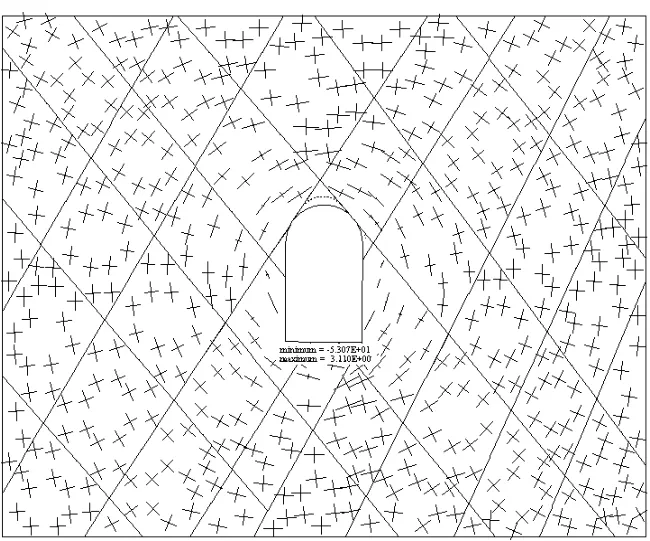
图8 洞室开挖后主应力分布图Fig.8 Principal stress distribution after excavation of cavern

③最后施加地震波，模拟洞室开挖完毕后在动力荷载作用下围岩的位移变化及应力分布情况。由于在动力分析中，计算模型的区域边界有可能造成波的反射，给数值分析结果的准确性造成一定影响[13]。因此，在本文模型问题域的外周边界引入黏滞边界用以消除波的反射；考虑到剪切波对洞室响应影响较大，模拟的地震波为施加在模型底面的正弦剪切应力波。施加地震作用0.02 s后洞室的位移矢量图如图9所示，洞顶A点在垂直方向上的最大位移为 9.12 mm；根据公路隧道施工技术规范(2006-12-25)[17]中规定：当覆盖层厚度大于300 m时隧道周边允许相对位移值为1%～3%，相对位移为实测位移值与两点间距离之比或洞顶实测值与隧道宽度之比。所以在施加地震作用0.02 s后洞室围岩相对位移值为 1.52%，在允许范围之内，洞室此时是稳定的。施加地震荷载后，计算结果显示，洞室的围岩应力发生了重分布，地下洞室的主应力图如图10所示，洞室最小主应力为-53.16 MPa，最大主应力为3.13 MPa。

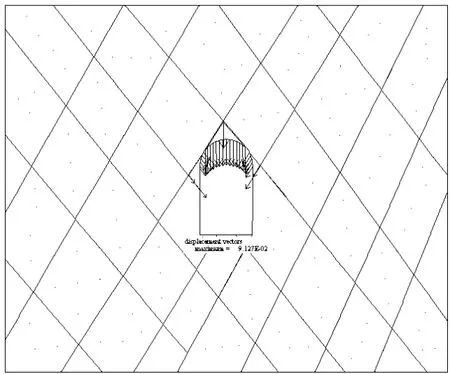
图9 地震荷载作用下0.02 s后洞室位移矢量图Fig.9 The displacement vector diagram of cavern under the earthquake loads after 0.02 s

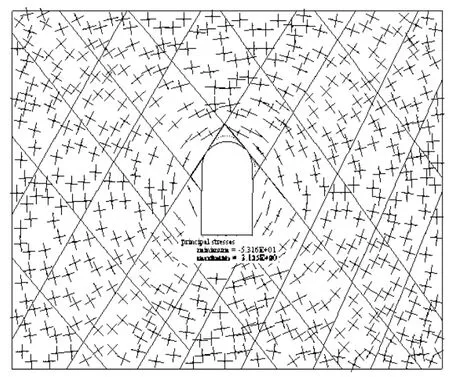
图10 地震荷载作用下0.02 s后洞室主应力分布图Fig.10 Principal stress distribution under the earthquake loads after 0.02 s

施加地震作用0.04 s后，洞室位移矢量图及拱顶 A点在垂直方向的位移随时间历程曲线图如图11、12所示，此时最大位移为242.2 mm，相对位移值为4%，大于允许相对位移值1%～3%，洞室在地震荷载的作用下已经开始破坏。洞室的主应力图如图13所示，洞室最小主应力为-53.24 MPa，最大主应力为3.31 MPa。

计算结果表明，在地震荷载作用下，岩体的结构破坏更加突出。本文所示算例，地震时洞室顶部破坏的后果要远较静力时严重，因此，进行地下洞室的抗震设计时应予以重视。

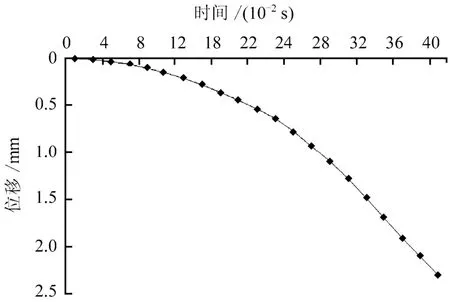
图11 地震作用下洞顶A在Y方向上位移随时间历程图Fig.11 Time history responses of displacements of the point A in Y direction under earthquake loads

图12 地震荷载作用下0.04 s后洞室位移矢量图Fig.12 The displacement vector diagram of cavern under earthquake loads after 0.04 s

图13 地震荷载作用下0.04 s后洞室主应力分布图Fig.13 Principal stress distribution under earthquake loads after 0.04 s

6 结 语

基于结构面网络模拟结果，建立岩体力学分析模型，并开展进一步的数值计算分析，在岩体工程中具有良好的发展前景。本文以含节理岩体的地下洞室为例，分别计算了静力和地震荷载作用下，地下洞室围岩在不同时段的应力及位移变化情况。

计算结果表明：在地震荷载作用下，岩体的结构破坏更加突出。本文所示算例，地震时洞室顶部破坏的后果要远较静力时严重，因此，进行地下洞室的抗震设计时应予以重视。但地震动荷载作用下洞室的位移响应分析是非常复杂的问题，本文基于简单的动力荷载形式和计算模型来分析含节理岩体地下洞室的破坏问题，仅仅是一个初步的探讨，但采用的研究思路及结果对含节理岩体地下洞室围岩变形和破坏机制以及抗震工程设计具有指导意义。

[1]陶振宁. 岩石力学理论与实践[M]. 北京: 水利电力出版社, 1989.

[2]GOODMAN R E. Introduction to rock mechanics[M].New York: John Wiley Sons, 1989.

[3]周维垣. 高等岩石力学[M]. 北京: 水利电力出版社,1990.

[4]黄国明. 节理岩体描述及其工程应用[D]. 成都: 成都理工大学, 1999.

[5]陈剑平. 岩体随机不连续面三维网络数值模拟技术[J].岩土工程学报, 2001, 23(4): 397－402.CHEN Jian-ping. 3-D net work numerical modeling technique for random discontinuities of rock mass[J].Chinese Journal of Geotechnical Engineering, 2001,23(4): 397－402.

[6]隋斌, 朱维申, 李晓静. 地震荷载作用下大型地下洞室群的动态响应模拟[J]. 岩土工程学报, 2008, 30(12):1877－1882.SUI Bin, ZHU Wei-shen, LI Xiao-jing. Simulation of dynamic response of large underground opening complex under seismic loads[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(12): 1877－1882.

[7]张丽华, 陶连金. 节理岩体地下洞室群的地震动力响应分析[J]. 世界地震工程, 2002, 18(2): 158－162.ZHANG LI-hua, TAO Lian-jin. Dynamic response analysis of large underground excavations in jointed rock[J]. World Earthquake Engineering, 2002, 18(2):158－162.

[8]李海波, 马行东, 李俊如, 等. 地震荷载作用下地下岩体洞室位移特征的影响因素分析[J]. 岩土工程学报,2006, 28(3): 358－362.LI Hai-bo, MA Xing-dong, LI Jun-ru, et al. Study on influence factors of rock cavern displacement under earthquake[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 358－362.

[9]马行东, 李海波. 地震波入射方向对地下岩体洞室动态响应的初步分析[J]. 水力发电, 2007, 33(1): 23－25.MA Xing-dong, LI Hai-bo. Primary analysis of different incidence propagation on dynamic response of underground rock cavern under earthquake[J]. Water Power, 2007, 33(1): 23－25.

[10]LIU Hua-bei, Song Er-xiang. Seismic response of large underground structures in liquefiable soils subjected to horizontal and vertical earthquake excitations[J].Computers and Geotechnics, 2005, 32(4): 223－244.

[11]LIN M, KICKER D, DAMJANC B, et al. Mechanical degradation of emplacement drifts at Yucca mountain—A modeling case study—Part I: Nonlithophysal rock[J].International Journal of Rock Mechanics & Mining Sciences, 2007, (44): 351－367.

[12]王泳嘉, 邢纪波. 离散元法及其在岩土力学中的应用[M]. 辽宁: 东北工学院出版社, 1991.

[13]CHEN Jian-yun, JING Li, ZHOU Jing. Seismic analysis of large 3-D underground caverns based on high performance recursive method[J]. International Journal of Solids and Structures, 2004, 41(11－12): 3081－3094.

[14]夏祥, 李俊如, 李海波, 等. 爆破荷载作用下岩体振动特征的数值模拟[J]. 岩土力学, 2005, 26(1): 50－56.XIA Xiang, LI Jun-ru, LI Hai-bo, et al. Blasting vibration characteristics under the load of the numerical simulation of rock[J]. Rock and Soil Mechanics, 2005, 26(1): 50－56.

[15]吕涛. 地下水与地震作用下节理岩体地下洞室围岩力学响应研究[D]. 北京: 北京工业大学, 2005.

[16]王涛, 熊将, 郭武祥, 等. 地震荷载作用下地下厂房围岩稳定的离散元计算方法研究[J]. 长江科学院院报,2005, 26(12): 58－62.WANG Tao, XIONG Jiang, GUO Wu-xiang, et al.Research on stability of rock mass around underground powerhouse cavern by discrete element method under earthquake[J]. Journal of Yangtze River Scientific Research Institute, 2005, 26(12): 58－62.

[17]交通部重庆公路科学研究所. JTJ042－94 公路隧道施工技术规范[S]. 北京: 人民交通出版社, 2006.