一种改进的小波阈值去噪算法及其仿真分析

李永军 马立元 段永刚

(军械工程学院导弹工程系，河北 石家庄 050003)

0 引言

在实际工作中，检测到的信号中都夹杂着各种干扰信号(噪声)，这些干扰信号的存在严重影响了信号本身。为了更好地对信号进行分析，必须进行去噪处理。经实际应用分析可知，信号往往包含许多尖峰或突变部分，且噪声也不是平稳的白噪声，采用传统的傅里叶变换对这种信号进行消噪，效果不明显。而小波变换法由于具有时频局部化、小波基选择灵活、计算速度快、适应性广以及在Besov空间中可以得到任何其他线性估计都达不到的最佳估计等优点，成为信号去噪的一个强有力的工具。

Donoho提出基于阈值处理思想的小波域去噪技术。在小波去噪方法中，阈值法得到了广泛应用。这是因为用阈值法去噪不仅能够最大限度地抑制噪声，而且可以很好地保留反映原始信号的特征尖峰点，去噪效果良好。

1 小波阈值去噪

1994年，斯坦福大学的D.L.Donoho和Johnstone在小波变换基础上提出了小波阈值去噪的概念[1－2]。系统输出信号，即观测信号x(t)可表示为：

式中：s(t)为原始信号;n(t)为高斯白噪声，其服从N(0，σ2)分布。

要把s(t)从x(t)中直接提取出来是比较困难的，需要借助变换方法才能做到。为方便理解，假设信号x(t)为一维信号，经离散采样后，可以得到N点离散信号x(n)(n=0，1，2，…，N －1)。对信号 x(n)作离散小波变换，即：

式中：WTx(j，k)为小波变换系数;ψ()为小波函数;j、k分别为小波变换的分解层数和平移时间。

小波变换，特别是正交小波变换具有很强的去数据相关性，它能够使信号的能量在小波域内集中在一些大的小波系数中，而噪声能量却分布于整个小波域内。因此，经小波分解后，信号的小波系数幅值要大于噪声的小波系数幅值。可以认为，幅值较大的小波系数一般以信号为主，而幅值较小的系数在很大程度上是噪声信号。

Donoho提出的基于阈值的消噪算法(DTA)可以分为以下三个步骤：① 选择小波和小波分解的层数j，计算含噪声信号的小波分解系数;②对每层系数选择一个阈值，并且对高频系数用阈值处理;③根据第j层的低频系数和从第一层到第j层的高频系数，计算信号的小波重构。

小波系数的分解和信号的重构均有成熟的算法及软件程序，去噪的核心是阈值处理方法。

采用阈值的方法可以把信号系数保留，而使大部分的噪声系数减小至零。Dohono提出的阈值去噪方法按照对变换系数进行阈值处理的方法，又可以分为硬阈值法和软阈值法。硬阈值处理首先是把信号小波变换系数的绝对值与阈值比较，小于阈值的小波系数视为零，大于阈值的小波系数不变;然后根据小波系数进行信号重建。软阈值处理是把小波系数大于阈值的变为该点与阈值的差值。

硬阈值处理的数学公式可以表示为：

式中：λ为阈值;djk为小波系数;为处理后小波系数。

软阈值处理的数学公式可以表示为：

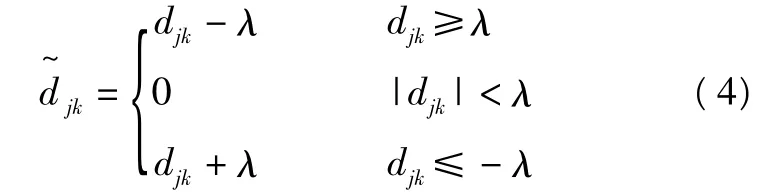
式中：λ为阈值;djk为小波系数;为处理后的小波系数。式(3)和式(4)的图形分别如图1所示。

图1 软硬阈值法曲线图Fig.1 Curves of soft and hard threshold methods

2 新阈值函数的构建

阈值去噪法的关键是阈值函数的构造，阈值函数关系着重构信号的连续性和精度，对小波去噪的效果影响很大。但是硬阈值函数在－λ和λ处是不连续的。这种不连续性导致重构信号容易出现伪吉布斯现象，也就是出现许多不期望的振荡，失去原始信号的光滑性。而软阈值函数虽然整体连续性好，但估计值与实际值之间总存在恒定的偏差，并且软阈值函数的导数不连续，具有一定的局限性[6－7]。为了克服这些缺点，文献[3]提出了软硬阈值折衷法[3]，其数学表达式为：

该方法在阈值估计器中加入了α因子，0≤α≤1。适当调整α的大小，可以获得较好的去噪效果。软硬阈值折衷法的函数曲线如图2所示。

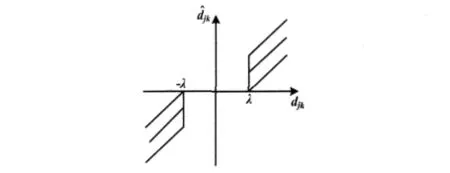
图2 软硬阈值折衷法函数曲线Fig.2 Curves of the compromise soft and hard threshold methods

为使阈值函数更加灵活，本文提出了一种新的阈值函数——开方法。我们先考虑djk＞0的情况，设：

由式(6)可知，当djk＞＞λ时，接近于 djk，系数 n为接近速度系数，n越大，其接近速度越快。对上式进行改写，即：

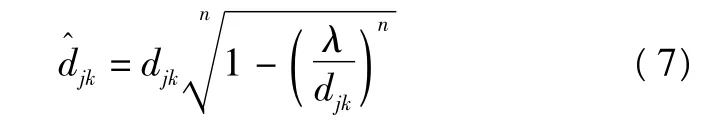
对于一般情况，有：

因此，该方法的函数表达式为：

开方法曲线如图3所示。

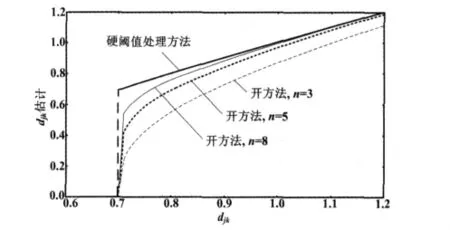
图3 开方法曲线Fig.3 Curves of the extraction method

由于当n增大时，函数接近硬阈值处理函数;当n减小时，函数接近软阈值处理函数。因此，根据这一特点，可以得出参数n选择的原则是：当待降噪信号中包含了大量的同性区域或要求降噪后信号有尖锐的突变时，应使阈值向硬阈值方向移动，即n的取值比较大，一般可选在2左右;而在信号比较平滑的情况下，应使阈值向软阈值方向移动，即n的取值在0～2之间。按照这一原则适当调整n的大小，可以获得更好的去噪效果。

3 仿真分析

为了验证本文提出的阈值处理方法的有效性，在Matlab平台下对不同去噪方法进行仿真试验。对应于特定的含噪信号，不同的小波基会产生不同的消噪效果。这是小波方法进行信号消噪中的一个关键问题。

小波基的选择和小波基的类型有关。在同一待降噪信号中，既有比较平滑的区域，又有突变的区域。在平滑区域中，一般采用高正则阶、高消失矩的光滑小波基函数。因为选择具有较高阶消失矩的小波函数，能检测信号中更精细的奇异性，所以在重构时，信号中的细节才能更多地得到恢复。

在突变区域中，要采用紧支撑的小波基。Daubechies基是具有紧支集的光滑正交小波基，小波的光滑性由其支集的长度N来确定，通过合理选择N值的大小，既可以简化计算的复杂程度，又保证了信号分析中的空间局部化要求。

Daubechies小波基函数使得内积计算快、基函数叠加快，其良好的空间局部化和良好的频率局部化，在保证了信号展开和重构的低复杂度的同时，又保证了信号中主要成分和模式的识别。借用基和算法来进行信号小波变换处理是一种有效的方法。这里采用Daubechies作为小波基函数。

本文选取了Bumps信号和Blocks信号两种Matlab中常用的信号作为原始信号[4－5]。

为模拟实际信号，向两种信号中加入噪声，噪声方差为 0.1，其中输入 Bumps含噪信号的信噪比是15.343 dB，Blocks 含噪信号的信噪比是 17.504 dB。分别用传统的软硬阈值法和文献[3]提出的软硬阈值折衷法与文中提出的开方法阈值法进行了去噪处理。分解层数为5层，开方法阈值法中的n取为1.8。

对于阈值的选取，Dohono等人曾给出通用阈值的选取，但在有些应用过程中发现该阈值并非十分理想，还需根据具体情况对其作一定的改进。阈值主要由噪声方差的估计值和子带系数的能量分布共同确定，大部分情况下，需要从观测数据中估计噪声方差。如果阈值λ选取过小，去噪后的信号仍然有噪声的存在，造成去噪不完全;反之，如果阈值λ选取过大，部分有用信号将被误认为噪声而被滤掉，引起偏差。由于噪声的小波变换系数随着尺度的增大而减小，对信号进行去噪时，不同的分解层阈值的选取应该有所不同，并且随分解尺度的增大，阈值应该有所减小。

本文采用文献[3]给出的方法，即针对不同的分解尺度j，给出阈值的选取方法1)，其中，N为相应层的小波变换系数的个数，σ为噪声方差。更加合适的阈值选取方法有待于今后进一步的研究。

Bumps和Blocks的原信号与含噪Bumps和Blocks信号时域图如图4所示。

图4 Bumps和Blocks原信号与含噪信号时域图Fig.4 Time domain graphic of Bumps and Blocks original signal and noising signal

经试验可知，这几种方法都能去除大部分的噪声信号，其中，硬阈值方法残留噪声最多，软阈值去噪比较平滑，但其对原始信号中突变的重现不够。开方法在平滑度上要优于软硬阈值折衷法和硬阈值法，比软阈值法略差，但在突变信号的保留上明显优于软阈值法。

两信号分别采用不同阈值处理方法进行处理的结果如图5所示。

图5 各阈值处理方法去噪结果Fig.5 Results of each threshold processing method

为了能够对分析结果进行量化，本文对几种方法进行了500次仿真分析试验并统计平均，得到各方法的信噪比(SNR)和均方差(MSE)如表1所示。

从表1可以看出，文献[3]的方法和本文提出的方法去噪效果均优于软阈值法和硬阈值法，开方法的效果略优于折衷法。

表1 SNR和MSE比较Tab.1 Comparison of SNR and MSE

4 结束语

本文针对Donoho和Johnstone提出的软硬阈值去噪方法的缺点，构造了一种新的阈值函数，并对其进行分析，最后通过仿真试验将该方法与传统的硬软阈值法和文献[3]提出的软硬阈值折衷法进行了比较。从试验数据上可以看出，本文的开方去噪方法在进行去噪处理时，在信噪比增益和最小均方误差意义上均优于传统的软硬阈值法和软硬阈值折衷法。试验结果表明，新方法兼顾了软硬阈值法的优点，在去噪效果上要优于以上三种方法。但由于该方法的参数n的确定需要一定的经验判断，所以在使用时可能需要多次的试验进行比较，以确定n的最佳取值。

[1]Donoho D L.Denoising by soft-thresholding[J].IEEE Transactions on Information Theory，1995，41(3)：613 －627.

[2]Donoho D L，Johnstone I M.Adapt to unknown smoothness via wavelet shrinkage[J].Journal of the American Statistical Association，1995，90(432)：1200 －1224.

[3]赵瑞珍，宋国乡，王红.小波系数阈值估计的改进模型[J].西北工业大学学报：自然科学版，2001，19(4)：625 －628.

[4]胡昌华，李国华，周涛.基于MATLAB 7.X的系统分析与设计——小波分析[M].3版.西安：西安电子科技大学出版社，2008.

[5]李祥兵，肖合林.基于 Matlab的小波阈值折衷去噪算法研究[J].电脑开发与应用，2009，22(6)：4 －6.

[6]陶红艳，秦华峰，余成波.基于改进阈值函数的小波域去噪算法的研究[J].压电与声光，2008，30(1)：93 －95.

[7]朱艳芹，杨先麟.几种基于小波阈值去噪的改进方法[J].电子测试，2008(2)：18－22.