InSAR卫星编队构型的e/i矢量设计方法

杜耀珂,阳 光,王文妍

(上海航天控制技术研究所,上海 200233)

0 引言

编队飞行时,2个或更多卫星在各自围绕地球运动的同时,彼此间形成特定形状的卫星编队。因各卫星间隔距离较近,密切联系、相互协同,相当于一个巨大的虚拟卫星。卫星编队因其灵活性,不仅能实现一颗大卫星难以完成的任务,而且可降低单颗大卫星的复杂度,节约研制成本,并提高整个系统运行的可靠性。编队InSAR利用了编队卫星的相对轨道构型特性,突破了传统SAR卫星只能平面测量的局限性,可获得观测目标的高程信息。为实现上述功能,设计满足要求的编队构型是编队SAR的关键。目前,对编队设计研究大多基于星下点圆形和空间圆形等典型编队构型[1]。这些典型编队构型的设计方法以编队飞行动力学约束条件为基础,利用卫星间形成的空间基线,调整编队构型设计参数,以获得性能尽量好的编队构型。但SAR卫星编队设计要求满足垂直基线和沿航迹基线的位置要求,另外为实现要求的观测精度,对SAR干涉工作时卫星的空间距离也提出了要求[2]。这些都是典型编队构型未加考虑的。为此,本文针对SAR卫星编队的特殊要求,用e/i矢量表示的编队运动学方法设计了SAR卫星编队构型。

1 编队坐标系与测量基线定义

1.1 编队飞行坐标系

定义编队坐标系如图1所示。图中：原点为参考卫星的中心或参考点;ox轴为地心至参考卫星的矢量方向;oy轴为参考卫星速度方向,垂直于ox轴;oz轴与ox、oy轴构成右手坐标系,与卫星角动量方向一致;Sa为伴随卫星。

图1 编队卫星的坐标系Fig.1 Coordinateof formation flying satellites

1.2 量基线

测量基线分为垂直基线和沿航迹基线。为说明垂直基线,需了解卫星视线方向的定义。卫星视线方向是卫星的SAR天线对地观测时的观测方向。编队飞行的垂直基线是指2颗卫星在垂直于速度平面(xoz面)内的距离在垂直卫星视线方向的投影长度,如图2所示。图中：Sr为参考卫星;Sa为伴随卫星在平面xoz内的投影点;虚线为卫星的视线方向,视线方向位于平面xoz内,与ox轴的夹角为ξ;垂直基线B⊥为Sr与Sa的连线在垂直视线方向的投影。沿航迹基线即为参考卫星在编队飞行坐标系中的oy轴向的长度。

图2 垂直基线Fig.2 Vertical measurement baseline

2 e/i矢量法实现及其优点

2.1 e/i矢量法引入

为描述伴随航天器(下标2)相对参考航天器(下标1)的相对运动,定义相对轨道根数的矢量Δα。用半长轴ak、偏心率ek、轨道倾角ik、近地点辐角ωk、升交点赤经Ωk和平近点角Mk分别表示两卫星的Kepler轨道根数(k=1,2),相对偏心率矢量和相对倾角矢量分别为

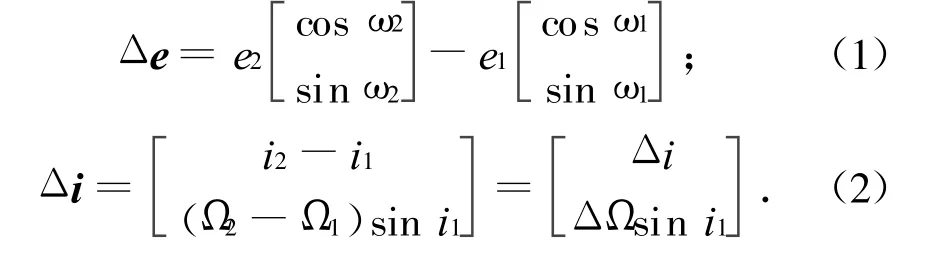
另设

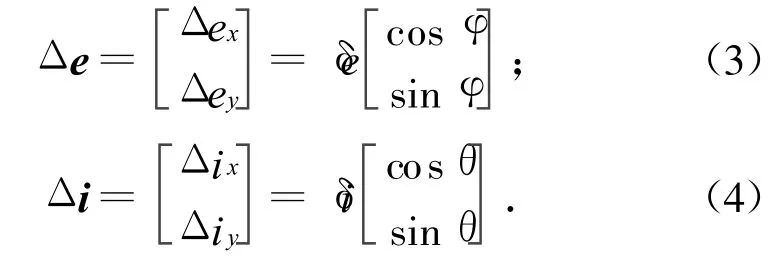
式中：δe,φ分别为Δe的大小和相位;δi,θ分别为Δi的大小和相位,其几何意义如图3所示。图中：N1,N2为轨道的升交点;N12为两个轨道的交点(相对升交点)。

图3 两星紧密编队的轨道关系Fig.3 Two closing formation satellites'orbit

根据上述定义,相对轨道要素可表示为

本文中,纬度辐角u=ω+M,这时因为在近圆轨道中用纬度辐角表示的效果较平近点角更佳[3]。用半长轴乘以角度差值直观表示编队构型。为使编队卫星有相同的轨道周期,2颗卫星的轨道半长轴应相同,故下文用a替代a1。

2.2 e/i矢量法描述相对运动

设计构型时,需根据基线要求寻求符合要求的一组轨道参数,因此要获知轨道参数与编队构型的关系。

根据SAR卫星特点,一般要求构型大小为约2 km,属于紧密编队构型,因此2颗卫星的间距较小,且SAR卫星一般采用近地、近圆(小偏心率)轨道。因此,根据编队卫星的位置关系(图3)推导对伴随卫星相对参考卫星的相对运动学方程如下[4-5]。

设Sa在编队坐标系中的坐标为(x,y,z)。在球面三角形SrSaN12中,令SrSa对应的圆心角为β,由正弦定理可得：sin(u2-θ)=。因SrSa相对a很小,故β是一很小的角度,可认为sinβ≈z/a。则

由于两星为紧密编队构型,可认为两星的纬度辐角相等。取参考卫星的纬度辐角为u,则伴随卫星在oz轴向的运动可表示为

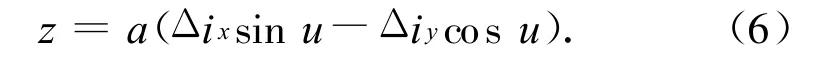
在运动方向上,考虑近地SAR卫星的偏心率一般很小,如取e的一阶项而忽略其高阶项,则可得

故有

两颗卫星取差分,可得

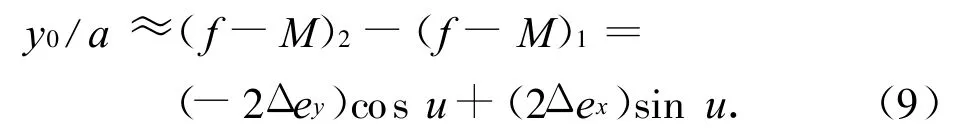
再考虑由升交点赤经引起的在运动方向上的位置差异

综合式(9)、(10),可得在卫星运动方向上相对运动

在轨道面内,矢径方向同样只取e的一阶项,则可得

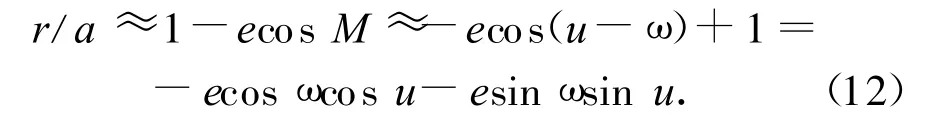
两颗卫星取差分,即由

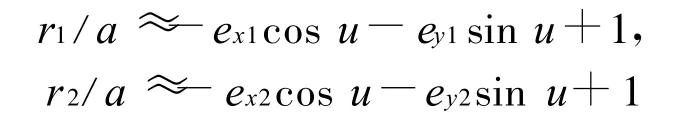
取差分,可得

综合式(6)～(13),可得用e/i矢量法描述的卫星的相对运动方程

根据式(14),在获知编队飞行的几何构型后,易将几何构型转换为卫星的轨道参数。

3 InSAR卫星编队设计

某InSAR任务对编队构型要求为：保证在In-SAR测量工作区间,有效基线长度B⊥为1 000～2 000 m,沿航迹基线长度小于500 m;工作时的星间距离小于2 000 m。

在近地卫星中,由于地球非球形摄动的影响,卫星的Ω会缓慢漂移,漂移速度与a,i有关。在编队飞行中,编队卫星的a相同,如能保证i相同,则各卫星的Ω漂移速度相同,也就避免了编队任务中对Ω的控制,可显著节省燃料。因此,本文设计采用等轨道倾角的编队设计方法。

由式(14)可知：相对运动在平面xoy内为椭圆,但中心不在原点。当补偿掉y向的常量部分Ly=a1ΔΩcos i1后,绕飞编队的构型可简化成为

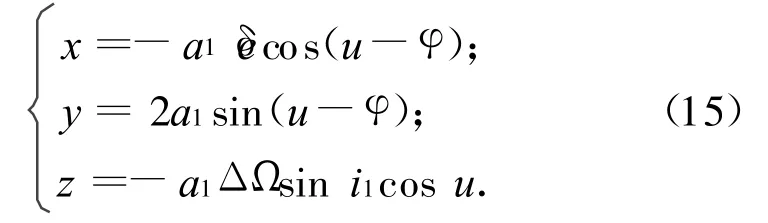
为便于描述相对位置关系,令p=a1δe,s=a1ΔΩsin i1,θ=-φ,θ-α=-π/2,则式(15)可改写为

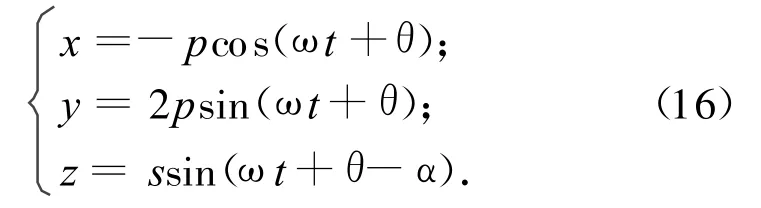
p,s,θ的几何意义分别如图4、5所示(取s＞p＞0)。令卫星初始位置位于升交点,θ为平面xoy内的初始相位角。其中：取视线角ξ=33°。

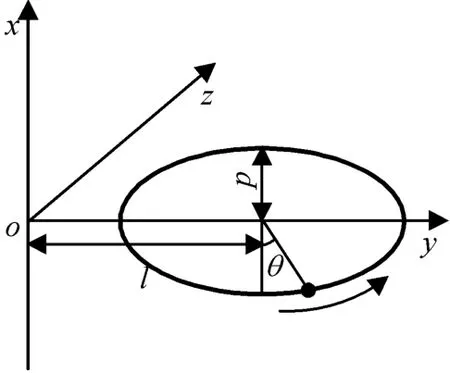
图4 编队构型参数意义(xoy面内)Fig.4 Meaning of f ormation flying parameters in plane xoy

图5 编队构型参数意义(xoz面内)Fig.5 Meaning of formation flying parameters in plane xoz

由式(15)、(16)可知：参数p,s,θ,α确定了编队构型,同时根据这4个参数也能反算出相对轨道参数。因此,编队构型的设计就是寻求满足编队构型的上述4个参数,并将上述参数转换为轨道参数。

假定从该位置开始满足测量要求,考虑对航向基线的限制B‖≤500 m,因航向的构型大小为2p,为满足航向基线要求,且使p值不至于太小而产生x向过小的构型(会增大碰撞的可能性),可得θ的取值范围为180°或0°附近,即有θ=0°-Δθ,θ=180°-Δθ两种情况。此处：Δθ为正值的一小角度。

在平面xoz内,因z=-a1ΔΩsin i1cos u,即起始位置必然位于z=-s位置,即在oz轴负向最大位置。取θ在0°,180°附近两种情况作出平面xoz投影,分别如图6、7所示。

图6 θ=144°时xoz面内的投影Fig.6 Projection of relative orbit in plane xoz whenθ=144°

图7 θ=324°时xoz面内的投影Fig.7 Projection of relative orbit in plane xoz whenθ=324°

由图6、7,综合对基线的要求,取构型1的参数为：p=400 m;s=1 880 m;α=60°;θ=330°。构型1实现的基线和距离分别如图8、9所示。

图8 构型1的基线Fig.8 Vertical baseline of shape 1

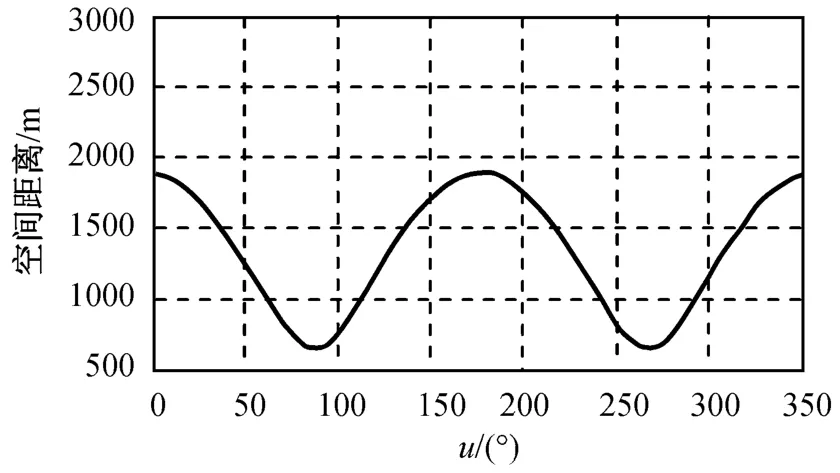
图9 构型1的空间距离Fig.9 Relative distance of shape1

可见,在满足观测条件的纬度辐角范围为0°～57°。为实现全球观测,至少要能覆盖纬度辐角范围为0°～90°,这样在对称的位置可覆盖南半球的纬度范围。因此,考虑基于述构型,根据以上原则,获得在高纬度覆盖构型的参数为：p=1 050 m;s=3 150 m;α=157°;θ=67°。由此可得构型1实现的基线和距离分别如图10、11所示。

满足覆盖条件的纬度辐角范围为100°～125°,对近地太阳同步轨道卫星(i约97°),基本能实现南北纬80°的全球覆盖要求。

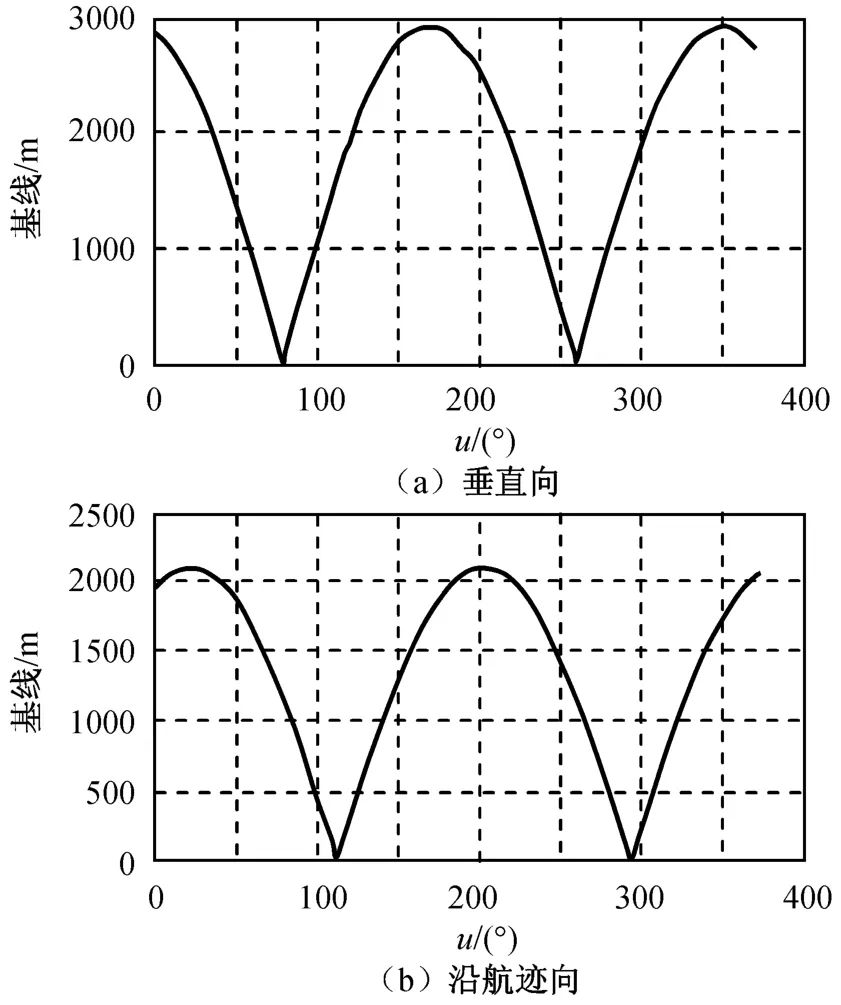
图10 构型2的基线Fig.10 Vertical baselineof shape2

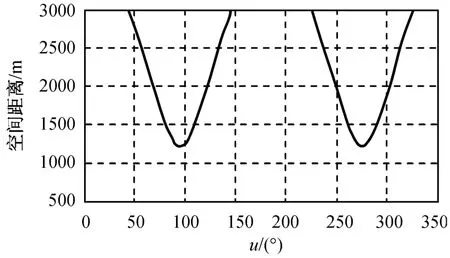
图11 构型2的空间距离Fig.11 Relativedistance of shape 2

4 仿真

根据式(14)、(15)和构型1、2参数,给定参考卫星Sr的轨道参数,可得两种构型的伴随卫星轨道参数见表1。用表1的轨道参数进行仿真,时间为1个轨道周期,所得可进行观测的纬度范围及对应的星下点纬度关系分别如图12～15所示。

表1 两种构型的编卫星轨道参数Tab.1 Orbit elements of f ormation flying satellites with two shapes

在满足InSAR测高的基线与相对距离要求的前提下,用两种编队构型就能基本实现对南纬80°至北纬80°之间地区的高程测量。仿真结果也表明：轨道构型1能够覆盖南纬58.2°～北纬58.1°的观测范围;轨道构型2能覆盖南纬56.9°～77.8°和北纬56.8°～77.8°的观测范围。

图12 构型1覆盖的纬度与垂直基线范围Fig.12 Latitude coveragerangeand vertical baseline rang of shape1

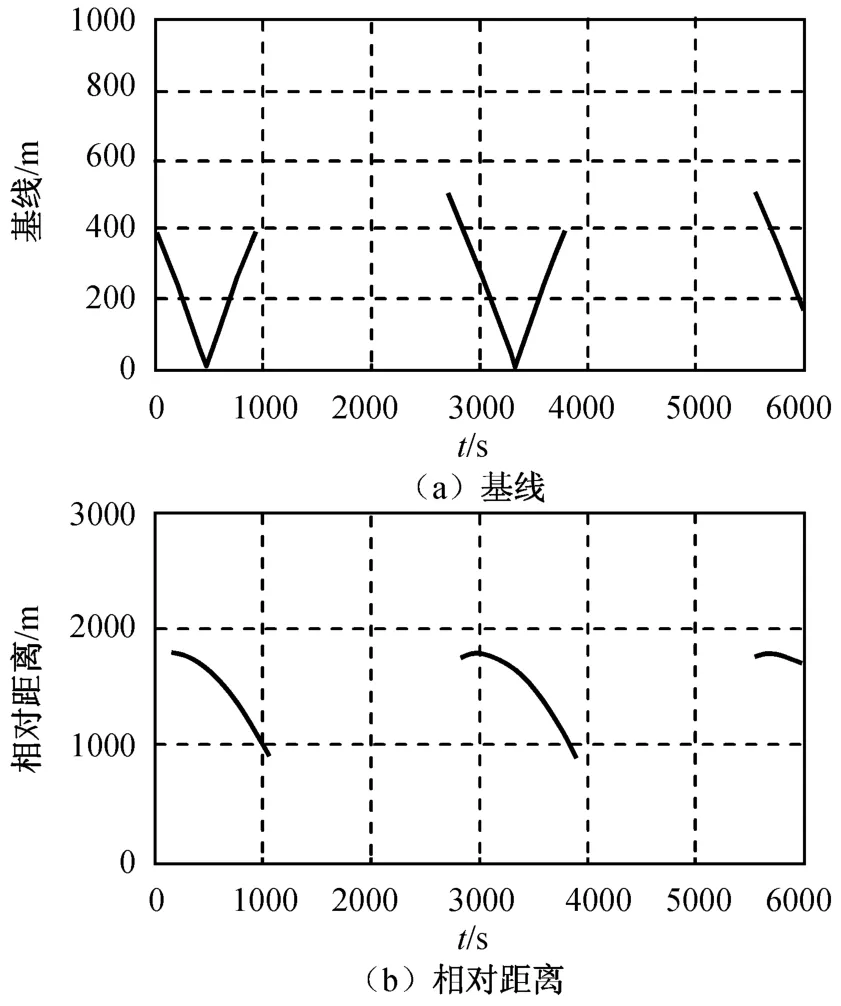
图13 构型1航迹基线范围和两星的相对距离Fig.13 Flying direction rang and two satellites'relative distance of shape1

图14 构型2覆盖的纬度范围和垂直基线范围Fig.14 Latitudecoverage range and vertical baseline rang of shape 2

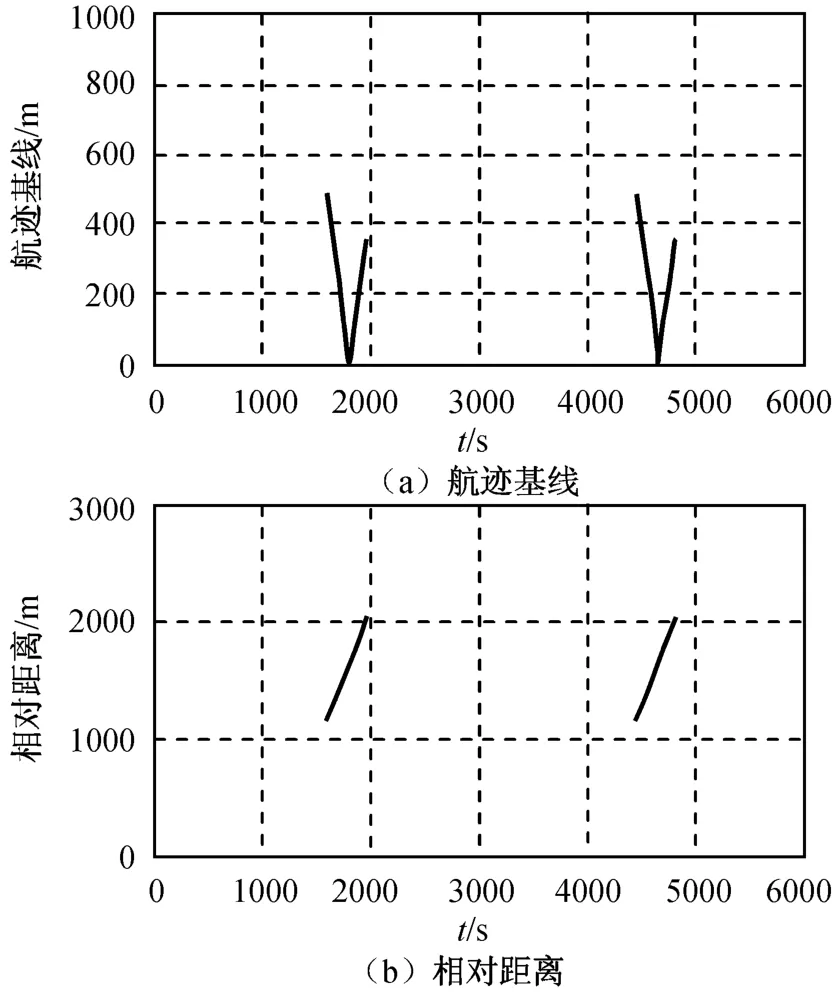
图15 构型2航迹基线范围和两星的相对距离Fig.15 Flying direction rang and two satellites'relative distanceof shape 2

5 结束语

本文用e/i矢量方法设计InSAR编队飞行的构型,可获得从编队几何构型到相对轨道参数的直接关系。用该法在InSAR任务基线与相对距离要求的约束条件下,先设计几何构型参数,而后转为卫星的轨道参数。仿真结果表明：用两种轨道构型,通过三星编队或两星编队(任务过程中通过构型重构实现两种编队)就能基本实现对南纬80°～北纬80°间地区的高程测量。

[1]郗晓宁,王 威.近地航天器轨道基础[M].长沙：国防科技大学出版社.2003.

[2]曾国强,张育林.编队飞行队形设计一般化方法[J].中国空间科学技术,2003,23(2)：21-25.

[3]章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社,1998.

[4]KAZEMINEJAD A A,GILL M.Spaceborne autonomous and ground based relative orbit control for the TerraSAR-X/Tandem-X formation[C]//20th International Symposium on Space Flight Dynamics.Annapolis：[s.n.],2007.

[5]GILL E,D'AMICO S,MONTENBRUCK O.Autonomous formation flying for the PRISMA mission[J].Journal of Spacecraft and Rockets,2007,44(3)：671-681.