偏心有限长大间隙环流的动特性研究

孙启国

(北方工业大学 机电工程学院，北京 100144)

转子动力学特性的研究一直是力学学科的研究热点之一［1，2]。Antunes 等［3，4]基于整体流动模型和 Hirs壁面摩擦系数方程，用解析方法研究了大间隙环流中偏心转子的静特性和动特性。作者基于整体流动模型和更为合理的Moody壁面摩擦系数方程，建立的大间隙环流中转子运动的力学模型，采用数值方法分析了大间隙环流中同心和偏心转子的静特性和动特性［5－7]。然而，以上研究均做了“无限长”大间隙环流的假设，即忽略了沿轴向变量变化的影响。这种假设仅适合于无轴向流动的大间隙环流。因此，后来作者计入了大间隙环流轴向压差等因素的影响，研究了同心有限长大间隙环流的动特性系数［8]。本文基于作者建立的大间隙环流中转子运动的力学模型，用摄动法推导了有限长偏心大间隙环流流场非线性控制方程的零阶摄动方程，该方程是一个非常复杂的三维偏微分方程组，其求解难度较大。本文提出了一种简化方法，该方法基于同心有限长大间隙环流的动特性系数［8]来计算三维偏心有限长大间隙环流的动特性系数。最后应用该方法对偏心有限长大间隙环流的动特性进行了分析。

1 理论分析

基于紊流整体流动模型和Moody壁面摩擦系数方程，作者建立了大间隙环流中转子运动的力学模型，从而得到大间隙环流流场3D非线性微分方程组［5]:

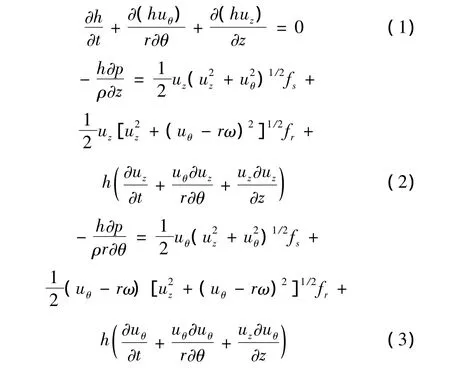
式中:θ和z是周向和轴向坐标;r是转子半径;ω是转子转速;ρ是流体密度;μ是流体动力粘度;p是流体压力;u是流体速度;h是流体膜局部厚度;t是时间;下标θ，z，r和s表示周向、轴向、转子和静子变量;fr和fs是转子和静子Moody壁面摩擦系数，

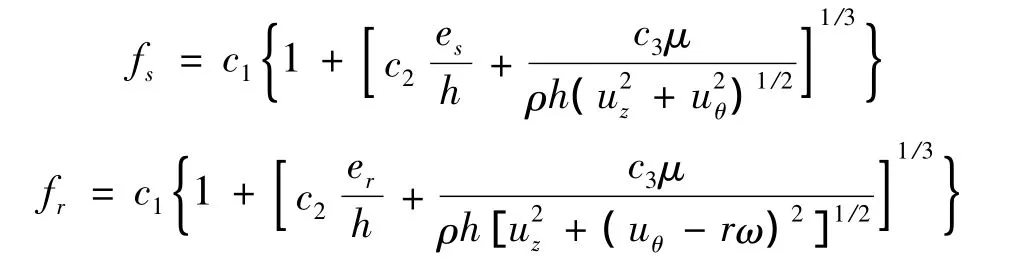
式中:c1，c2和 c3是 Moody实验常数，c1=0.001 375，c2=1×104，c3=5×105;e是壁面粗糙度。

图1为有限长大间隙环流中偏心涡动转子的结构和运动示意图，其中O1为静子中心，O为转子轴心，O2为转子扰动中心，r0为转子扰动半径，动态时O绕O2做小扰动。

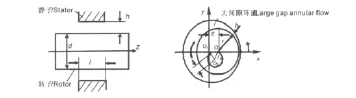
图1 有限长大间隙环流中偏心涡动转子Fig.1 Eccentric whirling rotor in a finite-length large gap annular flow

令ε*为转子轴心O在扰动中心O2附近摄动的摄动变量，将h=h0+ε*h1，代入式(1)～式(3)中，得到零阶摄动方程:

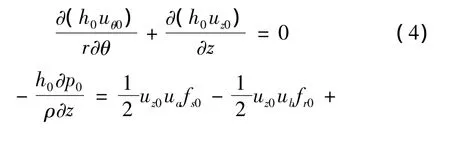
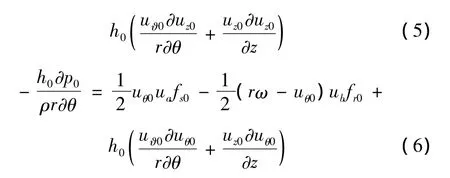
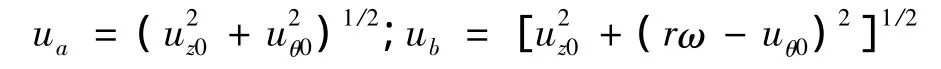
式中:z和θ是方向坐标;下标“z”和“θ”表示z和θ方向变量;该偏微分方程组出现了周向偏导数项和，给求解带来了一定困难，对于复杂的一阶摄动方程更是难以求解。对于同心有限长大间隙环流，其零阶摄动方程经式(4)－(6)可简化为常微分方程组，求解零阶摄动方程组和一阶摄动方程组，可以求得同心有限长大间隙环流的动特性系数，请参见文［8] 。

针对以上方程组求解的困难，本文提出了一种简化的数值计算方法求解偏心有限长大间隙环流的动特性系数，其基本思路为:设在x方向扰动位移为x，流体激振力可用下式表示:

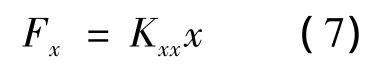
将大间隙环流圆周平分N份，如图2所示，流体激振力可用N段合力表示:

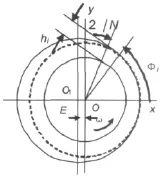
图2 有限长偏心大间隙环流转变为N个间隙为hi的有限长同心大间隙环流Fig.2 N finite-length concentric large gap annular flows that the gap equals hi got from a eccentric one

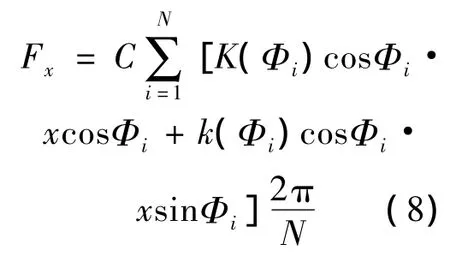
式中:C是待定常数，K(Φi)和k(Φi)为Φi位置上同心大间隙环流(同心大环流间隙为hi)的主刚度和耦合刚度。当N→∞时，

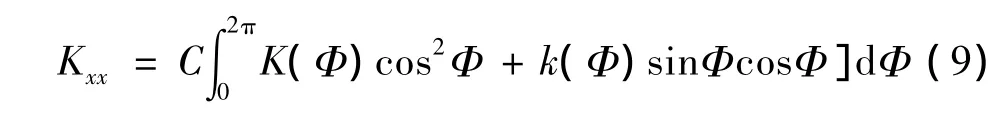
在同心时K(Φi)和k(Φi)不随Φi变化，其值等于Kxx和 Kxy，代入式(9)得 C=1/π，所以，

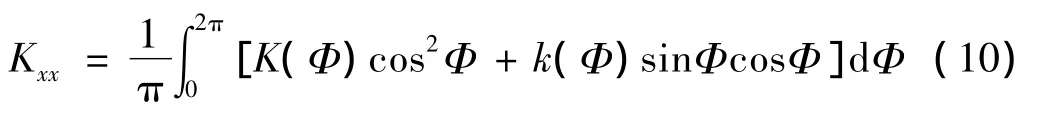
同理，得到:

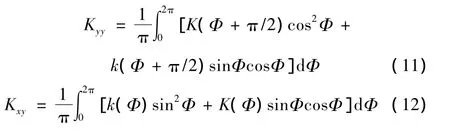
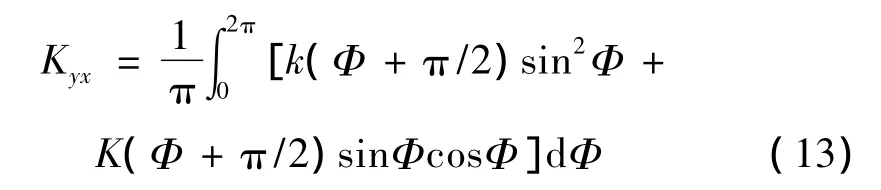
采用同样的方法，得到另外八个系数:

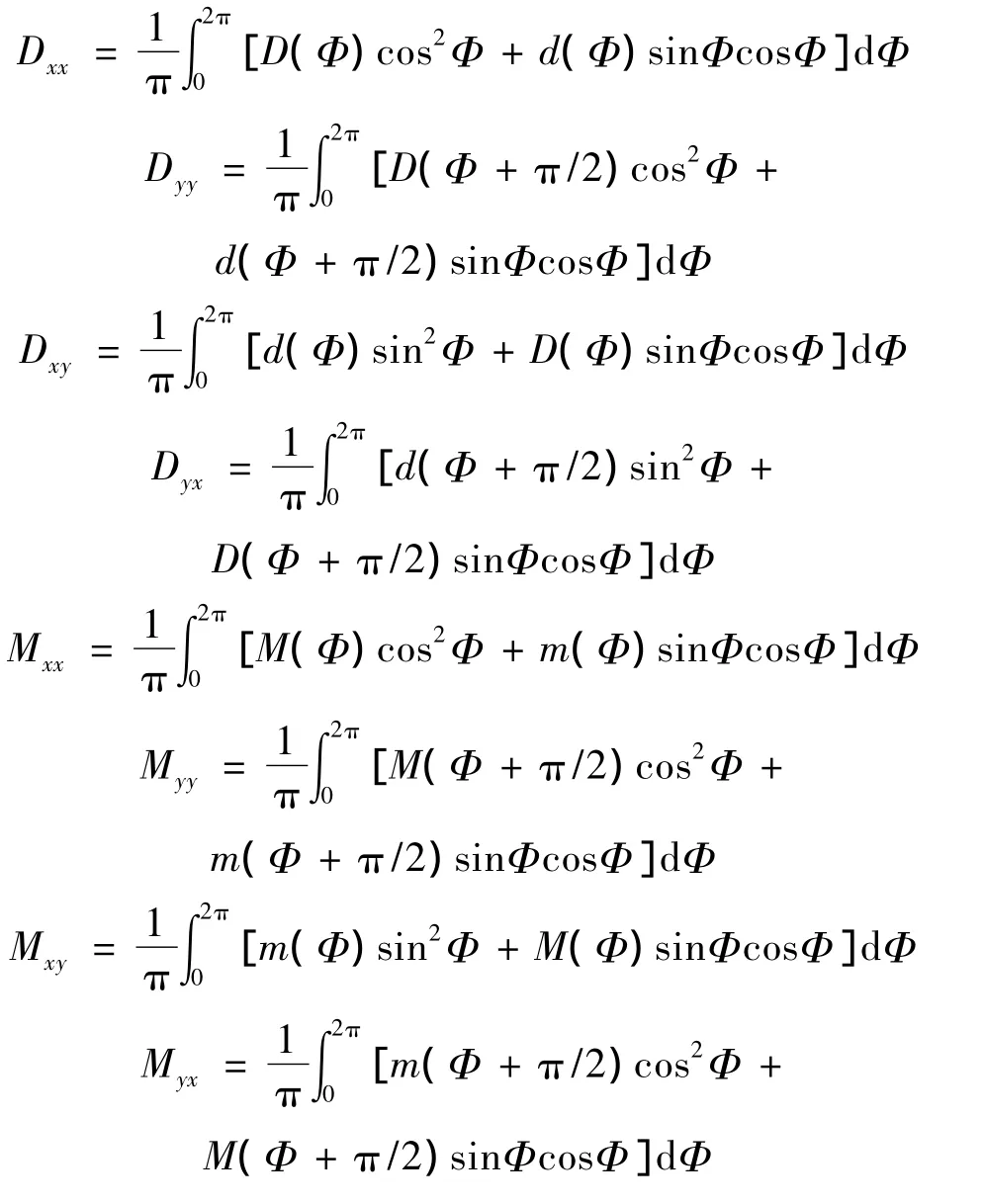
2 数值计算

2.1 与已有结果的比较

基于以上基本思路，采用采用Simpson数值积分方法计算了偏心有限长环压密封动特性系数并与Kanki［9]的实验结果和 Andres［10]的数值结果进行了比较，如图3所示。其主要计算参数为:er/(2h0)=es/(2h0)=0.0，l=D=0.2 m，ΔP=9.8 × 105Pa，C/r=0.005，ω=2 000 r/min。由图3可见本文的计算结果与Andres的数值计算结果在多数计算点上吻合较好。例如当偏心率为0.5时，刚度系数 Kxx，Kyy，Kxy，Kyx的相对误差分别为42%，27%，16%，7%;阻尼系数 Dxx，Dyy，Dxy，Dyx的相对误差分别为 6%，3.7%，9.6%，0%;惯性系数 Mxx，Myy，Mxy，Myx的相对误差分别为2.6%，0.3%，1.4%，8.7%与 Kanki的实验结果在许多测点上也有较好的一致性。例如当偏心率为0.45 时，刚度系数 Kxx，Kyy，Kxy，Kyx的相对误差分别为73%，12%，6.7%，24.9%;阻尼系数 Dxx，Dyy，Dxy，Dyx的相对误差分别为28%，14%，18%，16%;惯性系数Mxx，Myy的相对误差分别为33%，36%。

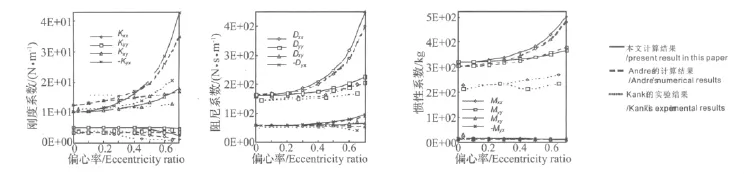
图3 本文计算结果与已有数值计算结果和实验结果的比较Fig.3 Present results comparing with the existing numerical and experimental results

2.2 实例分析

本文以某浸在水中的离心泵转子作为实例研究对象，分析偏心有限长大间隙环流的动特性。主要计算数据为:流体密度 ρ=1.0×103kg·m－3，转子半径r=0.1 m，环流间隙 h0=1.01 ×10－2m，入口损失系数ξ=0.1，转速 ω =6.0 ×103r/min，转子表面相对粗糙度er/(2h0)=1.0 × 10－3，静子表面相对粗糙度es/(2h0)=1.0×10－3，流体粘度 μ =1.3 ×10－3N·s/m2，入口压力 pi=3.0 ×106Pa，出口压力 p0=0.0 Pa，环流长度l=5.8 ×10－2m，进口相对旋转速度 uθi/(rω)=0.2。

计算中先采用文［8] 的计算方法，求得同心有限长大间隙环流的动特性系数，然后采用上述简化的数值计算方法求得偏心有限长大间隙环流的动特性系数。

图4给出了一组不同偏心率下偏心有限长大间隙环流动特性系数的变化曲线。可见偏心大间隙和同心大间隙环流的动特性系数［8]有许多相同与不同点，偏心大间隙环流动特性系数与静偏心有关，系数矩阵的主项不再相等，耦合项也不再反向对称，特性系数主项随着偏心率的增加而呈不同程度的指数增加。例如在偏心率ε从0.0变化到0.9时主刚度由－6.95×104N/m增加到1.93×106N/m，主阻尼项和主质量项也分别增加了约100%和300%。说明偏心有限长大间隙环流动特性系数在大偏心下会增大。

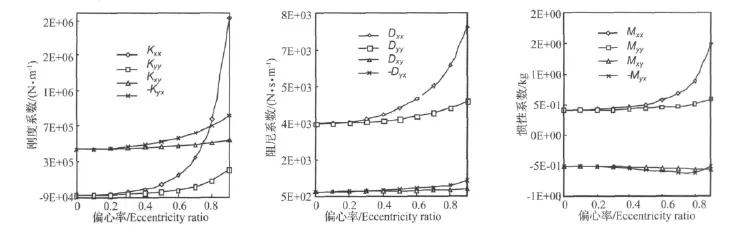
图4 不同偏心率下有限长偏心大间隙环流的动特性系数Fig.4 Dynamic coefficients of a finite-length large gap annular flow under different eccentricity ratio

3 结论

(1)本文提出了基于同心有限长大间隙环流的动特性系数计算偏心大间隙环流的动特性系数的数值计算方法。该方法具有简单方便等优点。本文的计算结果与已有数值计算结果比较表明，在多数计算点上两者吻合较好;与已有实验结果比较表明，在许多测点上两者也有较好的一致性。

(2)有限长大间隙环流动特性系数不具备主项相等，耦合项大小相等、符号相反的特点，特性系数主项随着偏心率的增加而呈不同程度的指数增加。在大偏心情况下有限长大间隙环流中转子动特性系数会增大。

［1] 张文斌，周晓军，杨先勇，等.基于谐波窗方法的转子轴心轨迹提纯［J] .振动与冲击，2009，28(8):74－77.

［2] 赵 广，刘占生，叶建槐，等.转子－不对中花键联轴器系统动力学特性研究［J] .振动与冲击，2009，28(3):78－82.

［3] Antunes J，Axisa F，Grunenwald T.Dynamics of rotors immersed in eccentric annular flow.Part 1:theory［J] .Journal of Fluid and Structures，1996，10:893 －918.

［4] Grunenwald T，Axisa F，Bennett G，et al.Dynamics of rotors immersed in eccentric annular flow.Part 2:experiments［J] .Journal of Fluid and Structures，1996，10:919 －944.

［5] 孙启国，方海容.大间隙环流的三维动力学模型［J] .润滑与密封，2004，165(2):7－9.

［6] 孙启国，姜培林，虞 烈.大间隙环流中壁面摩擦及偏心转子静特性研究［J] .摩擦学学报，1999，19(3):261－265.

［7] 孙启国，虞 烈.粗糙度对大间隙环流中偏心转子动特性系数的影响［J] .摩擦学学报，2000，20(5):365－369.

［8] 孙启国，虞 烈.大间隙环流中同心转子动特性系数研究［J] .摩擦学学报，2001，21(6):472－477.

［9] Kanki H，Kawakami T.Experimental study on the dynamic characteristics of pump annular seals［A] .Proc of the Institution of Mechanical Engineers［C] ，1984，159－166.

［10] Andres L S.Analysis of variable fluid properties:turbulent annular seals ［J] .ASME J of Tribology，1991，113:694－702.