大跨径桥梁结构概率地震需求分析中地面运动强度参数的优化选择

陈 亮， 李建中

(1.合肥工业大学 土木与水利工程学院，合肥 230009;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

在地震环境中，与结构性能和需求相关的大量不确定因素决定了确定性的方法并不适用于结构抗震。因此，采用基于性能的地震工程学的全概率理论(Performance-base earthquake engineering，PBEE)和抗震设计理论(Performance-base seismic design，PBSD)已成为国际地震工程和结构抗震领域的研究热点和未来发展方向。其中，对于结构地震需求的概率预计主要采用概率地震需求分析来获得，并建立相应的概率地震需求模型［1－3]。目前，在结构抗震设计、分析以及 PBEE和PBSD中，对于结构地震需求的预计大部分是通过动力时程分析方法获得，这是目前结构地震反应分析方法中最精确的一种，它需要选择一系列与场地地震危险性相符合的地震波作为输入地面运动，并将地面运动的强度进行量化以反映特定场地的地震危险性，在PBEE中采用地面运动强度参数(Intensity Measure，IM)来表征，IM为一个服从对数正态分布的随机变量。IM的选择对于结构地震需求的概率预计至关重要，一个好的IM能将地面运动强度与结构地震反应水平有效地联系起来，精确、高效地预计结构地震需求［1，4－6]。

国内外关于IM的相关研究主要集中于建筑结构，对于桥梁结构的研究很少。建筑结构和桥梁结构在构造以及动力特性方面的差异较大，特别是对诸如斜拉桥、悬索桥之类的大跨径桥梁，在纵、横桥向质量参与系数贡献显著的模态较多，可能会出现在某一桥向有多阶模态的质量参与系数贡献比较显著，但很难找到某一阶模态的质量参与系数占主导地位，而且竖向地震作用还会影响到主塔等关键构件的纵、横桥向地震响应。因此，高模态效应对大跨径桥梁结构地震反应的影响比其它桥梁结构更加显著，其动力特性的复杂性和特殊性决定了IM的优化选择对于大跨径桥梁结构地震需求预计的影响也更为复杂和重要。

相关研究表明:在桥梁抗震分析和设计中，一般采用结构基本周期处的弹性谱加速度或PGA(峰值地面运动加速度)作为IM，且谱加速度要优于PGA，但这些研究基本上是针对梁桥结构［1，2，7－9]。对于不同的桥梁结构，各种IM的适用性和正确性存在着较大差异，应该从地震工程学和结构抗震两个方面加以分析。因此，本文针对一座高速公路双塔斜拉桥，采用非线性动力时程分析方法，根据频谱特性和高模态效应对于结构地震反应的影响程度，主要研究在影响显著的反应谱区段内选择合理的谱加速度以及PGA作为IM，进行概率地震需求分析，以期更加精确、高效地预计在特定地震危险性水平下的结构地震需求。

1 工程概况与计算模型

本文以一座高速公路双塔斜拉桥为例(以下简称算例斜拉桥)，同时在主桥两侧分别建立一联引桥(连续梁桥)，考虑主桥与引桥的共同作用。主桥为双塔双索面钢箱梁斜拉桥方案，采用的跨径布置为64.5+150.5+436+150.5+64.5 m，全桥总体布置见图 1。主梁为单箱多室流线型扁平钢箱梁，中心线处内轮廓梁高3m，钢箱梁全宽35 m(含两端风嘴)，一端风嘴宽2.23 m。主塔采用钻石型混凝土塔，设置一道横梁。索塔全高150.2 m，桥面以上高度为110.9 m，为变截面箱型截面。塔、墩基础均采用群桩基础，主塔的群桩基础按照摩擦桩设计，桥墩的群桩基础采用钻孔灌注桩。

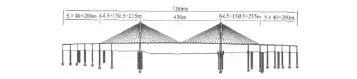
图1 算例斜拉桥立面布置图Fig.1 Elevation of the selected cable-stayed bridge(unit:m)

图2 算例斜拉桥动力分析模型Fig.2 Model of dynamic analysis of the selected cable-stayed bridge

根据桥梁结构总体布置并考虑相邻联的影响，建立了算例斜拉桥结构动力特性和地震反应分析的三维有限元模型(图2)，其弹性及非线性有限元模型均采用通用有限元软件SAP2000建立。主桥除辅助墩、过渡墩及主塔下部的地质条件不同外，上部结构对称。采用空间结构有限单元方法建立计算模型，其中主塔、主梁、桥墩均采用空间梁单元模拟，考虑结构恒载几何刚度的影响;过渡墩、辅助墩及主塔中横梁与主梁纵向均考虑采用摩擦支座连接，对滑动摩擦支座近似采用理想弹塑性连接单元进行模拟;在两个主塔中横梁与主梁连接处，各设置四个纵向粘滞阻尼器;斜拉索采用空间桁架单元，采用Ernst公式修正拉索弹性模量，从而考虑拉索的垂度效应，拉索与主梁及主塔均采用刚体限制连接;在承台质心采用集中质量模拟承台的作用。主塔基础冲刷线以上的桩基采用空间梁单元模拟，冲刷线以下的部分每根单桩采用6×6耦合弹簧来模拟桩土相互作用，其余各墩基础均在承台底采用6×6耦合弹簧来模拟群桩桩土相互作用;各处支座根据其约束特性采用相应的主从约束来模拟。

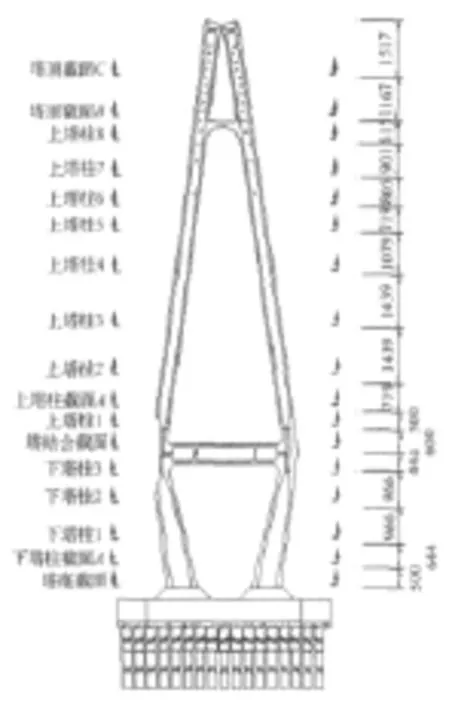
图3 主塔关键位置示意图Fig.3 Key sections of the main towers(unit:cm)

本文主要选取内力响应的关键位置为:上塔柱截面1、下塔柱截面3、塔底截面、承台底截面以及阻尼力。位移响应的关键位置为:塔顶纵桥向位移、主梁梁端纵桥向位移、主梁中点竖向位移、过渡墩和辅助墩的支座纵桥向位移以及阻尼器行程，具体见图3。

2 算例斜拉桥的动力特性

分析和认识桥梁的动力特性是进行抗震性能分析的基础，采用前述的计算模型，对主桥的动力模型进行动力特性分析，并将算例斜拉桥在纵、横桥向和竖向质量参与系数贡献显著的模态列出，具体见表1～表3。其中，仅列出质量参与系数大于0.05的模态，质量参与系数较为显著的几阶模态采用粗斜体。

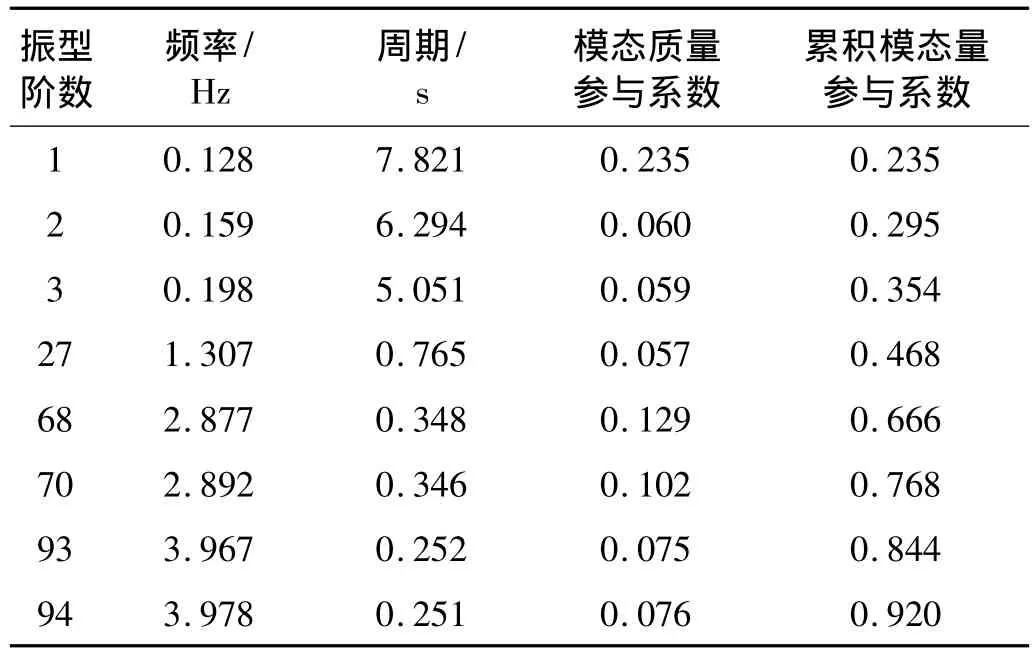
表1 纵桥向质量参与系数贡献显著的模态Tab.1 Vibrational modes of significant modal mass participation in the longitudinal direction of the selected cable-stayed bridge

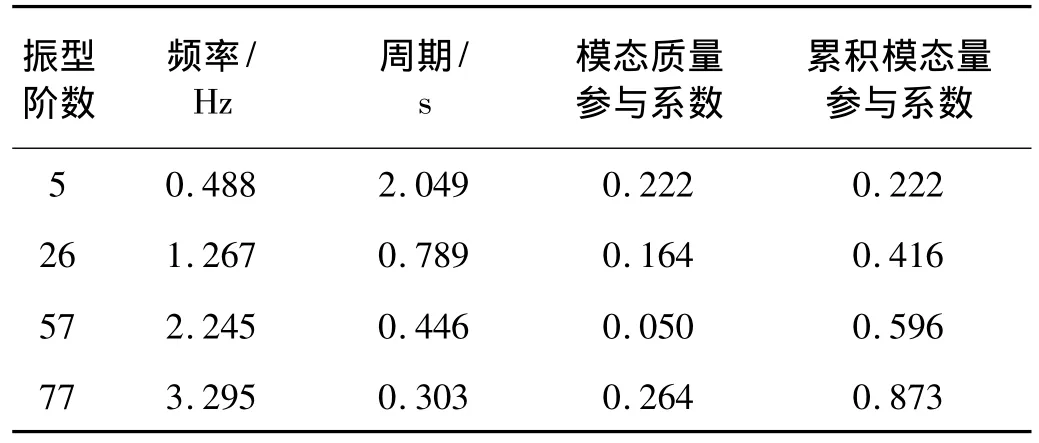
表2 横桥向质量参与系数贡献显著的模态Tab.2 Vibrational modes of significant modal mass participation in the transverse direction of the selected cable-stayed bridge

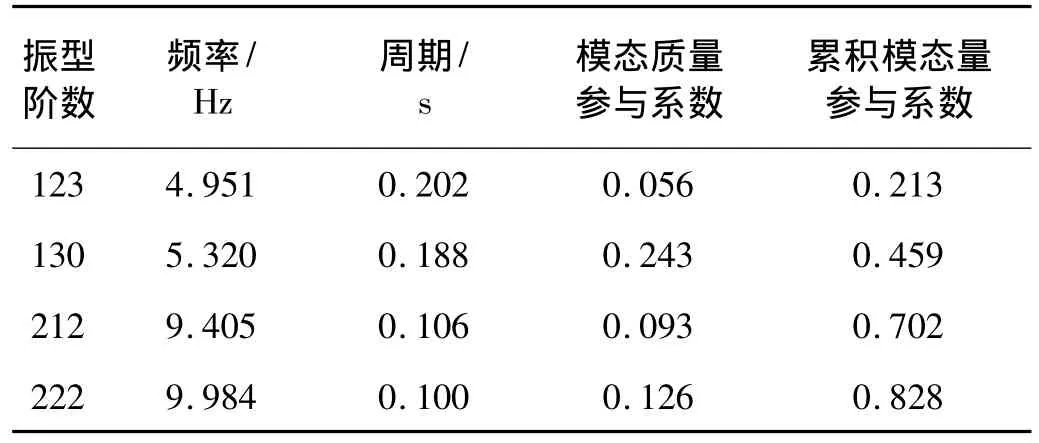
表3 竖向质量参与系数贡献显著的模态Tab.3 Vibrational modes of significant modal mass participation in the vertical direction of the selected cable-stayed bridge

分析表1～表3可知，在算例斜拉桥的纵、横桥向和竖向，质量参与系数比较显著的模态较多，即使最大系数值也不超过0.3，且系数在0.05左右的较多。以纵桥向为例，第一阶模态质量参与系数最大为0.235，而质量参与系数在0.1和0.2之间的有两阶，在0.05和0.1之间的有五阶，而这八阶模态的累积质量参与系数只有0.793，且周期也有明显不同，从0.251 s变化到7.821 s，说明大跨径桥梁结构具有非常显著的高模态效应。在纵桥向，质量参与系数贡献显著的模态周期主要集中在两个范围内，即0.251 s≤T≤0.765 s和5.051≤T≤7.821 s，简称区段 1 和2，在这两个区段内各阶模态的累积质量参与系数分别达到0.452和0.354，且其中至少有一阶以上的模态质量参与系数较大。

3 地震波库(Bin)的选择

根据地震研究所提供的《大桥工程场地地震安全性评价》［10]可得桥位处50年10%超越概率的水平和竖向地震动设计反应谱(3%阻尼比)，以及PGA、周期T1=7.82 s和T2=0.35 s处的弹性谱加速度(3%阻尼比)即 Sa(T1=7.82 s)和 Sa(T2=0.35 s)的50 年10%超越概率水平分别为 0.187 g、0.067 g 和 0.550 g。在进行非线性动力时程分析时地面运动输入采用“纵向+竖向”的方式。

本文选择一个实际地震波库(Bin)作为输入地面运动，共10条地震波，所选地震波的具体资料见表4。在不同工况的纵桥向计算中，采用的竖向地面运动相同，可以更加清晰地分析纵向地面运动强度参数的选择对于斜拉桥纵向地震需求的影响。

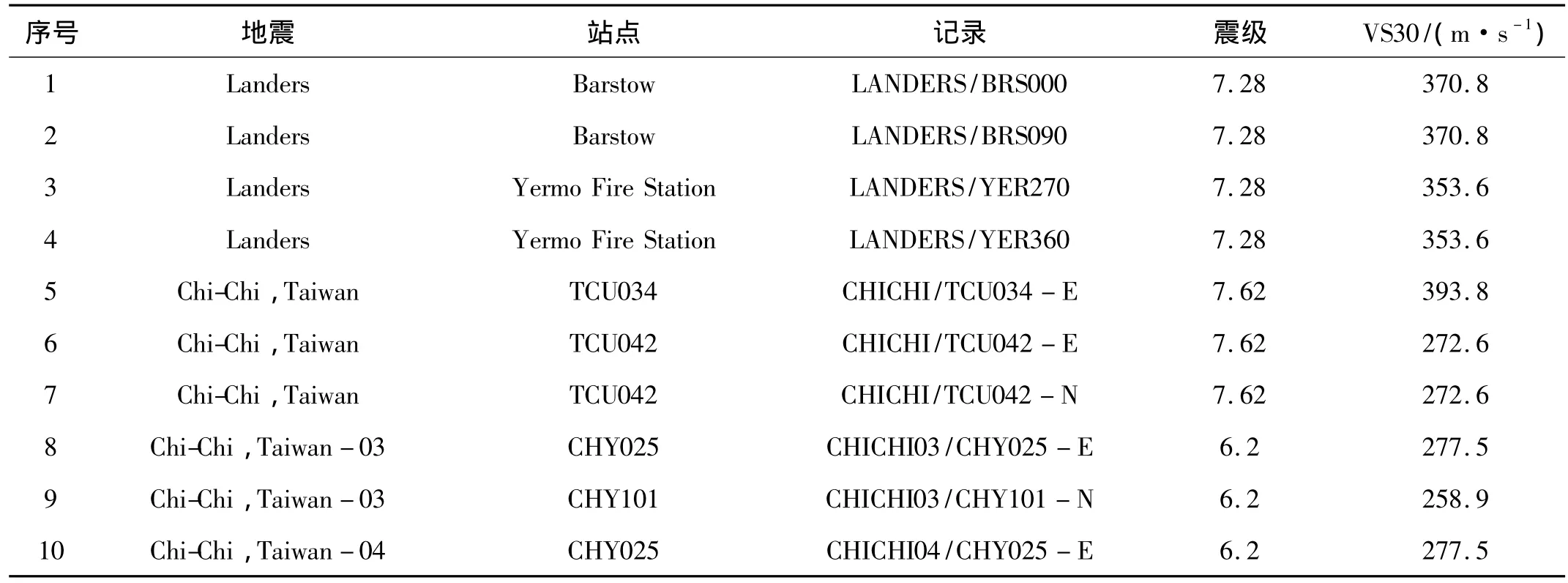
表4 所选实际地震波资料Tab.4 Selected earthquake ground motions

分析图4可知，将Bin中所有地震波的PGA、Sa(T1=7.82 s)和 Sa(T2=0.35 s)分别调整到 50 年 10%超越概率水平后，工况一和工况三的几何平均值谱匹配较好，两条反应谱曲线差异很小，且离散度曲线也相当接近。在区段1内，工况二的几何平均值谱与工况一和工况三的几何平均值谱匹配较好，而离散度曲线基本上是工况二大于工况一和工况三。在区段2内，工况二的几何平均值谱明显大于工况一和工况三，但离散度曲线明显小于工况一和工况三。

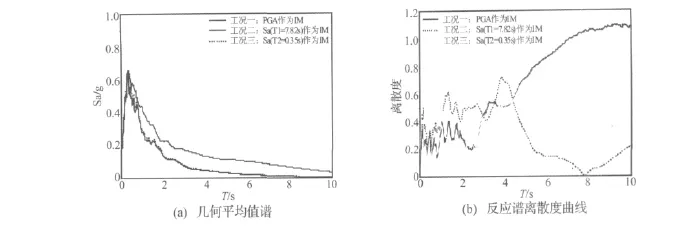
图4 当所选地震波的PGA、Sa(T1)和Sa(T2)分别调整到50年10%超越概率水平时的几何平均值谱(对数坐标系)和反应谱离散度曲线(常数坐标系)Fig.4.(a)Geometric means(on a log scale)and(b)dispersion(on an arithmetic scale)of acceleration response sepctra of selected earthquake ground motions at the level of 10% －in－50－years.

4 纵桥向和竖向计算结果分析

本文主要研究IM的选择对于斜拉桥结构概率地震需求的影响，分析表1～表3可知，在算例斜拉桥纵、横桥向和竖向的动力特性较为相似，均为多阶模态的质量参与系数贡献显著，其中几阶贡献较大，由于非线性支座和阻尼器主要设置在纵桥向，故计算分析主要针对纵桥向。算例斜拉桥在纵桥向为对称结构，因此只选择了半幅桥梁的计算结果，共分为以下三个工况:工况一，采用PGA作为IM;工况二，采用Sa(T1)作为IM;工况三，采用Sa(T2)作为IM。

在工况一和工况三中，将所选地震波的PGA和Sa(T2=0.35 s)分别调整到50年10%超越概率水平即0.187 g和0.550 g;在工况二中，将所选地震波的 Sa(T1=7.82 s)调整到50年10%超越概率水平即0.067 g，这种一次性将IM调整到一定水平，可以减小在计算结果中引入的偏差。在三个工况中，将调幅后的地震波分别作为输入地面运动，对算例斜拉桥进行非线性动力时程分析，所得结果及相关分析如下。在所有的统计分析中，采用几何平均值作为EDP的最佳估计值，离散度采用计算数据自然对数的标准差来衡量［4]。

4.1 位移概率需求分析

从表5分析可知，对于主梁中点最大竖向位移，三个工况的计算结果基本一致，这主要是因为纵向输入地面运动对于竖向位移需求的影响很小，且三个工况的竖向输入地面运动相同，故纵桥向输入地面运动的IM选择和反应谱对于竖向位移影响甚微。

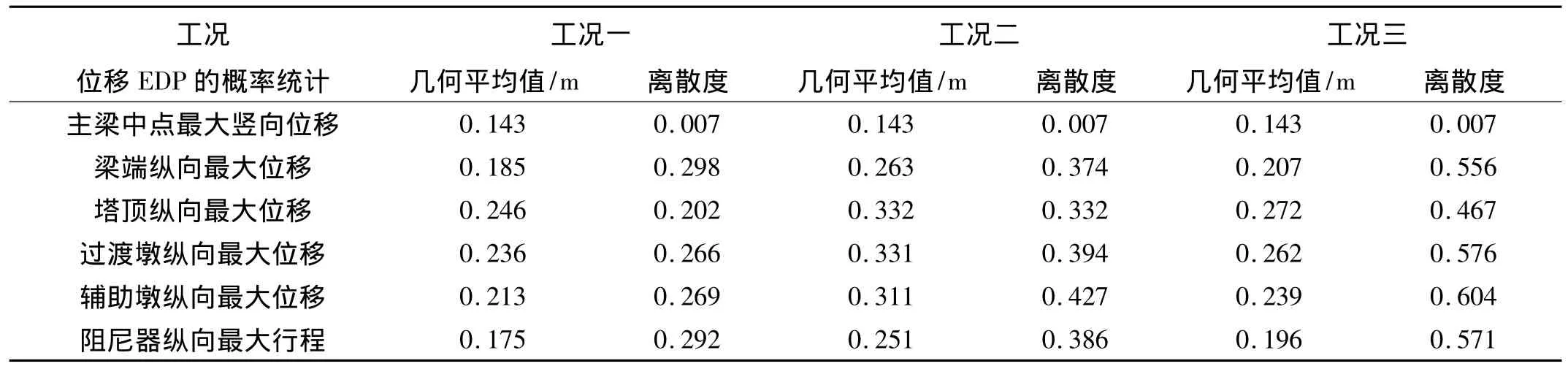
表5 不同工况计算所得各构件最大位移的统计分析Tab.5 Statistical analysis of max displacements in three cases for scaled records

分析斜拉桥重要构件纵向最大位移可知，对于纵向位移需求的概率预计(几何平均值)，三个工况的计算结果具有一定差异。其中，工况二的计算结果明显大于其它两个工况，但工况一和工况三的计算结果较为接近。分析图4(a)可知，这主要是因为将PGA、Sa(T1)和Sa(T2)分别调幅到50年10%超越概率水平后，工况一和工况三的几何平均值谱整体匹配较好，但在反应谱区段2内，工况二的几何平均值谱明显大于其它两个工况，而且随着结构进入非线性后，各阶周期不断延长，区段1和2的范围也随之延长，从而造成在对桥梁结构地震需求影响显著的反应谱区段内，工况二的几何平均值谱均大于工况一和工况三。

对于纵向位移需求的离散度变化趋势基本为:工况一＜工况二＜工况三。分析图4(b)可知，这主要是因为将PGA、Sa(T1)和Sa(T2)分别调幅到50年10%超越概率水平时，在反应谱区段1内，工况二的反应谱离散度明显大于其它两个工况，且工况一最小;在区段2内，工况二的反应谱离散度明显小于其他两个工况。但在区段1内各阶模态的累积质量参与系数(0.452)大于区段2(0.354)，且区段1处于峰值平台段，对于结构地震需求的影响要明显大于区段2，故离散度主要受到区段1内反应谱离散度的影响。

4.2 内力概率需求分析

从表6分析可知，对于各关键截面内力的概率预计，由于轴力主要受到竖向地面运动的影响显著，故纵向地面运动的IM选择和反应谱对其影响甚微。对于剪力和弯矩以及阻尼器力，其规律是工况二的计算结果明显大于其它两个工况，但工况一和工况三的计算结果较为接近。对于各关键截面内力的离散度，则基本上是工况一＜工况二＜工况三。以上规律与位移需求基本一致。其中，计算结果的离散度越小意味着计算结果的精确度越高，或在精确度相同的情况下，所需的地震波数量越少，计算效率越高。

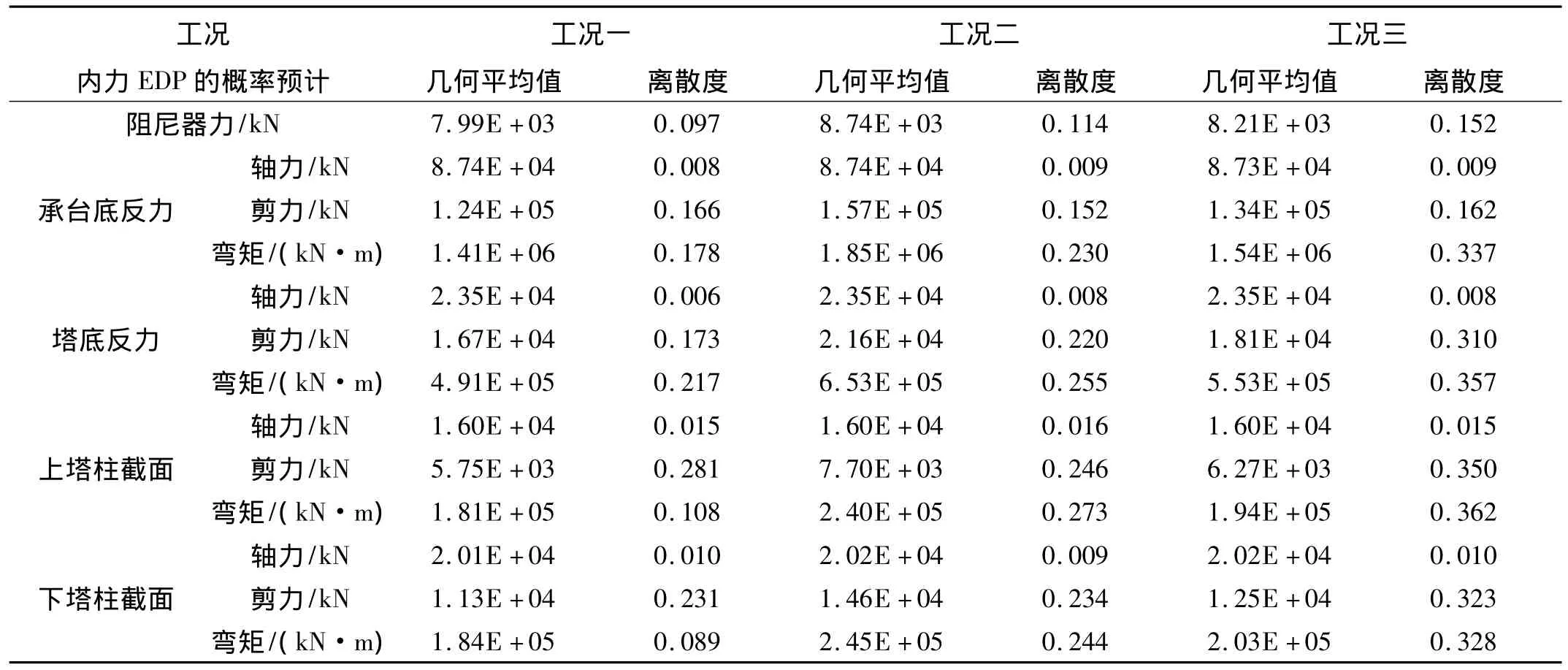
表6 不同工况计算所得各构件最大内力的统计分析Tab.6 Statistical analysis of max forces in three cases for scaled records

综上所述，输入地面运动的反应谱在区段1和2内的谱形及其离散度对结构地震需求的影响显著，以下简称为显著区段。对于不同的IM，将所选地面运动的强度调整到相应水平后，使其反应谱在显著区段内与目标谱匹配较好，则计算结果是基本一致的。由地震波反应谱与结构地震需求之间的密切联系可知，谱加速度比PGA更加适合作为IM，大量文献［1，4]也发现谱加速度作为IM使得计算结果的精确性和计算效率均明显高于PGA。但通过本文的分析可知，对于不同的IM，调幅后在显著区段内所选地震波的反应谱离散度越小，计算结果的精确性和计算效率也越高，采用PGA作为IM一样能够取得很好的效果，可以显著扩大IM的选择范围。

对于大跨径桥梁结构，其基本周期一般较长，甚至超过10s，故谱加速度值通常较小，会产生IM很小但地震反应很大的现象，使得地面运动强度水平与结构地震反应水平之间缺乏对应性。而且，在地震工程学中长周期反应谱尚处于发展阶段，以目前的发展水平，当周期超过10s后，通过计算得到的谱加速度值的正确性已经受到质疑，可能会导致计算结果出现明显偏差。因此，在这种情况下，Sa(T1)已不再适合作为IM，可以采用质量参与系数较大的短周期谱加速度或PGA作为IM。

4.3 偏差分析

在桥梁抗震设计、分析以及PBEE和PBSD中，通常需要将输入地面运动记录的幅值进行调整以获得具有目标IM水平的记录，调幅后的地震波是否可以代表给定IM水平下的地面运动是值得质疑的。如果可以代表，那么调幅不会在所求的结构地震反应中引入偏差，即可获得地震反应的无偏估计;反之，则会引入较大偏差。引入误差与否不但取决于所选的地震波，而且不同IM对其也有较大影响。由于结构地震需求服从对数正态分布［1－4]，故一个非常直观的方法就是选取一组地震波，将其IM调整到给定的水平进行动力分析，将计算所得结构地震反应作为调幅系数的函数，并在对数坐标系下对数据点进行线性回归分析。如果回归直线的斜率为0，则说明调幅并不会在计算结果中引入偏差，即结构地震反应的均值预计并不取决于记录是否经过调幅［11]。从概率统计理论上，当调幅到目标IM水平的记录与未经调幅时IM即具有目标水平的记录(调幅系数为1)所产生的结构地震反应水平相同，则说明由调幅记录所求得的是对结构地震反应的无偏估计，这时记录调幅才是正确可行的［12]。本文选择塔顶最大纵向位移和塔底弯矩分别代表位移需求和内力需求进行偏差分析，其它反应参数的规律与此相同。

分析图5可知，工况一中数据点的回归拟合直线的斜率最小，接近于0，其次是工况三，斜率最大的是工况二，其中，实线代表通过对数据点进行线性回归分析得到的回归拟合直线，虚线代表调幅系数为1时对结构地震反应的均值预计。分析表明对于算例斜拉桥，采用PGA作为IM进行调幅计算所得的结构地震反应引入的偏差最小，采用Sa(T2)次之，采用Sa(T1)引入的偏差最大。

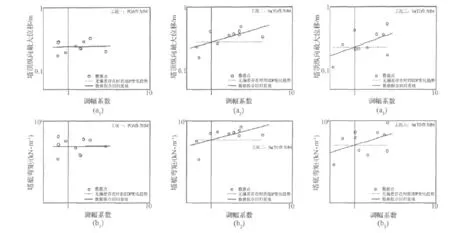
图5 在三个工况中，塔顶纵向最大位移和塔底弯矩作为调幅系数的函数进行线性回归分析所得回归拟合直线(实线)与调幅系数为1时的均值预计(虚线)对比图(对数坐标系)Fig.5(a1)～ (a3)Maximum longitudinal displacement on the top of main towers and(b1)～ (b3)bending moment at the bottom of main towers versus record scale factor for each of the three cases considered，at the level of 10% －in－50－years(on a log scale).Regression fit based on scale factor are shown with solid lines.Dashed horizontal lines corresponding to the mean prediction at a scale factor of on are shown for comparison.

5 结论

在桥梁抗震分析和设计中，动力时程分析是目前最精确的分析方法，需要选择正确的输入地面运动，并采用合理的地面运动强度参数(IM)表征实际的地震危险性水平。针对不同的桥梁结构，各种IM的适用性和正确性存在着显著差异。本文针对大跨径桥梁结构在动力特性方面的复杂性和特殊性，以某座实际的高速公路双塔斜拉桥为例，同时在主桥两侧分别建立了一联引桥(连续梁桥)，考虑主桥与引桥的共同作用。采用通用有限元软件SAP2000为该桥建立弹性和非线性有限元模型，分析其结构动力特性，并讨论不同性质的I M对于大跨径桥梁结构概率地震需求的影响。通过分析，可以得到以下结论:

(1)在累积质量参与系数贡献显著且具有至少一阶以上的模态质量参与系数较大的周期范围内，其反应谱对结构地震需求影响显著。在累积质量参与系数相近的情况下，高频区段反应谱的影响大于低频区段。

(2)当输入地面运动的反应谱在对结构地震需求影响显著的区段内与目标谱匹配较好，且反应谱离散度越小，则计算结果的精确性和计算效率也越高，并可以显著扩大I M的选择范围。

(3)由于大跨径桥梁结构高模态效应显著且基本周期一般较长，故基本周期处的谱加速度已不再适合作为I M，且调幅会在计算结果中引入明显的偏差。

可以采用目标谱匹配的方法［12－14]选择输入地面运动，并采用在对结构地震需求影响显著的区段内质量参与系数较大的短周期谱加速度或PGA作为IM。

［1] Kevin M，Bozidar S.Seismic demands for performance-based design of bridges［R] .Pacific Earthquake Engineering Research Center College of Engineering University of California，Berkeley.PEER Report，2003.

［2] Sashi K.Kunnath.Application of the peer pbee methodology to the I－880 viaduct［R] .Pacific Earthquake Engineering Research Center College of Engineering，University of California，Berkeley.PEER Report，2006.

［3] Bazzuro P.Probabilistic seismic demand analysis［D] .Dept.of Civil and Environmental Engineering，Stanford University，California，1998.

［4 ] Shome N，Cornell C A，Bazzurro P，et al.Earthquakes，records and nonlinear responses［J] .Earthquake Spectral，1998，14(3):469 －500.

［5] 胡聿贤.地震工程学［M] .北京:地震出版社，2006:150－173.

［6] Shome N.Probabilistic seismic demand analysis of non-linear structures［D] .Stanford University，1999.

［7] Padgett JE，Nielson B G，DesRoches R.selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios［J] .Earthquake Engineering And Structural Dynamics，2008，37(5):711 －725.

［8] Nielson B G，Des Roches R.Seismic fragility methodology of highway bridges［C] //Structure Congress，2006:Structural Engineering and Public Safety.

［9] Nielson B G，DesRoches R.Seismic fragility methodology for highway bridges using a component level approach ［J] .Earthquake Engng Struct.Dyn，2007，36:823 －839.

［10] 中国地震局地质研究所.广深沿江高速公路工程场地地震安全性评价［R] .工作报告，2004K02.2004.

［11] Neter J，Kutner M H，Nachtsheim CJ，et al.Applied linear statistical models［M] .McGraw-Hill，Boston，1996，1408.

［12] Baker J W.Vector-valued ground motion intensity measures for probabilistic seismic demand analysis［D] .Stanford University，2005.

［13] Jorge E，Carballo A.Probabilistic seismic demand analysisspectrum matching and design ［D] . Stanford University，2000.

［14] 陈 亮.地面运动特性对典型桥梁结构地震需求的影响研究［D] .上海:同济大学，2009.