密集模态挠性结构振动的自适应逆控制

王 永， 姚太克， 陈 光，2

(1.中国科学技术大学 自动化系，合肥 230027;2.北京航天时代激光导航技术有限责任公司，北京 100143)

空间大型挠性结构的振动控制问题是航天控制领域挑战性课题之一，一般大型挠性航天器具有阻尼小、模态密集等特点［1－3]，所处的外太空环境几乎无空气阻尼，各种内部和外部的干扰很容易激起长时间的低频振动，会造成挠性结构的疲劳破坏，也会影响姿态控制系统、定位系统等的正常工作，需要对振动进行控制。目前，密集模态挠性结构振动控制的研究还不是很充分，控制器设计大都沿用传统振动主动控制中的方案。模态控制和最优控制是常用的控制策略，已经在许多挠性结构振动控制系统中得到验证［4，5]，能很好地解决密集模态挠性结构在相当长一段时间内不发生变化且其模型可以较准确获取的一类问题。但是，空间工作环境无法精确建模和模拟且复杂多变，如航天器经过太阳的阳面和阴面、不同位置受到不同角度的太阳照射等都可能导致其结构参数发生较大的变化，在地面上事先设计好的最优控制器或其他固定参数控制器也许会失灵，甚至可能引起控制系统的失稳，因此，在线自适应控制的研究势在必行［1，6]，包括模型参考自适应控制、自校正控制、变结构控制及基于自适应滤波的自适应逆控制等。

自适应逆控制(Adaptive inverse control)是美国斯坦福大学教授Widrow提出的［7]，其基本思想是利用被控对象传递函数(矩阵)的逆作为串联控制器对系统的动态特性作开环控制，具有形式简单，易于实现，稳定性好等特点，已经在许多领域得到广泛的应用，如Rouse等［8]将自适应逆控制应用于加速器电子束的扰动消除系统之中，李嘉全［9]将其应用于浮筏系统的振动主动控制中，取得了良好的减振效果，但在密集模态挠性结构振动控制中的应用，还未见到文献报道。

本文针对空间大型挠性结构具有模态密集和参数易变的特点，采用多变量自适应逆控制策略进行扰动抑制实验研究。在已构造的二维密集模态挠性板实验系统上，进行自适应建模和自适应逆建模的研究，最后进行扰动控制和变参数扰动控制的实验研究。

1 自适应逆控制基本原理

自适应逆控制是利用被控对象传递函数(矩阵)的逆作为串联控制器对系统的动态特性作开环控制，根据反馈误差信号和自适应算法调整控制器参数，使得控制器和对象的级联在收敛后具有参考模型类似的动态响应，其控制结构如图1所示。同时，自适应逆控制将系统动态特性的控制与对象扰动的控制分开处理而互不影响。对象扰动的消除如图1虚线框所示，对象输入同时激励对象和对象模型(没有噪声和扰动)，对象输出与对象模型输出之差就是对象的噪声和扰动。用该噪声和扰动作为逆对象模型的输入，滤波后的输出反馈到对象输入中，即可消除噪声和扰动。

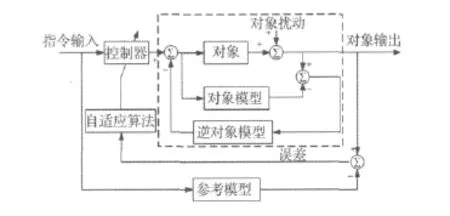
图1 具有扰动消除的模型参考自适应逆控制系统Fig.1 Model-reference adaptive inverse control system

自适应逆控制主要由两部分组成:对象自适应建模与自适应逆建模，分别建立对象模型和控制器。线性系统自适应逆控制的对象模型和控制器一般均采用有限脉冲响应滤波器形式［10，11]，自适应算法采用最小均方算法(LMS)或其改进形式。

2 密集模态挠性板振动控制实验系统

本文针对已建立的二维H型密集模态挠性板振动控制物理实验系统［12]，研究密集模态挠性结构振动的自适应逆控制。图2给出了H型密集模态挠性板的示意图。

表1 H型挠性板的相关参数Tab.1 Parameters of H-like flexible plate

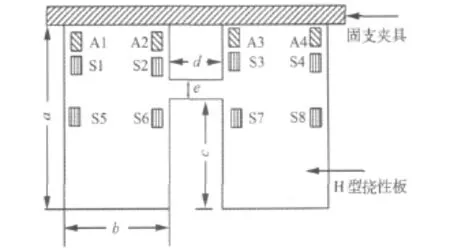
图2 H型挠性板实际的传感器和作动器配置示意图Fig.2 Configurations of sensors and actuators of H-like close model flexible plate

图中A1～A4是作动器，S1～S8为传感器，其中S5～S8仅作观测使用，不参与系统闭环控制，传感器、作动器均为压电陶瓷。挠性板和压电陶瓷尺寸、材料参数见表1和表2。

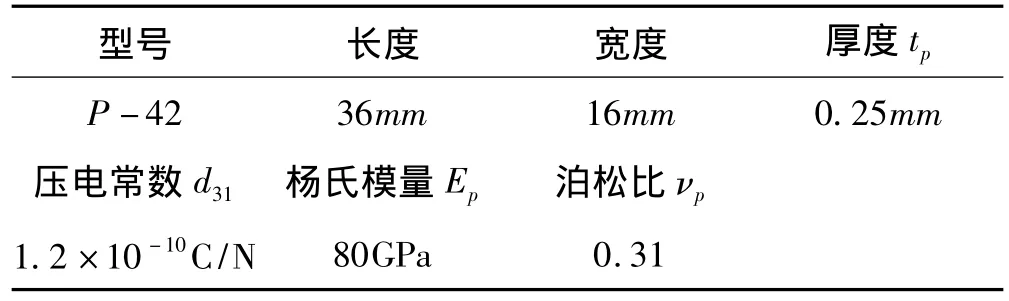
表2 压电陶瓷的相关参数Tab.2 Parameters of piezoelectric ceramics

根据有限元分析和正弦扫描结果，二维H型密集模态挠性板系统前12阶固有频率如表3所示。可以看出，1、2、3、4阶模态为密集模态，它们都具有较小的阻尼。进一步的实验可以得知，5阶以上模态相对而言，模态阻尼较大，并且第5阶模态频率较第4阶大将近一倍，相对而言更难被激发出来，为降低系统复杂度，在此我们仅考虑前4阶模态的振动情况。

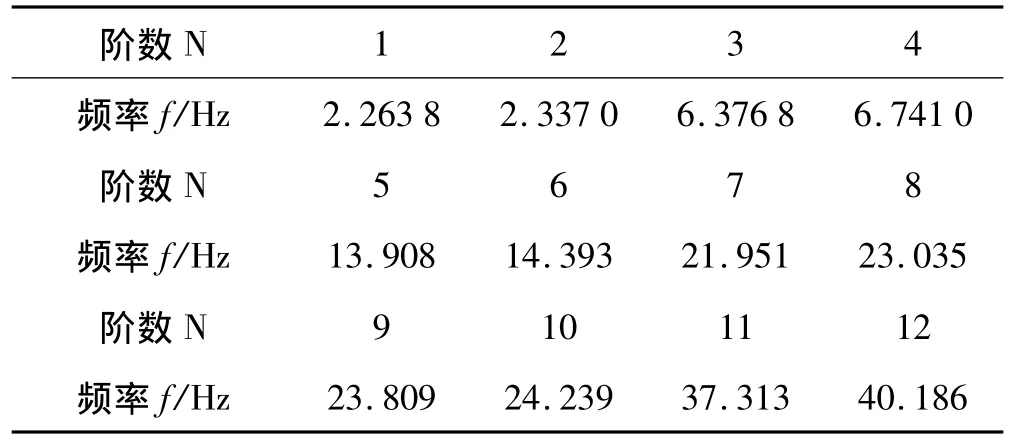
表3 H型挠性板的前12阶固有频率Tab.3 The first 12 models of H-like flexible plate

3 密集模态挠性板的自适应建模和自适应逆建模研究

在密集模态挠性结构的振动控制中，目标是使系统的振动输出为零，故图1中的指令输入为零，从而实际自适应逆控制结构只需扰动抑制部分，如图3所示，图中(z)是自适应扰动消除器。

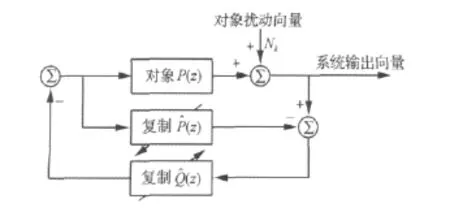
图3 密集模态挠性结构的自适应扰动消除控制结构Fig.3 Controller structure of adaptive disturbance-canceller of close model flexible plate

下面将根据自适应逆控制的一般步骤，建立密集模态挠性板的自适应模型及其逆模型。

3.1 自适应建模

采样对象输入输出数据，自动调节自适应模型参数以产生一个输出，当对象输出与模型输出非常接近的时候，则可认为该自适应脉冲响应就是对象脉冲响应的一个好的表示。但是在任意迭代时刻k，自适应模型和对象P之间总会有差别，该差别称为失配。为了克服因输入信号不充分引起的模型失配，常在输入信号中附加随机抖动信号，使对象输入在所关心的频段内具有均匀谱密度。

H型密集模态挠性板实验系统是一个4输入4输出的MIMO系统，其建模结构如图4。建模信号是4路不相关的白噪声，采样频率为40 Hz，脉冲响应长度均取800，自适应算法是文献［6] 提出的基于相关误差的变步长LMS，该算法具有较快的收敛速度和较好的收敛精度。

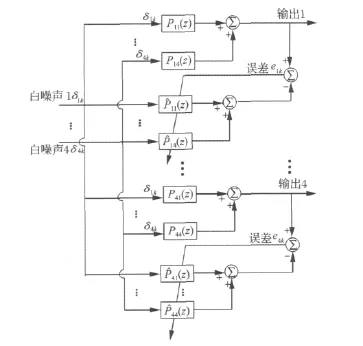
图4 MIMO系统自适应建模结构图Fig.4 Structure of MIMO adaptive modeling

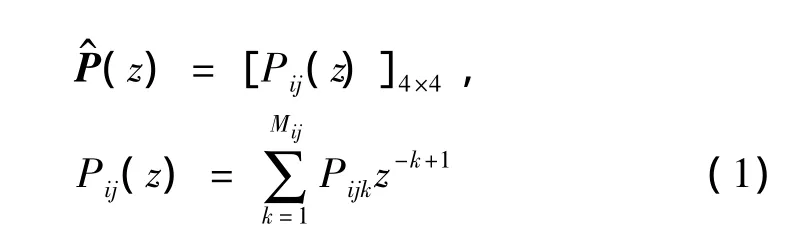
其中，Mij为第i路输出j路输入通道模型的脉冲响应长度，本文均取800。

3.2 自适应逆建模

对于图3所示的扰动消除问题，自适应逆建模就是获取扰动消除器(z)的过程。由于MIMO系统运算的不可交换性，需采用 Filtered－error LMS方法［7，13]，其实现过程如图5所示。先求得对象模型的一个延时逆，然后利用对对象输出进行滤波，从而得到消除器自适应过程所需要的误差，只不过该误差延时了Δ步，于是在自适应过程中对(z)的输入也要延时相同的步数，延时步数一般为自适应滤波器长度的一半。

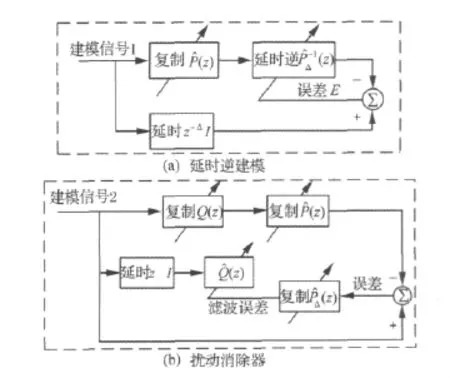
图5 MIMO系统扰动抑制控制器的实现Fig.5 Realization of MIMO disturbance-canceller

4 密集模态挠性板的振动控制实验

4.1 扰动抑制

扰动激振信号采用0～10 Hz的多正弦信号，激振频率与控制频率相同取40 Hz，扰动激振信号重复输入3遍，仅在第2遍时施加控制，图6给出了实际的控制效果，虚线框内代表施加控制后的系统响应。可以看出，没有控制之前，系统输出较大，响应中较大的尖峰值说明系统处于共振状态。施加控制之后，系统输出明显减小，尖峰值也被大大降低。

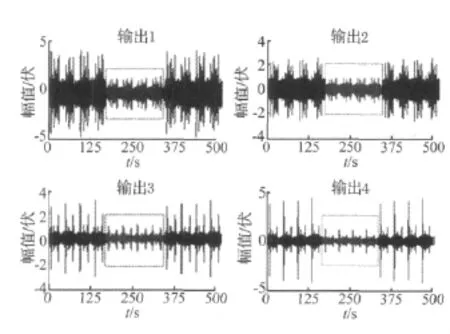
图6 扰动的自适应逆控制Fig.6 Results of adaptive inverse disturbance control

为了便于比较，下面采用文献［5] 中提出的基于频域辨识模型设计的固定参数控制器对系统进行控制。扰动激振信号仍然采用0～10 Hz的多正弦信号，激振和控制频率相同取100 Hz，扰动激振重复三遍，仅在第2遍时施加控制，图7给出了控制效果。虚线框内表示控制后的输出，可以看出，控制之后，系统输出也被抑制在一个较低的水平。

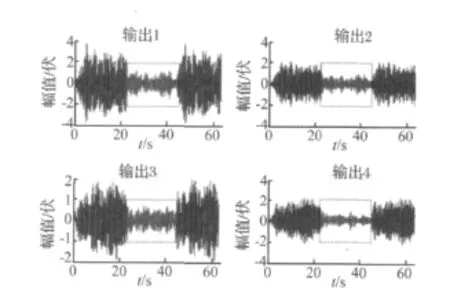
图7 固定参数控制器的扰动消除Fig.7 Results of fixed-parameter disturbance control

为了更直观的观察自适应逆控制的控制效果，以控制前后系统输出均方之比作为评价标准进行定量分析。表4给出了两种方法的控制效果，从表中可以看出，自适应逆控制的效果要好一些。

表4 持续扰动控制前后系统输出均方之比Tab.4The ratios of output mean square with and without control

4.2 对象参数变化时的自适应逆控制

自适应逆控制更大的优势在于其自适应性。下面考虑对象参数变化时，控制器的在线更新问题。采用一段时间内输出均方和作为控制效果的评价指标，当连续几个时间段内输出均方和均无减小的趋势，则认为系统参数发生了显著变化，此时，切断控制器，重新在线建立对象的模型和逆模型，进而实现自适应逆控制。

在本文所建的密集模态挠性结构对象上，粘贴一块薄板以及两个铜块，如图8所示，使对象参数发生变化。

图8 参数发生变化的挠性板Fig.8 Flexible plate with changed parameters

此时仍采用原来的控制器进行控制发现，系统输出会逐渐增大，如图9所示，前面为未加控制的系统输出，后面颜色较深部分为采用原来控制器的控制效果。

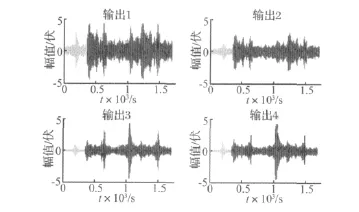
图9 采用原控制器系统输出Fig.9 Results of output with the former controller

切断原来的控制器，开始新一轮的在线辨识，过程和上面相同。自适应过程收敛后，会自动再将所得控制器切换到闭环，针对持续扰动得到了如图10所示的控制效果，其中前面为未加控制的系统输出，后面为自适应逆控制后的效果。可以看出，自适应逆控制可以跟随系统参数的变化，达到很好的控制效果，这是固定参数控制器不能做到的。

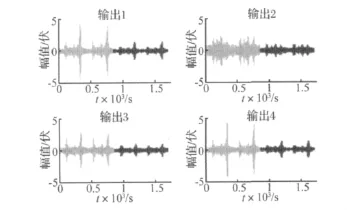
图10 自适应逆控制器收敛时扰动抑制效果Fig.10 Results of output with adaptive inverse controller

5 结论

本文针对已建立的H型二维密集模态挠性板，进行自适应建模和自适应逆建模研究，并实现了对扰动的有效抑制，与固定参数控制器的控制效果进行比较，结果表明自适应逆控制对密集模态挠性结构振动抑制的有效性;改变挠性板结构参数，控制系统重新进行在线辨识和控制器参数自适应调整，实现新状态下振动的有效控制，验证了自适应逆控制对密集模态挠性结构振动的控制具有强大的自适应优势。

［1] 沈佐宁.挠性结构的智能控制方法研究［D] .南京:南京理工大学，2009.

［2] 张国琪，丁建钊，吴宏鑫.基于特征模型的柔性机械臂自适应补偿控制［J] .中南大学学报，2007，35(l):547－552.

［3] 邱志成.航天器挠性板系统的模态分析和模型降阶［J] .航天控制，2006，24(3):89－96.

［4] 魏燕定，陈定中，程耀东.压电悬臂梁振动的模态控制［J] .浙江大学学报(工学版)，2004，38(9):1180－1184.

［5] 陈 光，王 永.密集模态挠性结构模型多变量频域辨识和控制［J] .实验力学，2008，23(2):47－54.

［6] 陈 光.密集模态挠性结构的多变量实验辨识及自适应逆控制［D] .合肥:中国科学技术大学，2006.

［7] Widrow B，Walach E，著，刘树棠，韩崇昭，译.自适应逆控制［M] .西安:西安交通大学出版社，2000.

［8] Rouse F，Castillo S，Allison S，et al.Database driven fast feedback system for the Stanford linear collider［J] .Physics Research，1991，316(2):343－350.

［9] 李嘉全.浮筏系统的振动主动控制研究［D] .合肥:中国科学技术大学，2008.

［10] Widrow B，Stearns S D.Adaptive signal processing［M] .Prentice － Hall，1985.

［11] Haykin S.Adaptive filter theory［M] .Publishing House of Electronics Industry，2003.

［12] 陈 光，王 永，万 璞.密集模态挠性结构传感器/作动器的优化配置［J] .实验力学，2006，21(3):1－7.

［13] 张端金，刘 侠.X－滤波和ε－滤波LMS算法性能分析［J] .郑州大学学报(理学版)，2004，36(1):49－52.