斜拉索风雨振非平稳风场特性分析

何旭辉，陈政清，李春光，，方 俊

(1.中南大学 土木工程学院，长沙 410075;2.湖南大学 风工程试验研究中心，长沙 410082)

斜拉桥拉索由于柔度大、质量和阻尼较小，在风雨共同作用下很容易产生剧烈的大幅振动，即所谓风雨振，自从20世纪80年代末在日本被发现后，已在全世界许多斜拉桥上被观测到［1－3]。大幅的拉索振动容易导致拉索及保护系统的疲劳破坏，危及桥梁的运营安全，同时还易引起公众的担心和恐慌，造成不良的社会影响。因此，从其被发现之日起，一直是桥梁管理部门、工程界和学术界关注和研究的热点之一。目前研究拉索风雨振的方法主要有理论研究［4]、风洞试验［5]和现场观测［6，7]等，取得了大量的研究成果，对风雨振有了一定的认识。国内外研究者在抑制拉索风雨振动方面也进行了大量试验研究和有效应用［8－10]。然而，拉索风雨振是非常复杂的固－液－气耦合振动，影响因素多。张琪昌等［11]研究表明结构阻尼系数、水线与拉索之间的粘附系数以及水线单位长度质量是影响拉索风雨振的主要因素，但未提及风场特性影响。风雨振的振动机理还有待进一步的探索和研究。

与数值模拟拉索表面风速和风荷载［12]相比，现场观测被认为是非常直观、有效的研究拉索风雨振的方法。现场观测已表明，风雨振时风速风向以及拉索振动都不可能长时间保持平稳状态［6]，具有明显的非平稳性，仍采用平稳假定和模型可能会造成一定的分析误差［13]。然而目前关于风雨振现场观测信号的研究大多基于平稳假设，即认为风以及拉索响应均为一个平稳的随机过程，采用平稳的方法进行研究，基于非平稳的分析鲜有报道。因此研究风雨振时实测风速、风向和拉索振动响应的非平稳性对探索拉索风雨振振动机理具有一定的工程意义。

非平稳随机过程的主要特点表现为:①各域(时域、频域、幅域)信息都与时间有关;②不是各态历经的。对实测的非平稳信号处理就不宜采用平稳分析方法，需要采用非平稳的方法。本文从非平稳的角度，结合洞庭湖大桥风雨振时实测的典型风资料，基于小波分析提取时变平均风和建立非平稳的风速模型，计算了各重要的风场参数。同时，通过计算小波系数，分析了风雨振时拉索振动加速度响应非平稳特性和导致拉索振动非平稳性的原因。

1 洞庭湖大桥及试验简介

洞庭湖大桥是湖南省岳阳市跨越洞庭湖口的一座特大型桥梁，也是我国第一座三塔双索面混凝土斜拉桥，跨度为130 m+310 m+310 m+130 m，桥宽23.4 m，双向4车道。全桥共222根拉索，索长为28 m～201 m，索的直径为 99 mm ～159 mm，拉索倾角 30°～90°。中塔布有23对索，边塔布有17对索，索间距8 m，呈扇型布置，所有拉索采用PE保护，自桥面起，中塔100 m，边塔高75 m。从1999年12月大桥建成通车后，在洞庭湖大桥观察到了多次强烈风雨振。中南大学和香港理工大学随即在洞庭湖大桥上进行了大量现场观测与试验研究，探索抑制强烈风雨振的有效方法，并于2002年6月在该桥较长的156根拉索上分别安装了2个磁流变(MR)阻尼器成功抑制了拉索的风雨振［3，6，9，10]。

为了进一步观测拉索风雨振现象，研究组于2003年3月24日至5月11日在现场进行了历时47天的实验研究。如图1所示，本次风雨振观测实验选在岳阳侧边塔A12索，并将其上已安装的MR阻尼器解除。A12 索索长 121.9 m，直径 119 mm，倾角 35.2°，张力3 150 kN，理论第一阶模态频率为1.07 Hz。同时，在岳阳侧边塔顶和桥面各安装1个美国Young＇s公司生产的三向超声风速仪，为了减小塔和桥面对测量风速的影响，塔顶风速仪高出塔顶平面2 m;桥面风速仪在A12号索拉索锚固端处，通过支架伸出桥面边沿4 m、高出桥面1m。塔顶和桥面两风速仪距离水面分别为102 m、26 m，风速仪平行于桥梁轴线方向安装，桥轴线与正北方向大致成 20°交角［3，6]。同时，在拉索距下锚固端L/6(L为索长)处安装了两个加速度传感器，用于测量拉索面内、面外加速度响应。

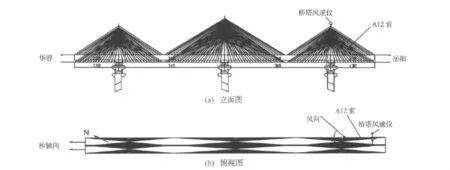
图1 洞庭湖大桥风雨振观测布置(单位:m)Fig.1 Dongting Lake Bridge and development of sensors(Unit:m)

2 实测典型风时变特性

2.1 时变平均风提取

平稳风速模型通常把顺风向风速U(t)看作是在一定时间内不随时间变化的平均风速U(即各态历经的随机过程)和随时间随机变化的顺风向脉动风速u(t)两部分，平均风速对结构产生静态响应，而脉动风速对结构产生动态响应。而非平稳风速模型则认为平均风速不是各态历经的，是时变的。根据Gramer定理，任何一个时间序列都可以分解为时变确定性趋势成分和平稳零均值随机成分，即平稳过程和趋势项。因此，顺风向非平稳风速分解为一个确定性时变平均风速分量和平稳随机的脉动分量叠加的风速非平稳模型［14]:

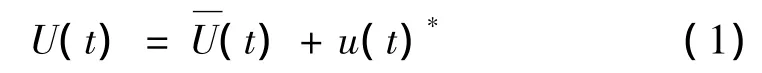
应用非平稳风速模型的关键问题就是趋势项，即时变平均风的提取。目前最为有效的提取时变平均风的方法是经验模态分解(Empirical mode decomposition，EMD)法和小波分析。EMD法将风速信号分解为若干个本征模函数(Intrinsic mode function，简称IFM)和残余函数之和，分解后的残余函数即认为是时变平均风。小波分析则认为正交小波基函数具有能量守恒的性质，即定义单一尺度下的小波能量为该尺度下小波系数的平方和，当风速信号进行小波分解后，某一尺度下能量发生突变时对应的分解层数为最优趋势层数，再利用小波逆变换即可得到时变平均风。申建红等［16]对基于EMD和小波变换提取时变平均风作了较为详细的比较分析，得出基于小波分析的时变平均风较EMD方法更可靠的结论。

本文研究以基于小波分析的方法为主。经分析，在db小波簇、coif小波簇、sym 小波簇中，db10、coif5、sym7分别是本簇中提取时变平均风精度最高的，其中db10小波更优，故本文对风速资料的处理全部使用db10 小波［17]。

2.2 典型风时变特性

现场试验期间，大桥多次发生风雨振，观测系统均进行了采集和记录，采样频率为4 Hz。取桥面及桥塔风速仪分别记录的2003年4月1日16∶51～21∶36，4月1日22∶10～4月2日02∶48两段风速资料作为典型数据，分别称为样本1和样本2，计算基于小波分析和EMD的时变平均风和常数平均风速。为了说明方便，以1小时风速记录为例，图2(a)、图2(b)分别表示以桥面、桥塔于4月1日16:55～17:55记录的1小时风速信号时变风速。从图2可看出，尽管基于小波分析和EMD方法计算的时变平均风不同，但均表明风雨振时桥面及桥塔风速具有明显的非平稳特性。将提取时变平均风速的方法应用到风偏角和风攻角的处理上，得出桥面风偏角基本在在38°～60°之间，塔顶风偏角基本在60°～70°之间，风偏角呈现出明显的非平稳性，如图3(a)所示;桥面风攻角基本在10°左右，塔顶风攻角在20°左右，而风攻角变化很小，非平稳性不明显，如图3(b)所示。

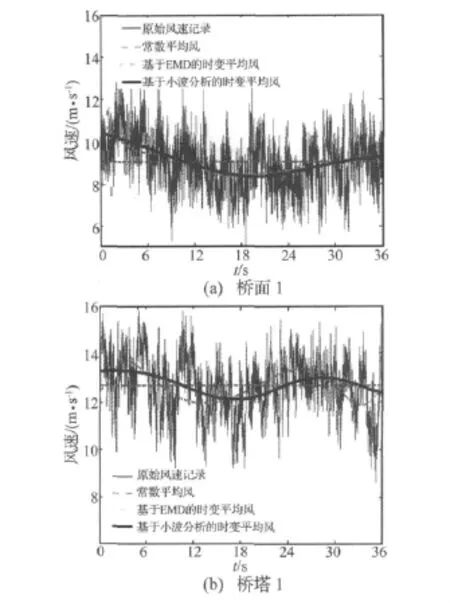
图2 1小时实测风速和时变平均风比较Fig.2 Measured 1h typical wind speed and its time-varying mean wind speed comparison

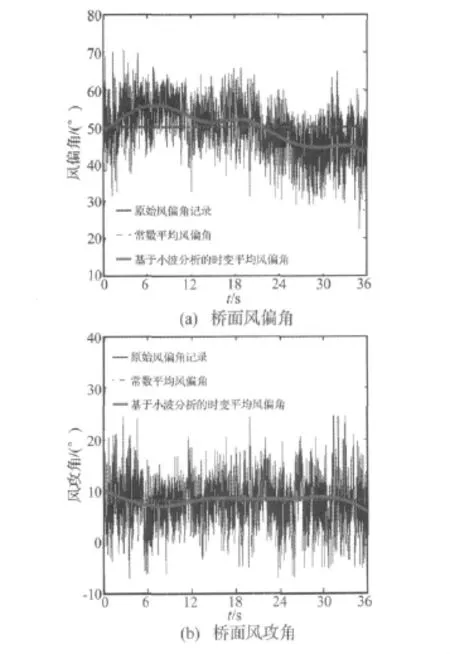
图3 1小时实测风偏角、风攻角和时变平均风偏角、时变平均风攻角Fig.3 Measured 1h typical wind yaw angle and attack angle and their time-varying mean values

3 风场特性分析

3.1 紊流强度

紊流强度是描述风速随时间和空间变化的程度，反映风的脉动的相对强度，是描述大气边界层湍流运动的最重要的特征参数。紊流强度定义为脉动风速的均方差值与平均风速之比。由于实际的风场应包括三个正交方向(顺风向、横风向和竖向)的风速分量及其相关特性的描述，我们首先要将风矢量沿着以平均风矢量为纵向进行空间坐标分解，求出顺风向、横风向和竖向的平均风和脉动风分量，进而求得顺风向、横风向和竖向的紊流强度 Iu、Iv、Iw。

本文分别利用基于小波的非平稳风速模型、基于EMD的非平稳风速模型和传统的平稳风速模型计算紊流强度，计算以1 min为基本时距，各模型紊流强度平均值列于表1。从表1中可看出，基于小波非平稳风速模型的样本1桥面顺风向、横风向和竖向的紊流强度平均值分别为 0.084 6、0.081 5、0.075 7，均分别小于基于EMD非平稳风速模型和平稳风速模型，其它风速记录均有同样结果，表明平稳风速模型确实高估了紊流强度，符合相关研究结论［11]。虽然不同样本风速计算的顺风向、横风向和竖向的紊流强度平均值规律不同，但不同模型计算的同一样本各方向紊流强度则具有相同的规律性，如样本1桥面风速各模型计算结果为Iu＞Iv＞Iw，桥塔则为Iw＞Iu＞Iv，说明分析结果的可靠性。洞庭湖区属于I类场地，按《公路桥梁抗风设计规范》［18]洞庭湖大桥的桥面三方向紊流强度分别为0.13、0.11 和 0.07，桥塔三方向紊流强度分别为 0.10、0.09和0.05，各模型计算的顺风向和横风向紊流强度Iu、Iv小于规范值，但竖向紊流强度Iw则大于规范值。

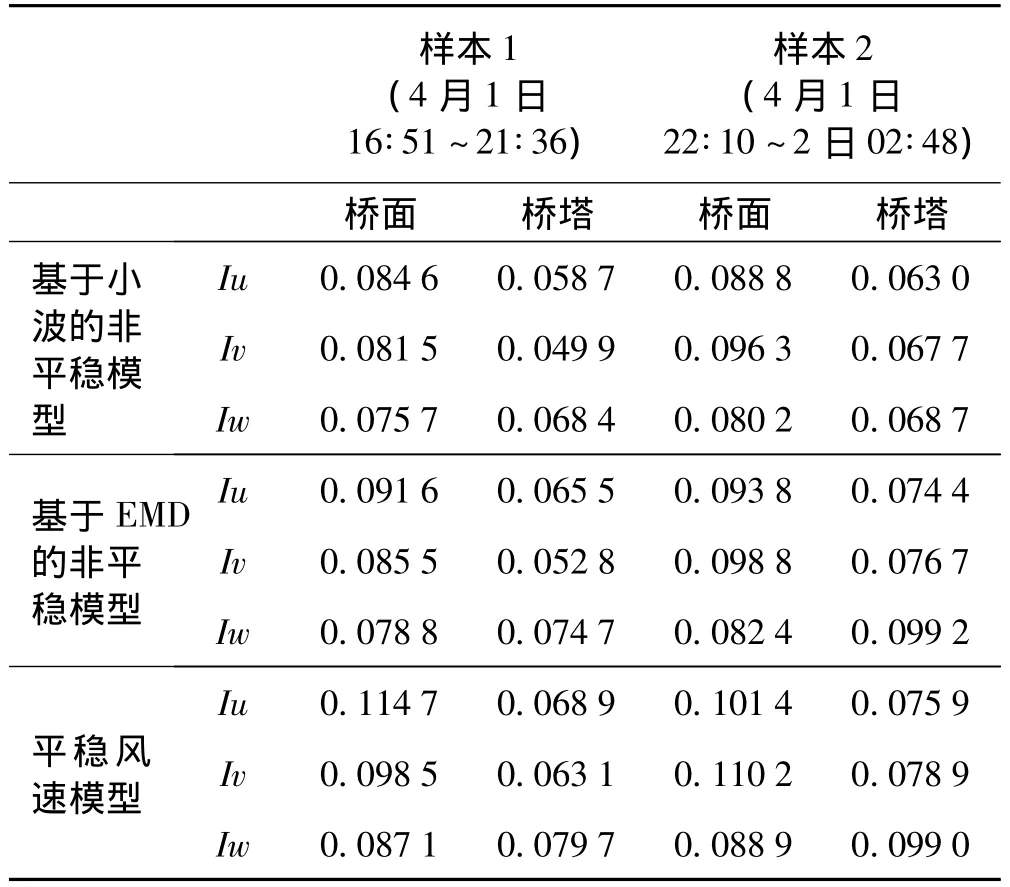
表1 基于不同模型的紊流强度计算值比较Tab.1 Comparison of turbulence intensities based on different wind speed models

3.2 积分尺度

大气湍流运动可以看作是由许多不同的尺度的漩涡运动组合而成的，而不同的尺度的漩涡运动有着不同的特性，在大气边界层中质量、动量和热量的交换过程中起着不同的作用。因此在研究湍流时，定义了湍流积分尺度，用其代表湍流运动中的漩涡的大小。积分尺度是风中旋涡尺寸的量度，也就是在给定方向阵风旋涡的平均尺度。

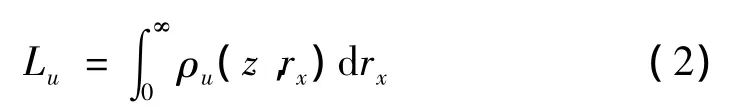
式中，ρu(z，rx)为同一时刻，紊流分量u在顺风向距离为rx的两点测得的互相关函数。因空间多点同时测量往往很难实现，根据泰勒假设，式(2)中顺风向互相关函数 ρu(z，rx)由自相关函数 ρu(z，τ)代替。

基于实测的桥塔、桥面风速样本信号，取1 min为基本时距，运用基于小波分析的非平稳风速模型、基于EMD的非平稳风速模型和平稳风速模型计算的紊流积分尺度平均值列于表2。从表2可看出:整体而言桥面紊流积分尺度小于塔顶紊流积分尺度;不同模型计算的三方向积分尺度平均值几乎为Lu＞Lv＞Lw;三种模型中，运用基于小波分析的非平稳风速模型计算出来的结果最小，EMD次之，而平稳风速模型的计算值最大。运用小波分析和EMD的计算结果相差不大，平均差距8%;而基于小波分析的非平稳风速模型与平稳风速模型的计算结果差距较大，最大差距甚至达到70%，平均差距有45%。

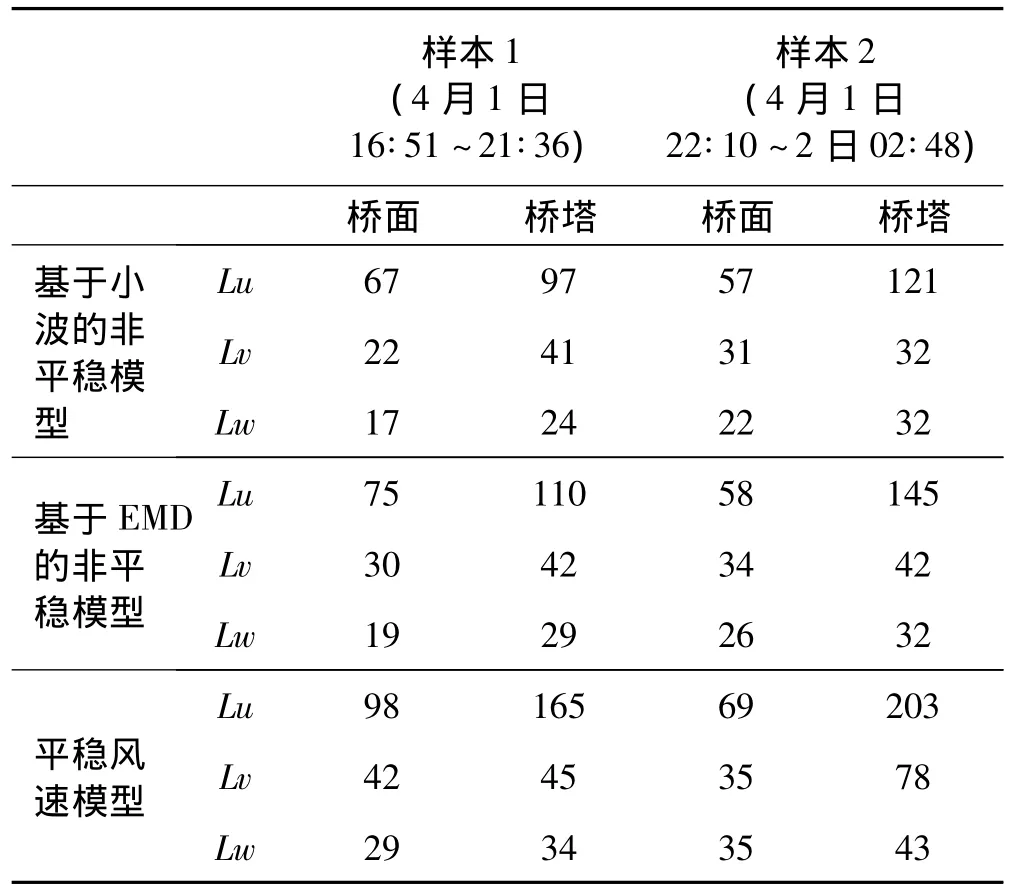
表2 基于不同模型的积分尺度平均值比较Tab.2 Comparison of integral scales based on different wind speed models

3.3 概率密度函数

利用前述同样的实测大桥桥塔、桥面风速样本，基于小波分析的非平稳风速模型、EMD非平稳风速模型和平稳风速模型计算的各样本脉动风概率密度和正态分布拟合如图4所示。从图4中可看出各种模型计算的紊流概率密度函数相对比较接近，基本符合正态分布假设。而样本2桥塔风速计算结果显示出基于小波分析计算的脉动风概率密度相对于其他两种模型更符合正态分布的假定。

3.4 脉动风谱

大气湍流运动是由许多不同尺度的漩涡运动组合而成的，湍流的脉动动能可以认为是由各种不同频率的漩涡产生的贡献。湍流的功率谱密度用来描述湍流中不同尺度漩涡的动能对湍流脉动动能的贡献。顺风向风速分量Ui的频率概率分布可以通过无量纲功率谱密度函数RN(z，n)来表示:

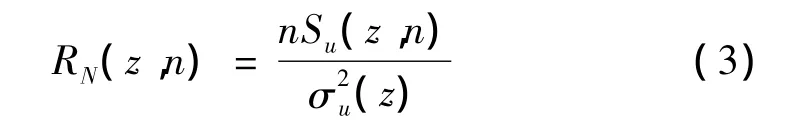
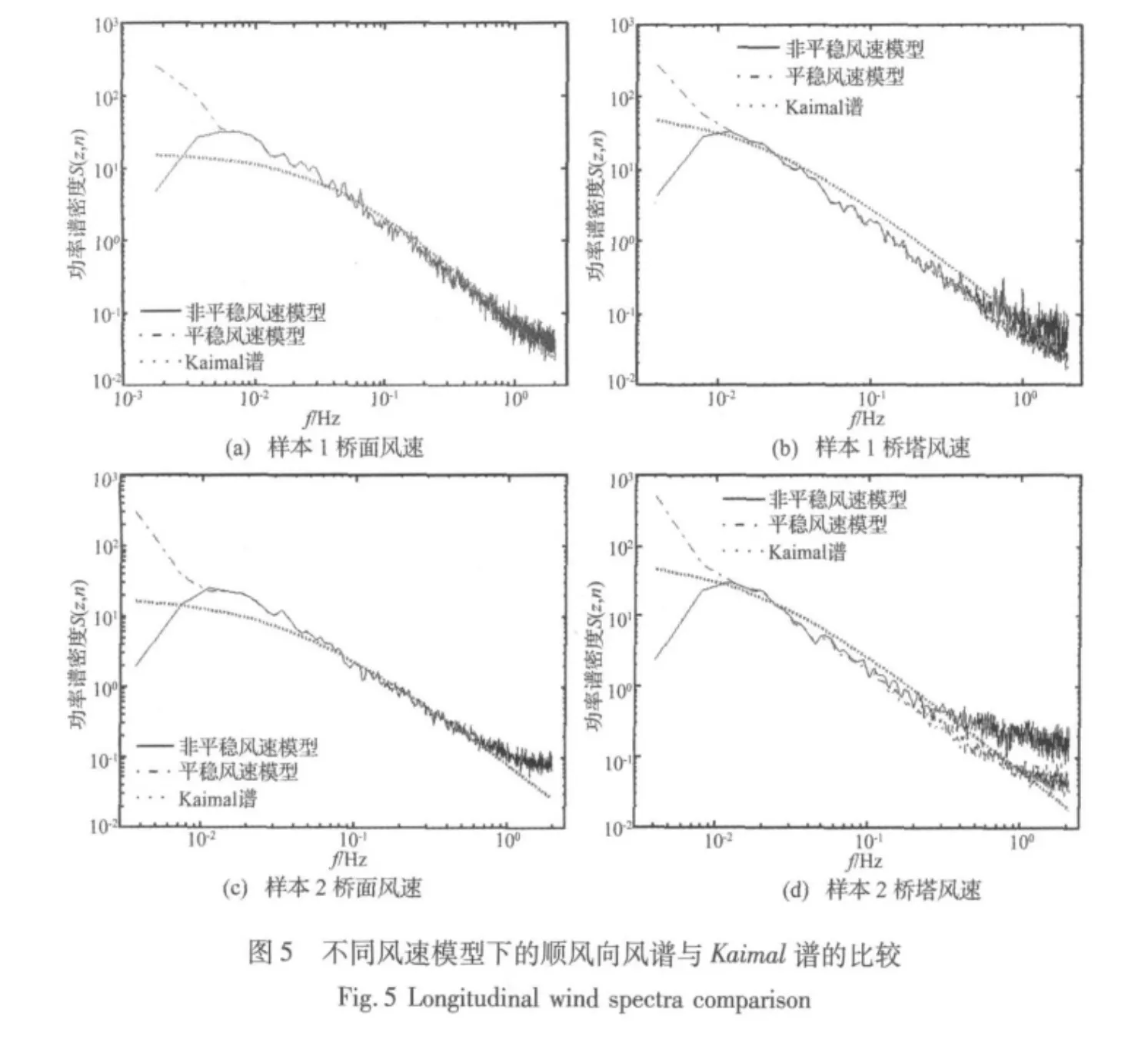
式中，n为频率，Su(z，n)为顺风向脉动分量的功率谱。常用的顺风向风谱有Kaimal谱、Karman谱、Davenport谱以及Simiu谱。目前我国《公路桥梁抗风设计规范》中水平方向风谱采用的是Kaimal谱，其高度Z处平均风速为U的顺风向脉动风功率谱密度函数为:

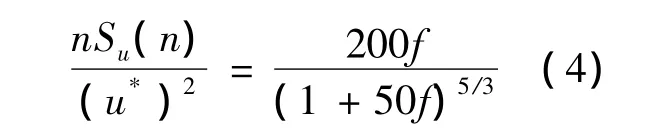
式中，f=nZ/U为莫宁坐标，u*为气流摩阻速度。由于没有u*的测量值，因此采用相应脉动风速分量的方差进行能量归一化为［19]:

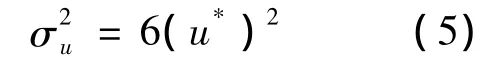
基于小波分析的非平稳风速模型和平稳模型计算的各样本风谱以及Kaimal谱的对比(如图5所示)，可以看出桥面风谱，在低频段(小于0.01 Hz)，基于非平稳风速模型的计算结果小于平稳风速模型，且发展趋势相反，其余频段两种模型计算结果较吻合;对于塔顶风谱，两种模型计算结果仅在中间频段［0.02 Hz，0.1 Hz] 较吻合，其余频段差别较大。另外，由两种模型计算结果与Kaimal谱对比可知，实测洞庭湖大桥风谱与Kaimal谱仅在中间较小频段吻合，高频及低频段均差别较大，各风速样本吻合差别较大，相对而言，桥面风谱吻合稍好些。

竖向较为常用的紊流功率谱密度函数是Panofsky谱:

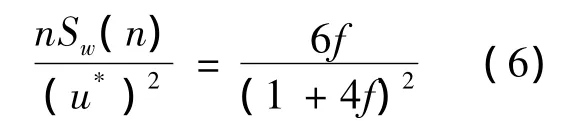
式中Sw(z，n)为竖向脉动分量的功率谱，其余各字母的含义与上式相同。

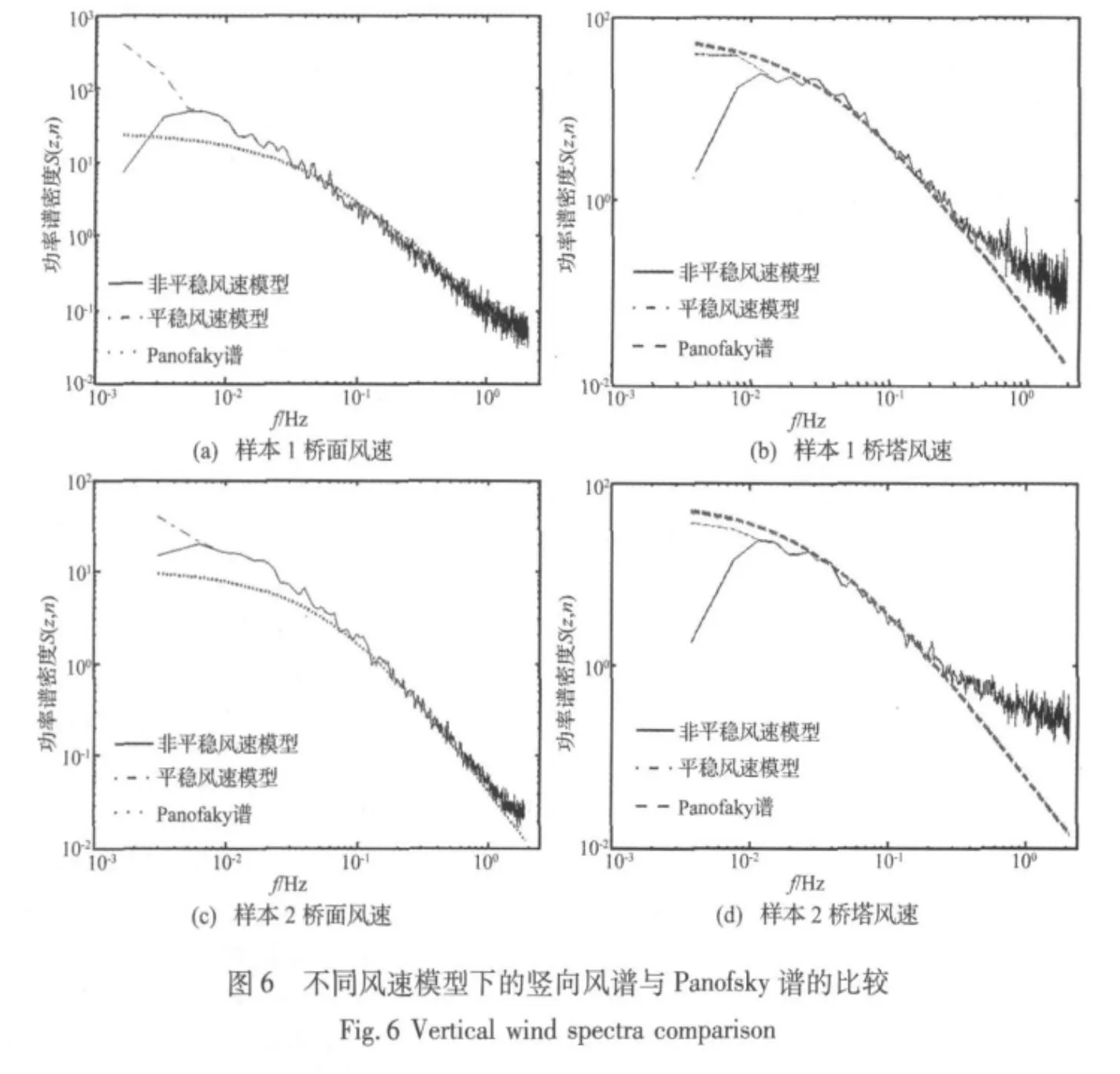
基于小波分析的非平稳风速模型和平稳风速模型计算的各样本风速竖向脉动风谱与Panofsky的比较如图6所示。除了在低频段(小于0.01Hz)外，两种模型计算的桥塔、桥面风谱符合良好;但与Panofsky谱符合差别较大，如对桥面风谱，两种模型计算结果在高频段(大于0.06 Hz)与 Panofsky谱吻合良好，而桥塔风谱则只在中间频段［0.005 Hz，0.12 Hz] 较为吻合，在高频段较Panofsky谱大，在低频段则较Panofsky谱大，且与平稳模型分析结果趋势符合。

由脉动风谱分析结果表明，由于Kaimal谱、Panof-sky谱均不存在拐点，想由式(4)、式(6)就能反映不同强风的功率谱密度是不太现实的，因此若要准确地模拟出桥址区风雨振发生时强风的三维脉动风场，需要提出全新的谱曲线表达式。

4 桥塔、桥面脉动风相关性

空间中任意两点的脉动风速之间存在着不同程度的相关性。在风工程中，一般使用相干系数来表征两点风速的相关性［20]。由于自然风在三维(x，y，z)风场三个方向上的脉动分量间的相关性较弱，实际应用中通常不考虑三个方向之间的相关性，而仅考虑风速在空间上的相关性，从而将理论上三维相关的风速场简化为三个分别沿x，y，z方向的独立的一维风场［21]。本文通过考虑桥塔和桥面两个风速仪记录的顺风向和竖向脉动风量的空间相关性来分析平稳与非平稳风速模型的差别。

风速空间相关性的研究通常采用 Davenport［22]于 1961 年提出的指数形式的相干函数表达式，其给出的简化拟合公式为:

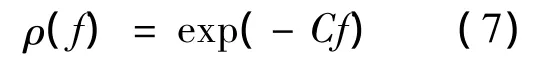
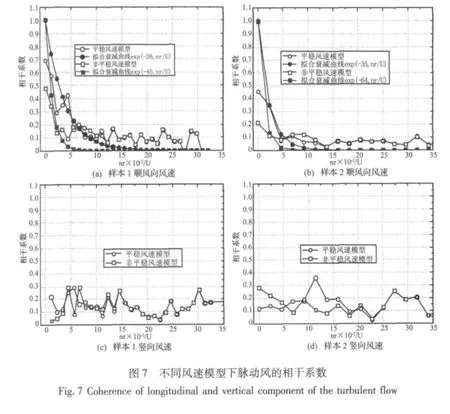
由样本1及样本2实测风速时程计算获得的两测点相干系数曲线如图7所示。从图7(a)，图7(b)顺风向脉动风速相干性曲线中可以明显看出，在低折减频率0～0.1范围内，非平稳风速模型计算得到的风速空间相关性比平稳风速模型值明显偏低，其他折减频率处两种模型相关性基本吻合，由此可以推测通常采用的平稳风速模型过高的估计了低折减频率处的脉动风空间相关性。图7(c)与图7(d)所示的竖向脉动风空间相干曲线中，两种风速模型没有明显趋势性差别，这一现象应该是由于两测点空间距离过大，从而导致竖向脉动风速相关性微弱引起的。

5 结论

风雨振现场观测是桥梁抗风研究中非常重要的研究手段，对实测风场特性和结构风响应准确分析，对认识和抑制拉索风雨振具有重要的价值。本文以洞庭湖大桥2003年4月初发生的强烈风雨振为例，从非平稳角度对实测风速信号及拉索振动响应进行分析，可得出如下结论:

(1)洞庭桥拉索风雨振期间实测风速、风偏角具有明显的非平稳性，而风攻角非平稳性不明显。

(2)采用基于小波的非平稳风速模型对风雨振期间实测风速信号进行紊流强度、积分尺度和概率密度等风场特性分析，通过与基于EMD非平稳风速模型和平稳风速模型分析结果比较，表明非平稳风速模型均较平稳模型合理，更适合用于风雨振非平稳风场特性分析。而两种非平稳风速模型风场特性分析结果相差不大，相对而言，基于小波的非平稳模型分析的紊流强度、积分尺度较基于EMD非平稳模型分析结果稍小，且概率密度更符合正态分布，更加合理。

(3)相比于非平稳风速模型，常用的平稳风速模型在低折减频率范围内过高的估计了脉动风的空间相关性。

本文未考虑导致风雨振的另一重要因素雨流量。文献［6] 已对该桥风速、风向和雨流与拉索振动相关性进行了较为详细的分析，雨流的非平稳性是肯定的。对于风速、风向和雨流非平稳性以及拉索表面水线运动的随机性对拉索风雨振的影响还有待进一步研究。

［1] Hikami Y，Shiraishi N.Rain-wind induced vibrations of cables in cable stayed bridges［J] .Journal of Wind Engineering and Industrial Aerodynamics，1988，29(1 －3):409－418.

［2] Bosdogianni A， Olivari D. Wind-and rain-induced oscillations of cables of stayed bridges［J] .Journal of Wind Engineering and Industrial Aerodynamics，1996，64(2－3):171－185.

［3] 胡建华，王修勇，陈政清，等.斜拉索风雨振响应特性［J] .中国公路学报，2006，19(3):41－48.

［4] Yamaguchi H.Analytical study on growth mechanism of rain vibration of cables［J] .Journal of Wind Engineering and Industrial Aerodynamics，1990，33(1－2):73－80.

［5] Gu M，Du X Q，Li S Y.Experimental and theoretical simulations on wind-rain-induced vibration of 3－D rigid stay cables［J] .Journal of Sound and Vibration，2009(320):184－200.

［6] Ni Y Q，Wang X Y，Chen Z Q，et al.Field observations of rain-wind-induced cable vibration in cable-stayed dongting lake bridge［J] .Journal of Wind Engineering and Industrial Aerodynamics，2007，95(95):303 －328.

［7] Zuo D，Jones N P，Main JA.Field observation of vortex-and rain-wind-induced stay-cable vibrations in a three-dimensional environment［J] .Journal of Wind Engineering and Industrial Aerodynamics，2008，96(6－7):1124－1133.

［8] Main J A，Jones N P，Yamaguchi H.Evaluation of viscous dampers for stay-cable vibration mitigation［J] .Journal of Bridge Engineering，2001，6(6):385－397.

［9] 何旭辉，陈政清，黄方林，等.MR阻尼器在抑制斜拉桥拉索风雨振中的应用研究［J] .湖南大学学报(自然科学版)，2002，29(3):91－95.

［10] Chen Z Q，Wang X Y，Ko J M，et al.MR damping system for mitigating wind-rain induced nibration on dongting lake cable-stayed bridge［J] .Wind and Structures，2004，7(5):293－304.

［11] 张琪昌，李伟义，王 炜.斜拉索风雨振的动力学行为研究［J] .振动与冲击，2010，29(4):173－176.

［12] 方治华，李 晨.斜拉索上瞬时风速与风荷载的数值模拟［J] .振动与冲击，2010，29(7):210－212.

［13] Schroeder J L，Smith D A，Peterson R E.Variation of turbulence intensities and integral scales during the passage of a hurricane［J] .Journal of Wind Engineering and Industrial Aerodynamics，1998，77－78(1－3):65－72.

［14] Xu Y L，Chen J.Characterizing non-stationary wind speed using empirical mode decomposition ［J] . Journal of Structural Engineering ASCE，2004，130(6):9I2 －920.

［15] 孙 海，陈 伟，陈 隽.强风环境非平稳风速模型及应用［J] .防灾减灾工程学报，2006，26(1):52－57.

［16] 申建红，李春祥，李锦华.基于小波变换和EMD提取非平稳风速中的时变均值［J] .振动与冲击，2008，27(12):126－130.

［17] 方 俊.基于小波分析的斜拉桥拉索风雨振非平稳性研究［D] .长沙:中南大学，2010.

［18] 公路桥梁抗风设计规范(JTG/T D60－01－2004)［S] .北京:人民交通出版社，2004.

［19] Simiu E，Scanlan R H，Wind effects on structures［M] .New York:John Wiley＆ Sons，INC，1996.

［20] 阎 启，谢 强，李 杰.风场长期观测与数据分析［J] .建筑科学与工程学报，2009，26(1):37－42.

［21] 李永乐，周述华，强士中.大跨度斜拉桥三维脉动风场模拟［J] .土木工程学报，2003，36(10):60－65.

［22] Davenport A G.The spectrum of horizontal gustiness near the ground in high wind［J] .Quarterly Journal of the Royal Meteorlogical Society，1961，87(372):194－211.