Bloch型空间到Zygmund型空间的广义Cesàro算子和复合算子的积
欧阳小荣
(浙江师范大学数理信息与工程学院,浙江金华321004)
Bloch型空间到Zygmund型空间的广义Cesàro算子和复合算子的积
欧阳小荣
(浙江师范大学数理信息与工程学院,浙江金华321004)
ω和μ是[0,1)上的正规函数,g是单位球Bn上的全纯函数,φ是Bn上的全纯自映射,由g和φ诱导的算从Bloch型空间到Zygmund型空间有界和紧的充要条件.
Bloch型空间;Zygmund型空间;Cesàro算子;复合算子;有界性;紧性
MSC 2000:47B38
0 引言
以Bn={z∈Cn∶|z|<1}表示Cn上的单位球,H(Bn)表示Bn上全纯函数的全体.设z=(z1,…,zn),w =(w1,…,wn)是Cn中的两点,其内积定义为,其径向导数和梯度分别是
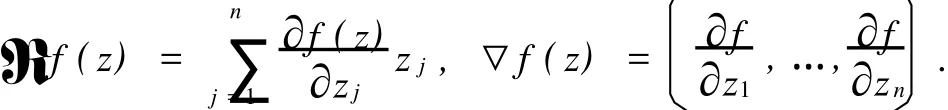
于是,当f∈H(Bn)时其中|α|=α1+α2+…+αn.
给定区间[0,1)上的正值连续函数ω,如果存在0≤δ<1和0 Bn上的Bloch型空间Βω和小Bloch型空间Βω,0分别定义为: 在范数‖f‖Βω=|f(0)|+‖f‖ω下,容易验证Bloch型空间和小Bloch型空间都是Banach空间.对这个空间的研究可见文[1]、[2]等.进一步,若取ω(r)=(1-r2)α,分别取α=1和0<α<1,则Βω是Bloch空间和Lipschitz空间.对Bloch空间和Lipschitz空间的研究可见文[8]、[9]、[10]等. 给定正规函数μ(z)=μ(|z|),Bn上的Zygmund型空间定义为: 其中,μ(z)=μ(|z|).进一步,称f属于小Zygmund空间Ζμ,0,如果f∈Ζμ且满足 容易验证Ζμ和Ζμ,0在范数 下是Banach空间. 设g∈H(Bn),H(Bn)上的广义Cesàro算子Tg定义为: φ=(φ1,…,φn)是Bn上的全纯自映射,复合算子Cφ定义为: 广义Cesàro算子和复合算子的积为: 通过计算有: 其中,ℜφ(z)=(ℜφ1(z),…,ℜφn(z)).以下所出现的φ和ℜφ(z)都如这里所述.若n=1,g=φ,φ(0)=0,该算子就是Volterra型复合算子;若φ(z)=z,该算子就是广义Cesàro算子(见文[4]、[6]、[7]).在文[3],Li首先引入算子TgCφ,并研究了该算子从H∞和Bloch空间到Zygmund空间的有界性和紧性.之后,Li和Stevic在文[10]又研究了该算子在Bloch空间上的有界性和紧性.本文主要研究TgCφ在单位球Bn上从Bloch型空间到Zygmund型空间的算子有界性和紧性.文[3]中的部分结果正好是本文在n=1,ω (r)=1-r2时的结果. 本文涉及的C表示正常数,在不同的位置可表示不同的数.A⋍B表示存在常数C使得 为了研究TgCφ的有界性,我们先引入几个引理.引理1[6]设f∈Βω,则 文章所出现的函数h都如这里所述. 引理2 给定正规函数ω,则h∈H(Bn),|h(z)|≤h(|z|)∈R,z∈Bn.且 进一步,对任意的r∈(0,1),ω(r)⋍ω(r2). 证明 可参见文[5]. 定理1 设g∈H(Bn),φ是Bn上的全纯自映射.则下列各条款等价: (i)TgCφ∶Βω→Ζμ有界; (ii)TgCφ∶Βω,0→Ζμ有界; 证明 (i)⇒(ii)是显然的. (iii)⇒(i).对任意的f∈Βω,有: 由(2)、(3)、(4)、(6)、(7)、(9)式得: 结合(8)式得: (i)⇒(iii).首先,假设TgCφ∶Βω,0→Ζμ有界.令f(z)=1,则(f°φ)(z)=1,ℜ(f°φ)(z)=0,由(8)、(2)式及TgCφ的有界性得: 再令f(z)=z,由(8)、(2)、(10)式知: 对任意w∈Bn,令 其次,设w∈Bn,当|φ(w)|≤δ,δ∈(0,1),显然有: 当δ<|φ(w)|<1时,令 由引理2知, 由TgCφ∶Βω,0→Ζμ有界.故对任意的w∈Bn,有: 定理证完. 定理2 设g∈H(Bn),φ是Bn上的全纯自映射,则TgCφ∶Βω,0→Ζμ,0有界的充要条件是TgCφ∶Βω,0→Ζμ有界,且 成立. 证明 必要性 假设TgCφ∶Βω,0→Ζμ,0有界,则TgCφ∶Βω,0→Ζμ有界,且对任意的f∈Βω,0有TgCφf∈Ζμ,0.取f(z)=1,则 取f(z)=z,则 所以(12)、(13)式成立. 充分性 设p是一多项式,由(13)、(14)式知,当|z|→1时, 所以TgCφp∈Ζμ,0.又因为多项式集是Βω,0中的稠密集,所以对任意的f∈Βω,0,存在多项式列{pk}k∈N*,使得‖Pk-f‖Βω→0,(k→∞).于是,对任意的f∈Βω,0,当k→∞时,由TgCφ∶Βω,0→Ζμ的有界性, 所以TgCφf∈Ζμ,0.由闭图像定理,所以TgCφ∶Βω,0→Ζμ,0有界.定理证毕. 引理3 闭集K⊂Ζμ,0是紧集当且仅当K有界且满足: 证明 类似于文[11]中引理1. 引理4 设g∈H(Bn),φ是Bn上的全纯自映射,有界算子TgCφ∶Βω(Βω,0)→Ζμ是紧算子当且仅当对Βω(Βω,0)中任意有界且在Bn内内闭一致收敛于零的序列{fk}k∈N*有‖TgCφfk‖μ→0(k→∞). 定理3 设g∈H(Bn),φ是Bn上的全纯自映射,TgCφ∶Βω→Ζμ有界.则下列各条款等价: (i)TgCφ∶Βω→Ζμ是紧算子; (ii)TgCφ∶Βω,0→Ζμ是紧算子; 证明 (iii)→(i).设(15)、(16)式成立,则对任意的ε>0,存在δ∈(0,1),当δ<|φ(z)|<1时,有: 由于{fk}与{▽fk}在Bn内内闭一致收敛以及ε的任意性知,当k→∞时, 由引理4知TgCφ∶Βω→Ζμ是紧算子. (ii)→(iii).事实上,(16)式的成立等价于 设{zk}k∈N*是Bn中的序列,满足|φ(zk)|→1(k→∞).令 则fk∈Βω,0,‖fk‖Βω≤C.且 由(5)和(2)式得: 由TgCφ的紧性可得(16)式. 对上述的{zk},令 于是,由引理2得: 由于TgCφ的紧性和(16)式成立,得: 定理证毕. 定理4 设g∈H(Bn),φ是Bn上的全纯自映射,则下列各条款等价: (i)TgCφ∶Βω→Ζμ,0是紧算子; (ii)TgCφ∶Βω,0→Ζμ,0是紧算子; 证 (i)→(ii)是显然的. (iii)→(i).由引理3知,TgCφ∶Βω→Ζμ,0是紧算子当且仅当 设‖f‖Βω≤1,由(19)、(20)式得: 所以TgCφ∶Βω→Ζμ,0是紧的. (ii)→(iii).假设TgCφ∶Βω,0→Ζμ,0是紧的,则TgCφ∶Βω,0→Ζμ是紧算子.由定理3(15)式知,对任意的ε>0,存在δ∈(0,1),使得当δ<|φ(z)|<1时,有: 因为TgCφ∶Βω,0→Ζμ,0是紧算子,所以TgCφ∶Βω,0→Ζμ,0有界,由定理2知: 故对上述的ε,存在r∈(0,1),使得当r<|z|<1时,有: 因此,当δ<|φ(z)|<1,r<|z|<1时, 当|φ(z)|≤δ,r<|z|<1时, 由(21)、(22)式及ε的任意性可得(15)式.同样的方法可得到(16)式.证毕. 致谢:衷心感谢胡璋剑教授的精心指导. [1]ZHU K H.Spaces of Holomorphic Functions in the Unit Ball[M].New York:Springer,2005:79~103. [2]COWEN C C,MACCLUER B D.Composition Operators on Spaces of Analytic Functions[M].Boca Raton:Studies in Advanced Mathematics,CRC Press,1995:15~94. [3]LI S X,STEVO S.Products of Volterra type operator and composition perator fromH∞and Bloch spaces to Zygμnd spaces[J].J Math Anal Appl,2008(345):40~52. [4]HU ZJ.Extended Cesgrave aro operators on the Bloch space in the unit ball ofCn[J].Acta Math Sci Ser B Engl Ed, 2003,23(4):561~566. [5]HU ZJ,WANG S S.Compositions operators on Bloch-type spaces[J].Proc Royal Soc Edinburgh,2005(135):1229~1239. [6]TANG X M.Extended esgrave aro operators between Bloch-type spaces in the unit ball ofCn[J].J Math Anal Appl, 2007(326):1199~1211. [7]ZHOU Z H,ZHU M.Extended Cesàro operators between generalized Besov spaces and Bloch type spaces in the unit ball[J].Journal of Function Spaces and Applications,2009,7(3):209~223. [8]FL ETT TM.Lipschitz spaces offunctions on the circle and the disc[J].J Math Anal Appl,1972(39):125~158. [9]JANSON S.Generalization on Lipschitz spaces nd applications to Hardy spaces and bounded mean oscillation[J].Duke Math J,1980(47):959~982. [10]LI S X,STEVO S.Products of inegral-type operators and composition operators between Bloch-type spaces[J].J Math Anal Appl,2009,49(2):596~610. [11]MADIGAN K,MATHESON A.Compact composition operators from Zygund spaces into Bloch spaces[J].Trans A-mer Math Soc,1995(347):2679~2687. Products of ExtendedCesàroOperator and Composition Operator fromBloch-typeSpaces toZygmund-typeSpaces OU YANG Xiao-rong Letωandμbe normal function,gbe holomorphic function on the unit ball andφbe holomorphic self-mapping ofBn.The operatorTgCφ∶Bω(Bω,0)→Zμ(Zμ,0)induced bygandφ,defined byTgCφfditions for the operatorTgCφfromBloch-ty pespaces toZy gmund-ty pespaces. Bloch-ty pespaces;Zy gmund-ty pespaces;extended Cesàrooperator;composition operator O175.14 A 1009-1734(2011)01-0018-07 2010-10-24; 2010-11-12 国家自然科学基金项目(10771064);浙江省自然科学基金项目(Y7080197,Y6090036,Y6100219). 欧阳小荣,浙江师范大学数理信息与工程学院2008级在读硕士,从事函数论研究. MSC 2000:47B38


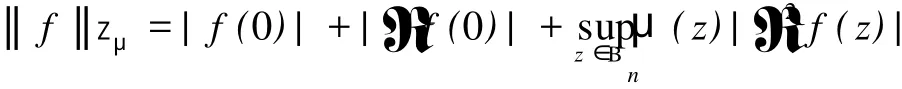
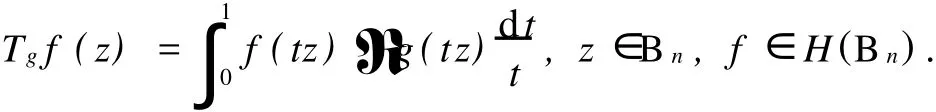
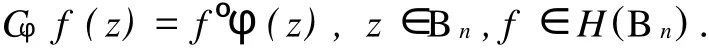


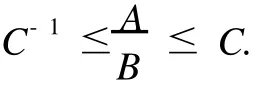
1 TgCφ的有界性
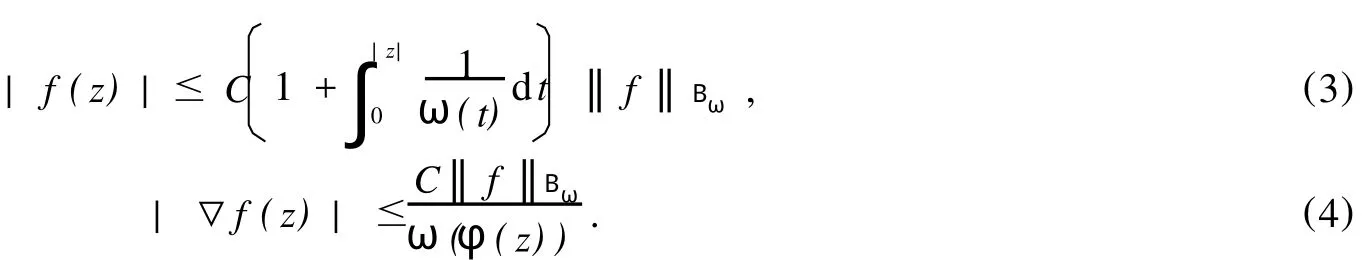
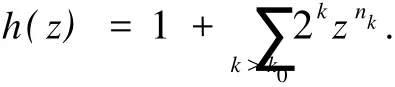
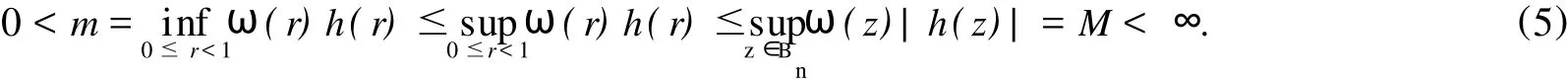
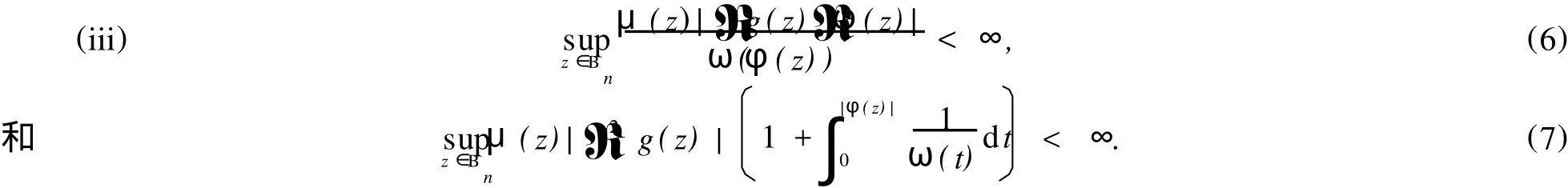


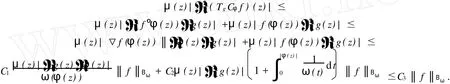




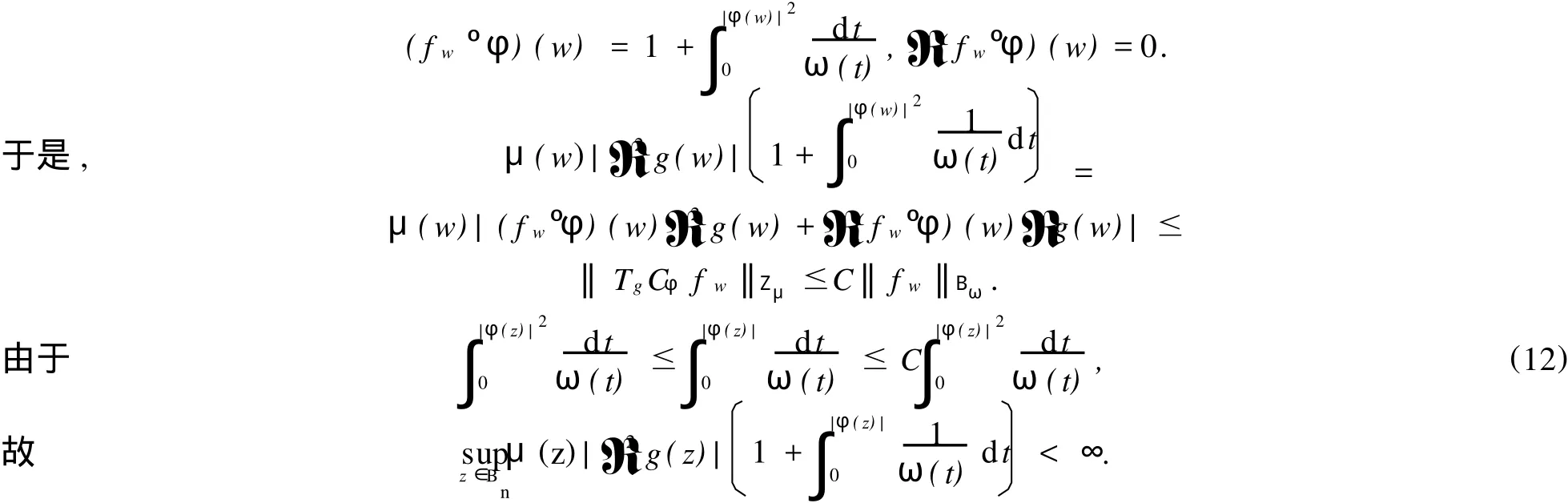
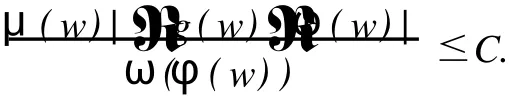
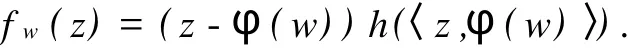
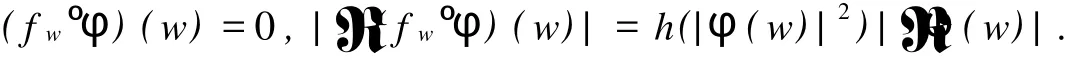
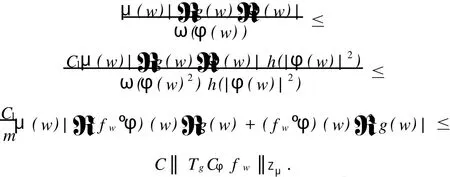
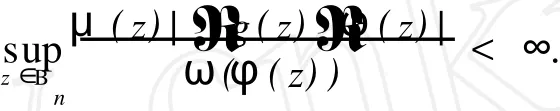

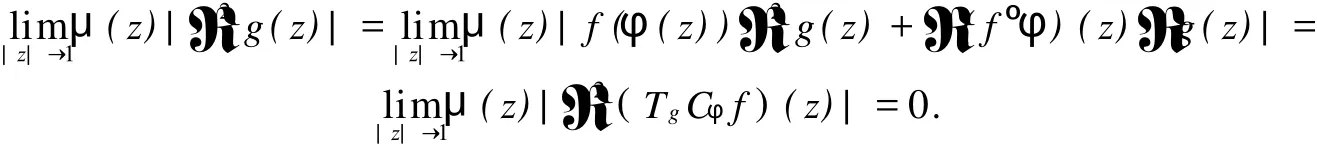
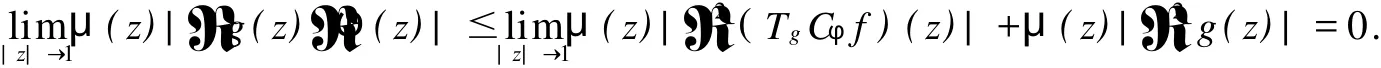
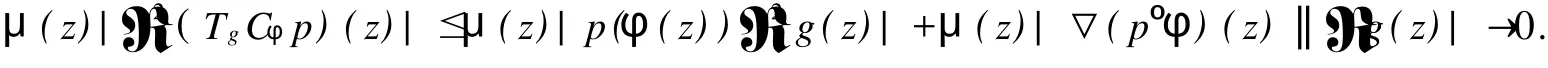
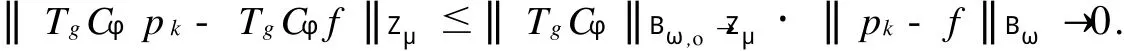
2 TgCφ的紧性
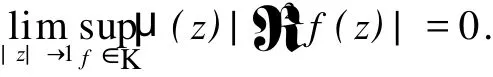
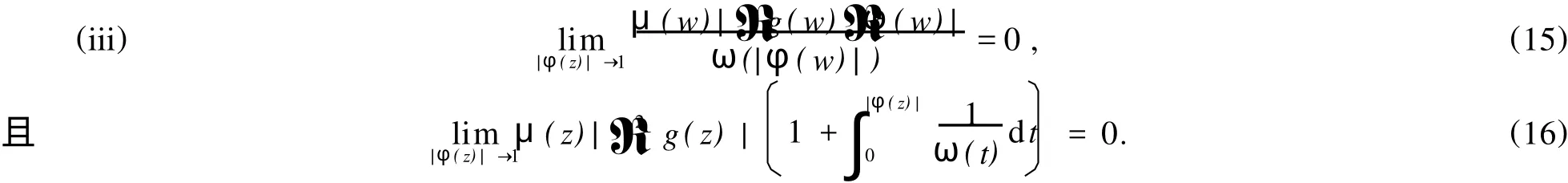
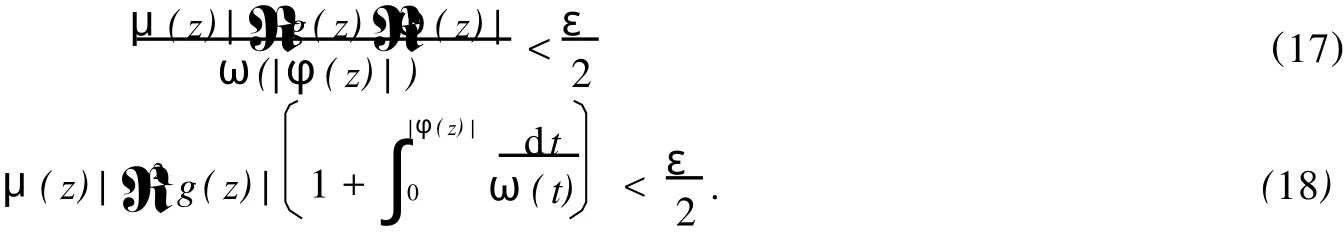
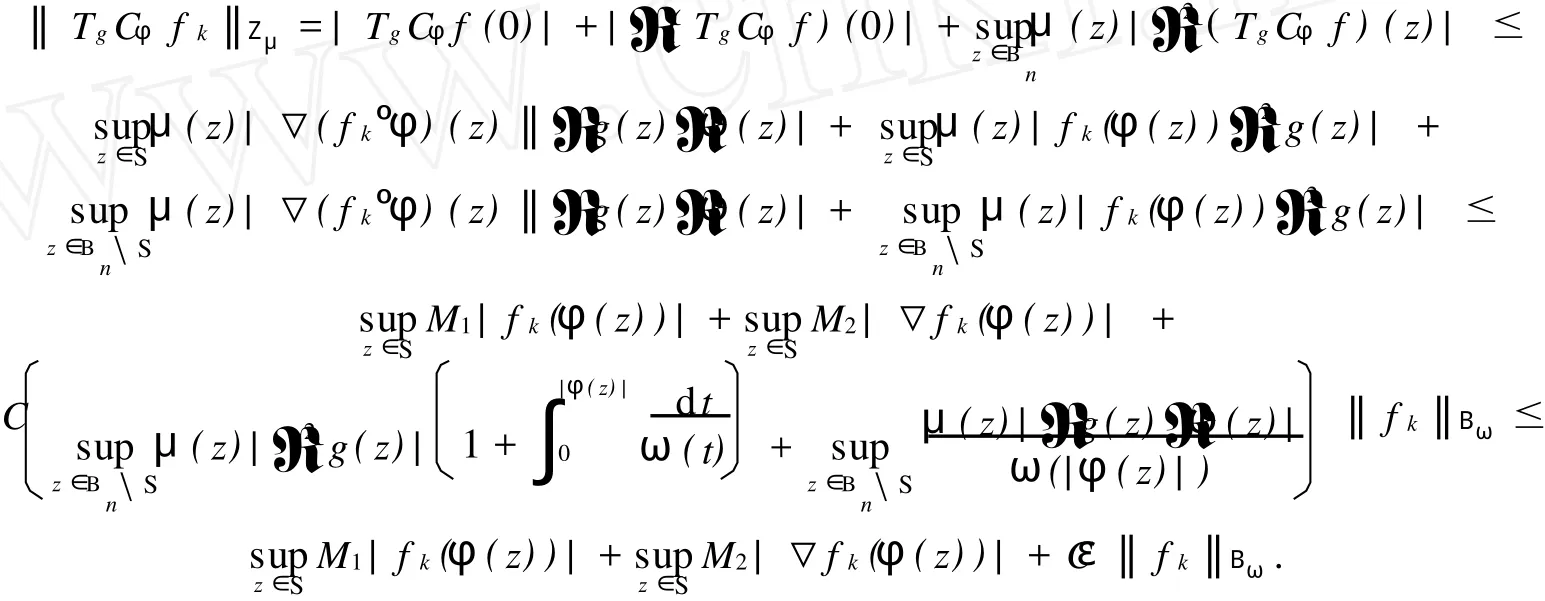

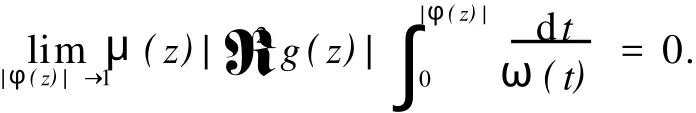
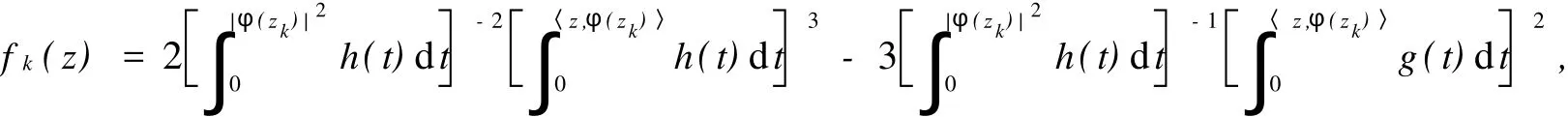

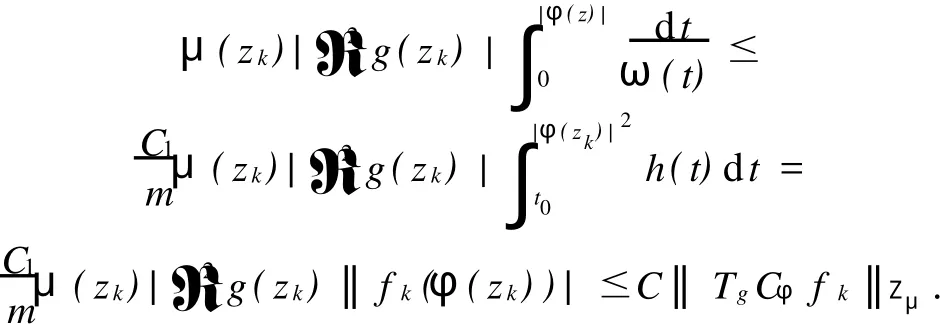



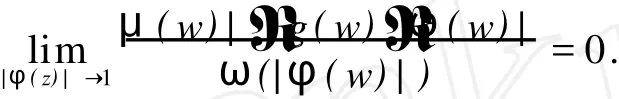
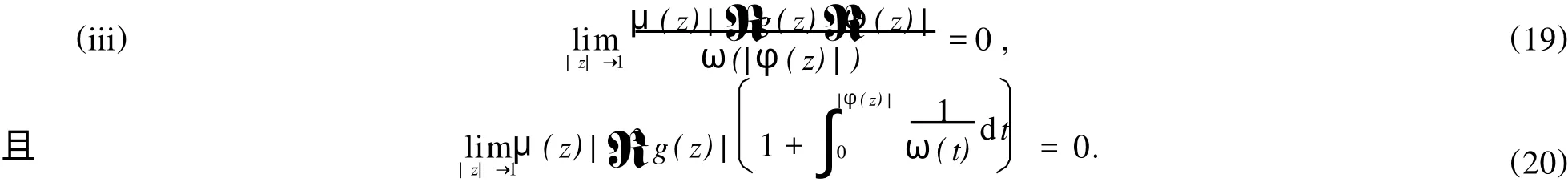


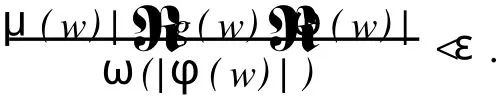

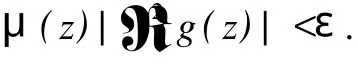

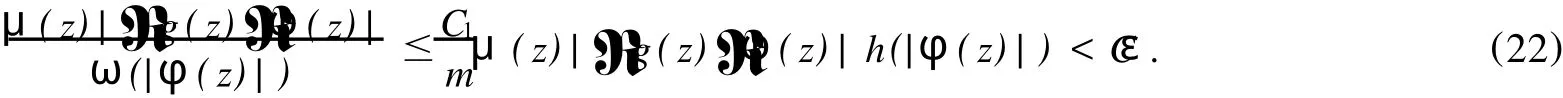
(College of Mathematica,Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China)

