基于记忆电阻的Chua混沌电路的实现及动态性能分析

齐爱学,卞 丽,李卫兵

(滨州学院物理与电子科学系,山东滨州256600)

基于记忆电阻的Chua混沌电路的实现及动态性能分析

齐爱学,卞 丽,李卫兵

(滨州学院物理与电子科学系,山东滨州256600)

提出利用磁通量控制的记忆电阻和1个负电导来替代典型蔡氏混沌电路的非线性电阻,并对改进后电路的理论推导、数值仿真、分岔图、lyapunov指数谱等系统的基本动力学特性进行分析,结果显示,该系统可由马蹄混沌吸引子过渡为双涡卷混沌吸引子,混沌行为更为复杂。最后,利用FPGA技术实现了该电路,实验结果表明,该系统能够产生混沌吸引子。

记忆电阻;蔡氏混沌电路;混沌吸引子;FPGA电路

记忆电阻做为电路的第4个基本电路元件,1971年被LEON O.CHUA提出[1],2008年5月Williams[2]等人在实验室证实了记忆电阻后,其应用价值引起了国内外许多学者的兴趣[3-7],发现利用记忆电阻的数字工作方式,可以作为非易失性阻抗存储器(RRAM);利用记忆电阻的模拟工作模式,可以制作新型的模拟式计算机。

近来,蔡少棠采用1个特性曲线为单调上升且分段线性的非线性记忆电阻替换蔡氏振荡器中的蔡氏二极管,导出了一系列基于记忆电阻的振荡器电路[3-4];包伯成采用1个由光滑3次单调上升的非线性函数来描述的记忆电阻替换蔡氏二极管,获得1个年Bharathwaj Muthuswanmy利用模拟电子电路硬件实现了记忆电阻蔡氏混沌电路[5]。记忆电阻在混沌电路中的应用实现成为国内外许多专家研究的热点。

混沌和超混沌理论的研究和应用是近年来国内外许多专家研究的热点,利用记忆电阻实现混沌电路成为近来人们研究的热点[5,7-9]。目前的研究只是利用Matlab仿真实现记忆电阻混沌信号的产生,本文提出通过FPGA对记忆电阻蔡氏混沌电路硬件实现,根据记忆电阻的结构,利用磁通量控制的记忆电阻来替代典型蔡氏电路的非线性电路,并对替换后的电路进行了动力学分析,通过分析发现,该系统仅存在1个平衡点,且该平衡点是1个不稳定的鞍焦点。通过数值仿真验证,该系统随着参数的变化,相平面轨迹由马蹄混沌吸引子过渡到双涡卷混沌吸引子。混沌行为不同于其他动力学系统[10-12],混沌行为更为复杂。

1 记忆电阻实现的基本的Chua's混沌电路

记忆电子是1个无源二端电子器件,两端的电压u和流经记忆电阻的电流i满足如下关系[1]:

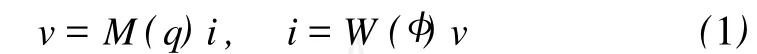
其中M(q)称为记忆电阻,W(φ)称为记忆电导。定义为:

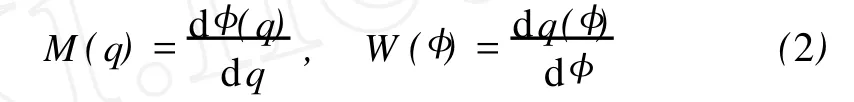
上式表示函数φ(q)和q(φ)的斜率,M(q)和W(φ)称为记忆电阻的本构关系。

非线性记忆电阻满足单调递增和逐段线性的特点,即满足如下关系式:

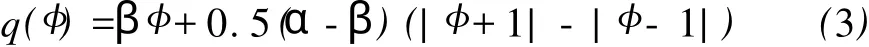
式中α,β>0,则

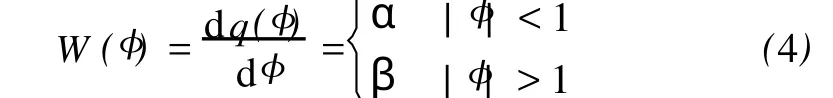
图1 Chua's混沌电路模型Fig.1 Chua's chaotic circuit

对典型的蔡氏混沌电路如图1(a)所示对其电路进行修改,用磁通量控制的记忆电阻来代替蔡氏混沌电路中的非线性电阻,并在电路中增加一个负电导G,如图1(b)所示,得如下微分方程:

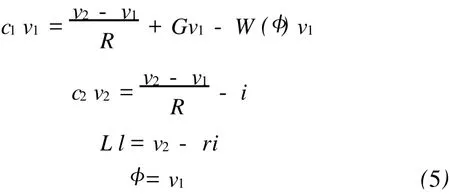
式中

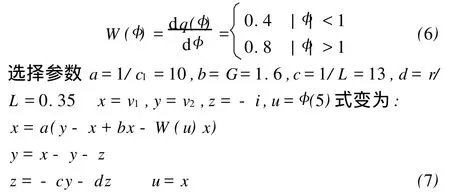
在系统(7)满足上述参数情况下,在初始条件为(0,0.3,0,0)时,系统的相平面轨迹双涡卷的混沌吸引子,对应的相平面轨迹和时序图见图2。

图2 记忆电阻蔡氏混沌电路相平面轨迹及时序图Fig.2 Phase portrait and time series of memristor Chua’s chaotic circuit

2 系统的动力学分析

2.1 平衡点及稳定性分析

对系统(7)的动力学特性进行分析,发现该系统仅存在1个平衡点为:A={(x,y,z,u)|x=y=z=0,u= cons tant},在平衡点A处对系统(7)进行线性化,得到系统的Jacobian矩阵为:

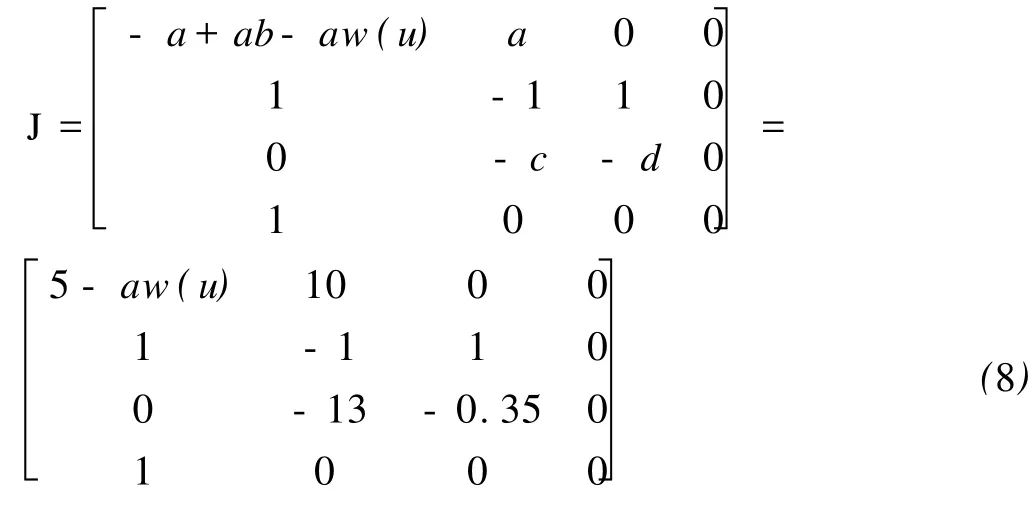
式中,a,b,c,d是常数,当|u|>1时,w(u)=0.8;当|u|< 1时,w(u)=0.4。

令det(J-λE)=0,解得Jacobian矩阵有2组相应的特征根;

当|u|>1时,解得相应的特征根为ρ1=0,ρ2,3= 0.078 7±2.846 6i,ρ3=-4.507 3

当|u|<1时,解得相应的特征根为ρ1=0,ρ2,3= -1.278 0±2.450 5i,ρ3=2.206 0

有特征根可知,该系统在平衡点A处是1个不稳定的鞍焦点。

2.2 系统的耗散性和吸引子存在性分析

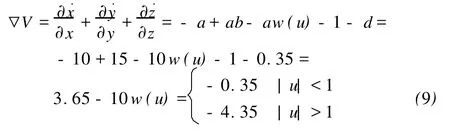
参数a=10,b=1.5,c=13,d=0.35时,系统以指数形式收敛:

当t→∞时,混沌轨迹的的每个体积元以指数率-0.35或-4.35收缩到0,所有系统轨迹线最终会被限制在一个体积为0的集合上,其渐进运动将被固定在1个吸引子上。

3 分岔分析

随着系统参数的改变,系统平衡点的稳定性将会发生变化,从而使得系统也将处于不同的状态。通过Lyapunov指数谱图和分岔图,如图3(a)和(b)所示,可以很直观的分析出系统参数变化时系统状态的变化情况。

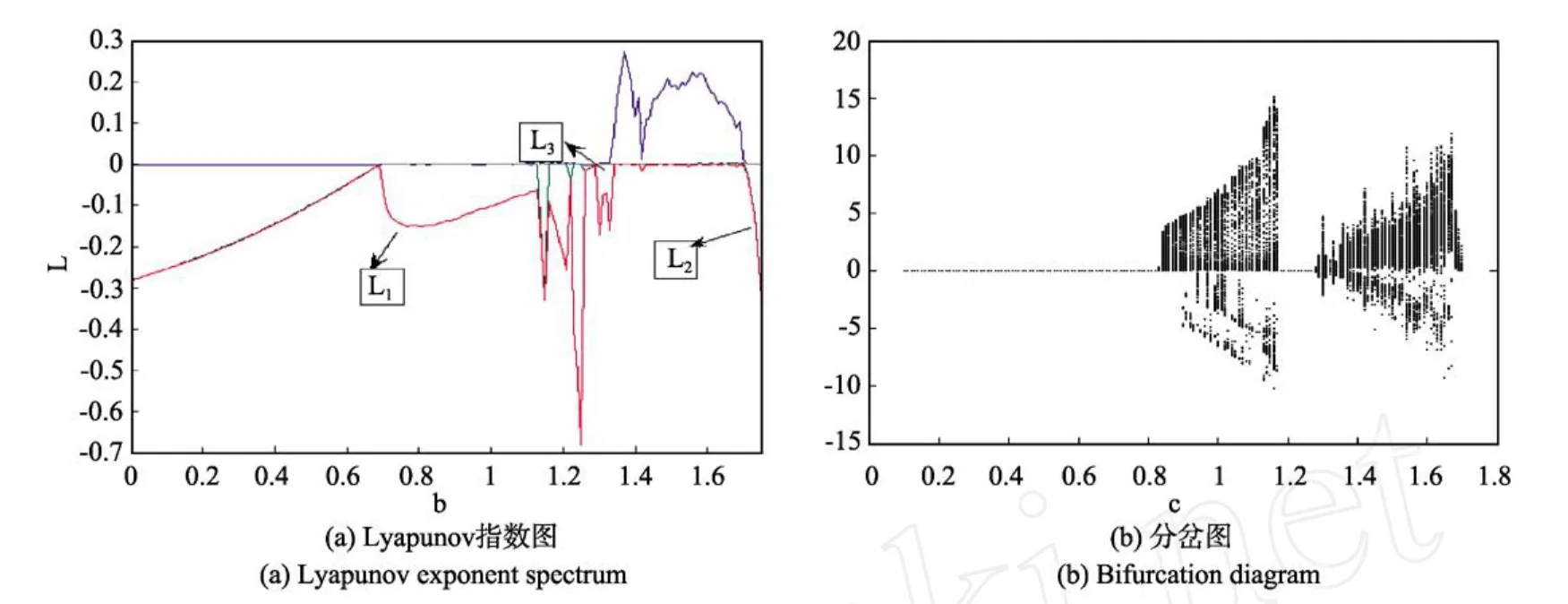
图3 系统的分岔图和Lyapunov指数图Fig.3 Lyapunov exponent spectrum and bifurcation diagram of system

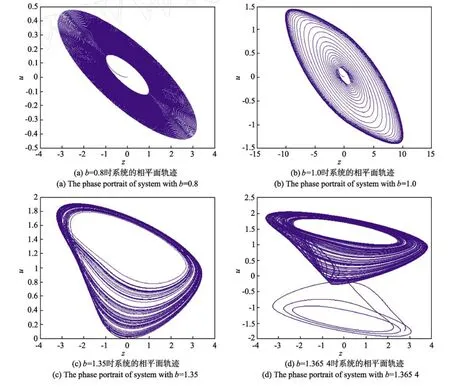
图4 a=10,c=12,d=0.35下,b∈(0.78:1.695),系统的相平面轨迹Fig.4 the phase portrait of system witha=10,c=12,d=0.35 andb∈(0.78:1.695)

固定参数a=10,c=13,d=0.35,在初始条件为(0,0.3,0,0)时,系统随参数b变化时,可以看出,该系统在参数b∈(0.78～0.806)之间,该系统是周期的,系统的相平面轨迹为极限环,如图4(a),系统存在多个周期窗口,b∈(1.13～1.16)∪(1.21～1.23)∪(1.25～1.33)。参数b∈(0.807～1.12)之间,系统是拟周期的,系统的相平面轨迹如图4(b)所示;参数b∈(1.33～1.365)时,在短暂的时间内,系统的相平面轨迹是马鞍形状的混沌吸引子,如图4(c)所示;当参数b=1.365 4时,有马鞍形混沌吸引子向双涡卷混沌吸引子过渡,相平面轨迹如图4(d)所示;当参数b∈(1.365 5～1.695)系统的相平面轨迹时双涡卷的混沌吸引子,如图2(a)～(c)所示。在参数为a=10,c=13,d=0.35,b=1.43时,系统具有较大的正Lyapunov指数,其值为L1= 0.282 4。

4 记忆电阻蔡氏混沌电路FPGA硬件实现

近来,Bharathwaj Muthuswanmy利用模拟电路实现记忆电阻蔡氏混沌电路产生混沌吸引子[5],本文利用数字电路中的FPGA技术来实现记忆电阻蔡氏混沌电路。该电路所使用的开发平台是AL TERA公司开发的QUARTUS II 7.0和DSPBUILDER 7.0。该软件开发平台的主要特点就是能够直接利用Simulink来调用DSP Builder库中的各个单元,从而便于电路模块化设计和FPGA硬件实现[6]。

由于本电路是针对数字信号进行处理的,这就要求首先要对连续时间系统(7)进行离散化处理,得离散化后的差分方程[11]:

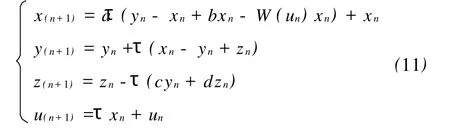
式中各个参数仍然等同于系统(7)的参数,τ为离散采样时间步长,本文选取τ=0.001。

为了用FPGA技术实现系统(11),如图5所示。首先利用DSP Builder创建1个MDL文件,经仿真验证满足设计需要后,经信号编译器(Signal Compiler)将MDL文件转换为VHDL文件和QPF文件,再对QPF文件进行分析、综合和编译,通过J TAG端口将代码下载到型号为EP2C35F484C8的芯片中,经D/A转换器,将FPGA输出的数字信号转换成模拟信号,用示波器观测记忆电阻蔡氏混沌电路中的混沌吸引子如图6所示。通过比较FPGA硬件实验结果和仿真实验结果,实验结果符合的很好。

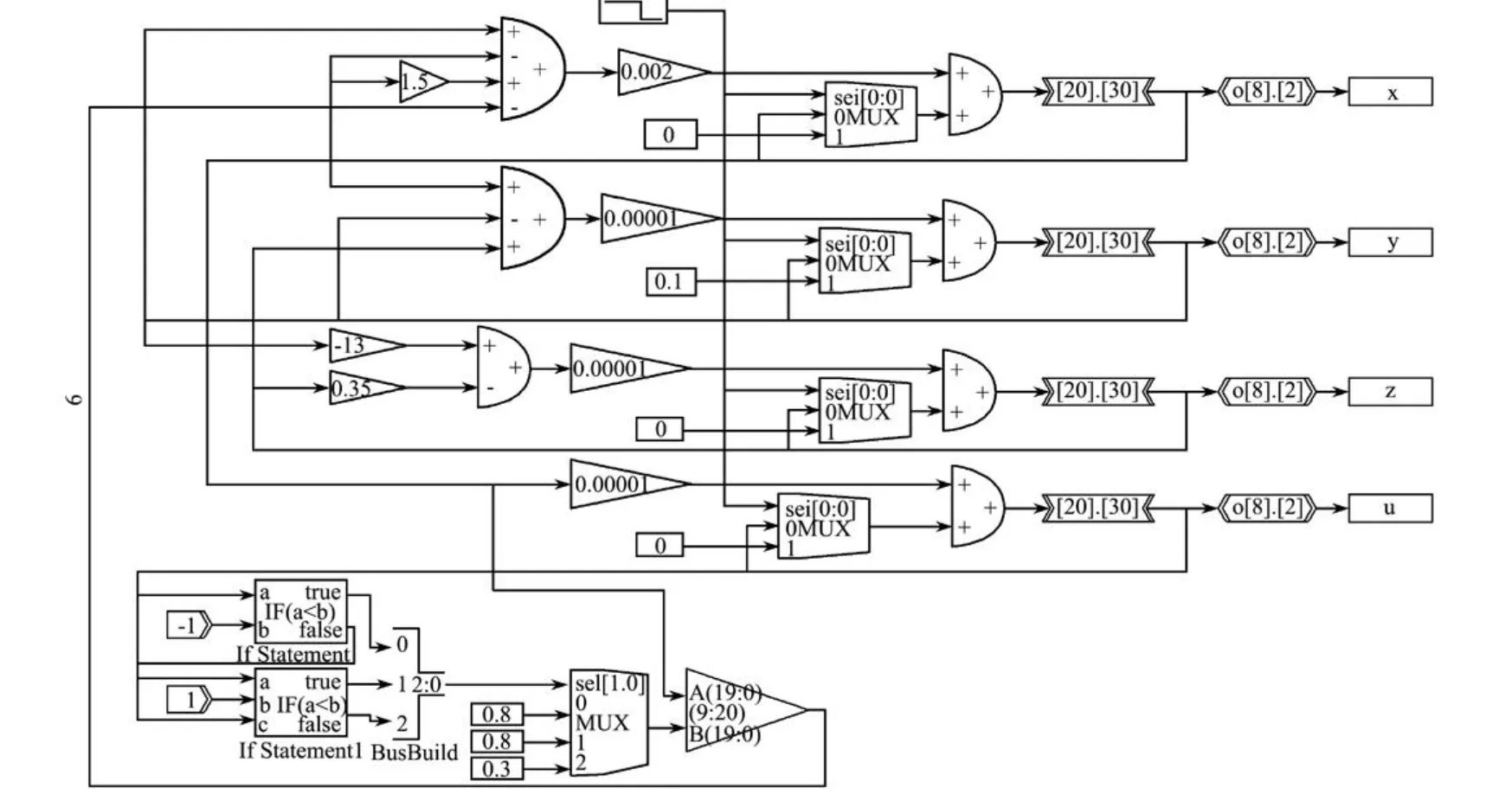
图5 记忆电阻蔡氏混沌电路的FPGA实现Fig.5 FPGA implementation of memristor chua’s chaotic circuit

图6 FPGA实现的记忆电阻蔡氏混沌相平面轨迹Fig.6 Phase portrait of memristor chua's chaos based on FPGA implmentation

5 结语

本文提出利用磁通量控制的记忆电阻和1个负电导替代典型蔡氏混沌电路中的非线性电阻元件,得到1个新的混沌系统,通过对其动力学特性分析、数值仿真、FPGA硬件实现显示,该系统能够产生短暂的马蹄形混沌吸引子和双涡卷混沌吸引子,系统的混沌行为更为复杂,可以用来产生混沌序列,应用于通信保密和图像加密等领域。

[1] Leon O.CHUA.Memristor—the missing circuit element[J].IEEE Transactions on Circuit Theory,1971,CT-18(5):507-519.

[2] Dmitri B.Strukov,Gregory S.Snider,et al.The missing memristor found[J].Nature,2008,453(1):80-83.

[3] Wang Xiao-bin,Chen Yiran,Li Hai,et al.Spinteonic memristor throungh spin-torque-induced magnetization motion[J].IEEE E-lectron Device Letters,2009,30(3):294-297.

[4] Yang J J,Pickett M D,Li X,et al.Memristor switching mechanism for metal/oxide/metal nanodevices[J].Nature Nano-technology,2009(3):429-433.

[5] Bao Bo-heng,Liu Zhong,Xu Jianping.Transient chaos in smooth memristor oscillator[J].Chin Phys B,2010,3(19):0305101-0305106.

[6] Ding Qun,Pang Jing,Fang Jin-qing,et al.Designing of chaotic system output sequence circuit based on FPGA and its Applications in Network[J].International Journal of Innovative Computing, Information and Control,2007,3(2):449-456.

[7] Yuriy V,Pershin,Massimiliano Di Vertra.Memristive circuits simulate memcapacitors and meminductor[J].Physics.ins-det,2009,10 (1):1-2.

[8] Makoto Itoh,Leon O.Chua Memristor oscillators[J].International Journal of Bifurcation and Chaos,2008,18(11):3183-3206.

[9] Bharathwaj Muthuswanmy,Pracheta Kokate.Memristor based chaotic circuits[J].IETE Technical Review,2009,26(6):417-429.

[10] Bharathwaj Muthuswanmy.Implementing memristor based chaotic circuits[R].Technical Report No.UCB/EECS-2009-156, 2009,11:1-11.

[11] Wang Guangyi,He Hailian.A new rosslor hyperchaotic system and its realization with systematic circuit parameterdesign[J]. Chin Phys B,2008,17(11):4014-4121.

[12] Wang Guangyi,Bao Xulei,Wang Zhonglin.Design and FPGA implementation of a new hyperchaotic system[J].Chin Phys B, 2008,17(10):3596-3607.

Abstract: The paper presents a new oscillator,which is derived from Chua’s oscillator by replacing Chua’s diode with a fluxed-controlled memristor and a negative conductance.The basic dynamical properties of the improved circuit are analyzed via theoretical analysis and numerical simulation using the Lyapunov exponent spectrum and bifurcation diagram.The results shown that the system can turn from the 2-scroll chaotic attractor chaotic attractor to saddle chaotic attractor,which chaotic behaviors are more complex.The circuit is designed and realized based on FPGA(field programmable gate array).Comparing the experimental results with the numerical simulation,the two are the very same,and be able to generate chaotic attractor.

Key words: memristor;Chua's chaotic circuit;chaotic attractor;FPGA circuit

责任编辑 陈呈超

Realization of Chua's Chaotic Circuit Based on the Memristor and Dynamic Performance Analysis

QI Ai-Xue,BIAN Li,LI Wei-Bing
(Department of Physics and Electronic Science Binzhou University,Binzhou 256600,China)

TN901

A

1672-5174(2011)06-119-06

国家自然科学基金项目(30400335)资助

2010-07-15;

2011-03-19

齐爱学(1974-),女,副教授。E-mail:aixuebz@126.com