两类本原不可幂定号有向图基的界❋

胡红萍

(中北大学 理学院,山西 太原 030051)

0 引 言

元素取自于集合 {+,-,0}的矩阵称为符号模式矩阵,简称符号模式.Qn表示所有 n×n的符号模式的集合.设 A=(aij)∈Qn,则 A的定性矩阵类定义为 Q(A)={B∈Mn(R)|sgn(B)=A}.类似于普通矩阵的运算,符号模式矩阵也具有相应的运算,都归结为元素的运算,即+,-,0的运算形式;但当“+”加“-”时,会出现“未定元”,记作#.称集合Γ={+,-,0,#}为广义符号集,元素取自于集合Γ的矩阵称为广义符号模式矩阵,简称广义符号模式.

设 A=(aij)∈ Qn是 n阶符号模式,顶点集为 V={1,2,… ,n}和弧集为 E={(i,j)|aij≠0}的有向图称为 A的伴随有向图(可能有环),记为 D(A).将 D(A)中每条弧(i,j)赋予 aij得到的图称为 A的伴随定号有向图,记为 S(A).反过来,给出一个 n阶定号有向图 S,一定存在 n阶符号模式矩阵 A,使得 A的伴随定号有向图是 S.因此符号模式矩阵和定号有向图之间存在一一对应的关系.

设 D是有向图,若(i0,i1),(i1,i2),… ,(ik-1,ik)是 D的弧,则弧的序列(i0,i1),(i1,i2),… ,(ik-1,ik)称为 D的一条途径,记为 W：(i0,i1),(i1,i2),…,(ik-1,ik).k称为途径的长度,记为 l(W).

关于 D(A)的有关概念也可以运用到矩阵 A=(aij)中,这样 A的途径 W定义为形式 ai0,i1ai1,i2,…,aik-1,ik,其中每一项都是非零的.类似地,可以定义 A的闭途径,简单圈的概念和长度及符号的概念.

设 S是定号有向图,若两条途径 W1和 W2有相同的起点,有相同的终点和相同的长度,但有不同的符号,则称 W1和 W2是 SSSD途径对.

设 a1,a2,… ,ak是正整数,定义 Froaenius集合

由 Schur引理可知,若 g.c.d(a1,a2,… ,an)=1,那么 S(a1,a2,… ,an)包含了所有充分大的正整数.

Froaenius数h(a1,a2,… ,an)定义是最小的正整数 h,使得任何整数 m≥h都有 m∈ S(a1,a2,… ,an)成立.显然由此定义有 h(a1,a2,… ,an)-1∉ S(a1,a2,… ,an).若 a,b是正整数,且 g.c.d(a,b)=1,则h(a,b)=(a-1)(b-1).

设 A是广义符号模式矩阵,若存在某个正整数 k,使得 Ak中含# 元素,则称 A是不可幂的.

设 A是 n阶广义符号模式矩阵,考虑序列 A1=A,A2,A3,因为仅有 4n2个不同的 n阶广义符号模式矩阵,所以在这个序列中一定有重复的.设 Al是第一个被重复的矩阵,记 Al=Al+p,其中 p＞0是最小的,则称 l为 A的基(记为 l(A)),p称为 A的周期(记为 p(A)).

为了方便起见,人们也对定号有向图定义相应的概念.设 S是 n阶定号有向图,则一定存在 n阶符号模式矩阵 A,使得其定号有向图 S(A)是 S.若 A是不可幂的,则 S是不可幂的.也将 A的基和周期的概念定义为 S的基和周期.

设 B是非负矩阵,若存在正整数 k,使得 Bk＞0,则称 B是本原矩阵.k的最小值称为 B的本原指数,记为 exp(B).设 A是广义符号模式,将 A的每个非零元素用+ 代替之后得到的非负矩阵记为|A|.若|A|是本原的,则称|A|是本原的,在此情形下定义 exp(A)=exp(|A|).

设有向图 D,若存在正整数 k,使得 D的任何两个顶点 x和 y(不必不同)在 D中都存在从顶点 x到顶点 y的长为 k的途径,则称 D为本原有向图,k的最小值称为 D的本原指数,记为 exp(D).众所周知,有向图 D是本原的,当且仅当 D是强连通的,且 D的所有圈长的最大公因式等于 1.由矩阵与图之间的关系,有矩阵 A是不可约的,当且仅当 D(A)是强连通的;A是本原矩阵,当且仅当是本原有向图.此时,exp(A)=exp(D).

设 R={l1,l2,… ,,lr}是本原有向图 D的圈长的集合,且 g.c.d(l1,l2,… ,lr)=1,x,y是 D的两个顶点,d(x,y)表示从顶点 x到顶点 y的距离,dR(x,y)表示至少接触长为 li(i=1,2,…,r)的圈一次的最短途径的长度.设 hR=h(l1,l2,… ,lr)是 Froaenius数,则

和

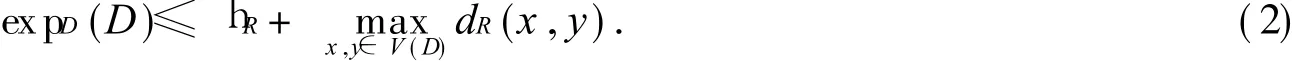
本文主要研究两类特殊本原不可幂的定号有向图(其基础有向图分别为 Ds,t和 Ds,t,q(分别见图 1和图 2)的基的界,其中：图 1中 s＞t和 2≤m≤s,图 2中 s,t,q中有两个相同.

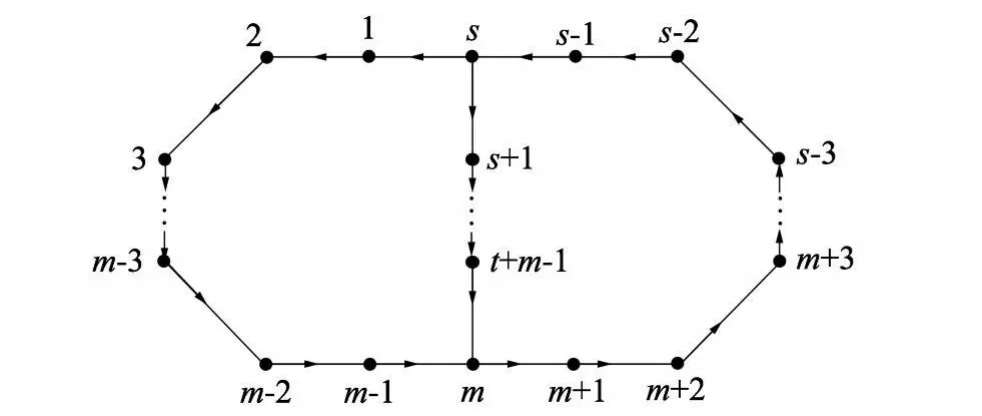
图1 有向图 Ds,t(s＞t)Fig.1 Digraph Ds,twhere s＞t

图2 有向图 Ds,t,qFig.2 Dig raph Ds,t,q

1 引 理

引理 1[2]若 S是本原的定号有向图,则 S是不可幂的,当且仅当 S包含的一对圈 C1和 C2(圈长分别为 p1和 p2)满足 p1是奇数,p2是偶数,且 sgn C2=-;或者 p1和 p2是奇数,且 sgn C1=-sgn C2.

满足引理 1的圈对 C1和 C2称为“异圈对”.若 C1和 C2是长分别为 p1和 p2的异圈对,则闭圈对 W1=p2C1和 W2=p1C2有相同的长度 p1,p2,但有不同的符号

引理 2[2]设 S是本原不可幂的定号有向图,则

1)存在整数 k,使得 S的任两个顶点 x和 y之间存在长为 k的 SSSD途径对;

2)若 S的任两个顶点 x和 y之间存在长为 k的 SSSD途径对,则 S的任两个顶点 x和 y之间存在长为 k+1的 SSSD途径对;

3)k的最小值是 S的基,即 l(S).

2 主要结论

定理 1 设 S是 n=t+m-1阶本原不可幂的定号有向图,其中 Ds,t(s＞t)(见图 1)是 S的基础有向图,则 l(S)=2st-t+(m-1).

证明 首先证明 S中从顶点 1到顶点 m-1不存在长为 k=2st-t+(m-2)的 SSSD途径对.设 P是从顶点 1到顶点 m-1的路,假设 W1和 W2是从顶点 1到顶点 m-1的长为 k的途径,显然每条途径Wi(i=1,2)是路 P和几个圈的“并”.因为 k＞m-2,所以每个“并”至少含一个圈 Cs.取 Wi=P+aiCi+biCs(bi≥ 1,ai≥ 0,i= 1,2), 有 k=l(Wi)=(m-2)+ tai+ sbi(bi≥ 1,ai≥ 0,i= 1,2), 故(b2-b1)s=(a1-a2)t.因为 s和 t的最大公因式为 1,所以记 a1-a2=sx,则有 b2-b1=tx,一定有 x=0.若 x≥ 1,则b2=b1+tx≥1+t,且 k=(m-2)+ta2+sb2=(m-2)+ta2+ [b2-(1+t)]s+(1+t)s.因为 S是本原的,且 Cs,Ct是 S中长分别为 s,t的仅有的两个圈,所以 h(s,t)-1=a2t+ [b2-(1+t)]s∈ S(s,t)与Froaenius数h(s,t)的定义矛盾.类似地,若 x≤-1,也得到一个矛盾,因此一定有 x=0,故 a1=a2,b1=b2且 sgn(W1)=sgn(W2),l(S)≥2st-t+(m-1).

证明对于 S的任意两个顶点 i和 j(1≤i,j≤n),在 S中都存在从顶点 i到顶点 j长不超过 2st-t+(m-1)的 SSSD途径对.先证明从顶点 s到顶点 m存在长为 st-(s-m)的 SSSD途径对.设 Q1和 Q2分别是 S中从顶点 s到顶点 m的长为 t+m-s和 m的路,设 Cs和 Ct分别是 S中长为 s和 t的圈.取W1=Q1+(s-1)Ct和 W2=Q2+(t-1)Cs,设 P′是 S中从顶点 m 到顶点 s的唯一的路,则 W1+P′=sCt和 W2+P′=tCs.因为 S是不可幂的,且 Cs和 Ct是 S中仅有的两个圈,所以由引理 1可知 Cs和 Ct一定是异圈对,则由式(3)可知 tCs和 sCt有不同的符号.因此 W1和 W2也有不同的符号,故 W1和 W2是从顶点 s到顶点 m 的长 rs,m=st-(s-m)的 SSSD途径对.设 P″是从顶点 i到顶点 s的长为 l=l(P″)的路,Q是从顶点 m到顶点 j的长为 expD(m)的途径,则 0≤l≤s-1.取 W3=P″+W1+Q和 W4=P″+W2+Q.显然 l(W3)=l(W4)=l+st-(s-m)+expD(m),且 W3和 W4是从顶点 i到顶点 j的 SSSD途径对.由式(1)可得

结合上述两个公式,可得 l(S)=2 st-t+(m-1).

定理 2 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中 Ds,t,q(见图 2)是 S的基础有向图.若 q=t,k≥2和 m≥k,则 1)若 S的长为 t的圈有不同的符号,则

2)若 S的长为 t的圈有相同的符号,则

和l(S)≤max{s-1,t+s-p-1}+2st-2s+k-t+ 1+max{s-1,t+m-1-k}.

证明 1)在图 2中 ,设 Q1=P(p→t+m)+P(t+m→k)+P(k→m)和 Q2=P(p→s)+P(s→s+1)+P(s+1→m)分别是S中从顶点 p到顶点 m的两条长为 t-(p-m)的路.若 S的长为 t的圈有不同的符号,则 sgn(Q1)=-sgn(Q2),即 Q1和 Q2是从顶点 p到顶点 m的 SSSD途径对.在 S中任取两个顶点 i和 j,设 T是从顶点 i到顶点 p的路,H是从顶点m到顶点 j的长为 expD(m)的途径.显然,W1=T+Q1+H和 W2=T+Q2+H是从顶点 i到顶点 j的 SSSD途径对.由定号有向图的基的定义,可得

2)若 S的长为 t的圈有相同的符号,则 sgn(Q1)=sgn(Q2).类似于定理 1的证明,若 s＜t,可以证明在 S中不存在从顶点 s+1到顶点 t+m-1长为 2st+t-2s+m-2的 SSSD途径对和不存在从顶点t+m到顶点 2t+m-2+k-p的长为 2st+t-s+k-p-2的 SSSD途径对,因此 l(S)≥max{2st+t-2s+m-1,2st+t-s+k-p-1}.若 s＞t,可以证明在 S中不存在从顶点 1到顶点 k-1的长为 2 st+k-t-1的 SSSD途径对,因此 l(S)≥2st+k-t-1.故

因为定号有向图 S是不可幂的,且 S的唯一的三个圈中有两个圈长为 t,一个圈长为 s,所以由定理1长为 t的每个圈与长为 s的圈形成了一个异圈对.所以由式(3)可知 tCs和 sCt有不同的符号.现在设P1=P(s→ 1)+p(1→ k) 和 P2=P(s→ t+m-1)+P(t+m-1→ m)+P(m→ p)+P(p→ t+m)+P(t+m→k)分别是从顶点s到顶点 k的长为 k和 2t+k-s的两条路.设 P=P(k→s)是从顶点 k到顶点 s的唯一路.令 W1=P1+(t-1)Cs和 W2=P2+(s-2)Ct.显然,W1和 W2是从顶点 s到顶点 k的途径,则W1+P=tCs和 W2+P=sCt,所以 W1和 W2是从顶点 s到顶点 k的长为 st-(s-k)的 SSSD途径对.

在定号有向图 S中任取两个顶点 i和 j,设 T是从顶点 i到顶点 s的最短路,H是从顶点 k到顶点j的长为 expD(k)的途径.显然,W3=T+W1+H和 W4=T+W2+H是从顶点 i到顶点 j的 SSSD途径对.由定号有向图的基的定义可得 l(S)≤max{s-1,t+s-p-1}+ 2st-2s+k-t+1+ max{s-1,t+m-1-k}.

类似于定理 2的证明,可以得到定理 3～定理 7.

定理 3 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中 Ds,t,q(见图 2)是 S的基础有向图.若 s=q和 m≥k,则 1)若 S的两个长为 s的圈有不同的符号,则

2)若 S的两个长为 s的圈有相同的符号,则

和

定理 4 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中 Ds,t,q(见图 2)是 S的基础有向图.若 s=t和 m≥k,则 1)若 S的两个长为 s的圈有不同的符号,则

2)若 S的两个长为 s的圈有相同的符号,则

和

定理 5 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中 Ds,t,q(见图 2)是 S的基础有向图.若 q=t和 m≤k,则 1)若 S的两个长为 t的圈有不同的符号,则

2)若 S的两个长为 t的圈有相同的符号,则

和

定理 6 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中 Ds,t,q(见图 2)是 S的基础有向图.若 s=q和 m≤k,则 1)若 S的两个长为 s的圈有不同的符号,则

2)若 S的两个长为 s的圈有相同的符号,则

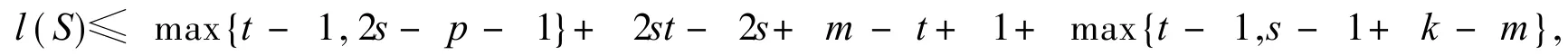
和

定理 7 设 S是 n=q+t+m-2+k-p阶本原不可幂的定号有向图,其中Ds,t,q(见图 2)是 S的基础有向图.若 s=t和 m≤k,则 1)若 S的两个长为 s的圈有不同的符号,则

l(S)≤max{s- 1,q-1+s-p}+m+sq-s-q+ 1+ max{s-1,q-1+k-m}.

2)若 S的两个长为 s的圈有相同的符号,则

和

[1]Li Z S,Hall F,Eschenbach C.On the period and base of a sign pattern matrix[J].Linear Algebra and Its Applications,1994,212/213：101-120.

[2]You L H,Shao J Y,Shan H Y.Bounds on the basis of irreducible generalized sign pattern atrices[J].Linear Algebra and Its Applications,2007,427：285-300.

[3]Liu B L,You L H.Bounds on the base of primitive nearly reducible sign pattern matrices[J].Linear Algebra and Its Applications,2006,418：863-881.

[4]Shao J Y.On the exponent of a primitive digraph[J].Linear Algebra and Its Applications,1985,64：21-31.