大跨斜腿刚构桥地震易损性分析

郑成龙， 龙晓鸿， 彭元诚， 姜 维， 廖 萍

(1.华中科技大学 a.土木工程与力学学院，b.控制结构湖北省重点实验室，湖北 武汉 430074;2.中交第二公路勘察设计研究院有限公司，湖北 武汉 430056;3.江苏泛亚联合建筑设计有限公司，江苏 无锡 214005)

桥梁是交通系统中的重要枢纽结构。由于其上重下轻的结构模式以及较大的高宽比，在地震作用下是易损坏的。公路桥梁的地震易损性通常可以用易损性曲线表示，这些曲线可以表示在不同强度地震作用下结构反应超过破坏阶段所定义的结构承载能力的条件概率。目前，国际上普遍采用的桥梁易损性分析方法主要有经验统计法和理论分析法。Basoz和 Kiremidjian［1］基于 Northridge地震后得到的桥梁损伤数据，进行桥梁分组后采用逻辑回归分析建立了经验易损性曲线。Hwang和Huo［2］提出了一种基于结构动力行为的数值模拟方法，建立了理论易损性曲线。但是目前的地震-桥梁系统非线性时程分析方法普遍采用墩的位移延性比作为评价桥梁损伤程度的指标(Hwang和刘晶波［3］)，根据梁智垚［4］的研究成果，对于大跨薄壁高墩连续钢构桥，位移延性比并不能准确地反映桥梁的破坏情况。本文根据地震作用下塑性铰的曲率延性指标进行抗震性能水准划分，给出了大跨斜腿刚构桥结构的易损性曲线。

1 工程概况与桥梁有限元模拟

1.1 工程概况

文本分析对象北盘江特大桥为预应力混凝土悬浇空腹(斜腿)式连续刚构桥(如图1所示)，主桥部分总长度为895 m，桥跨布置为82.5+220+290+220+82.5 m。上部结构采用连续变截面现浇混凝土箱梁，宽度为10.5 m，由钢筋混凝土桥墩支撑，主墩的高度分别为75 m、90 m、143 m、68 m，均采用双肢薄壁空心截面，其中中间两对桥墩设有空腹斜腿以提高根部刚度。桥台部分的支撑类型为简支。桥墩的纵向配筋主要采用直径32 mm，28 mm，20 mm的HRB335钢筋，横向箍筋为直径为16 mm和20 mm的HRB335钢筋。

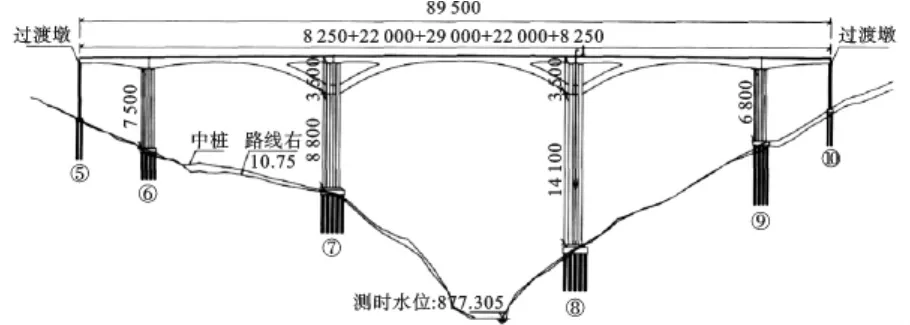
图1 主桥桥型布置图/cm

1.2 有限元模拟

图2 有限元模型三维整体视图

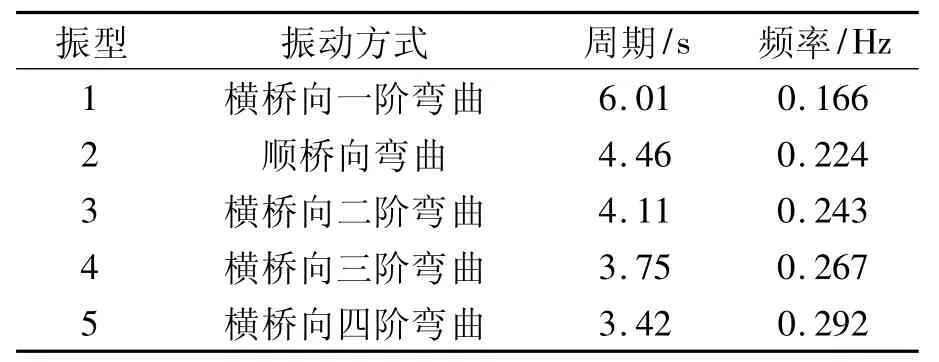
表1 模型的模态分析

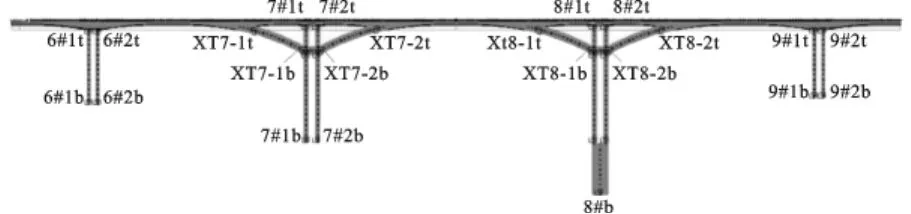
图3 塑性铰编号示意图

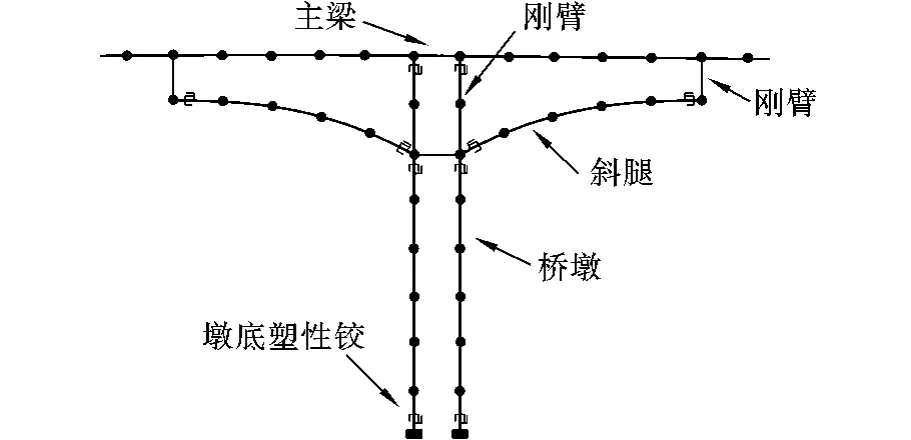
图4 单元连接示意图

1.3 塑性铰设置

桥墩的每种截面的弯矩-曲率曲线通过软件SECTION BUILDER计算得到，将钢筋和混凝土离散为纤维，假设纤维之间完全粘结，且满足平截面假定(如图5所示)。非线性特性由纤维的非线性应力-应变关系(材料非线性)，混凝土应力-应变关系常用Mander模型来模拟，并考虑到箍筋束缚对混凝土强度的加强，钢材用Ramberg-Osgood的钢筋本构模型模拟。截面的弯矩-曲率曲线通过对纤维单元的应力-应变关系积分而得。

对积分得到弯矩-曲率关系进行Caltrans［5］标准化，得到理想弹-塑性模型如图6所示，其中等效屈服曲率φy和等效屈服弯矩Mn为混凝土纤维达到极限受压应变ε=0.005时的对应值，其取值由坐标原点和首根钢筋屈服时的对应点外推得到:

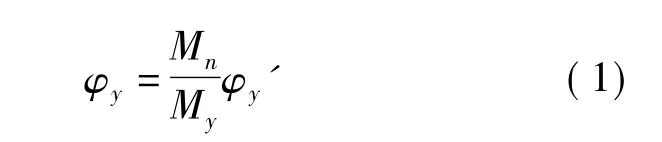
其中，My和φy'分别为截面第一根钢筋屈服时对应的弯矩和曲率。

塑性铰长度Lp采用Priesley的经验公式得到:

L为最大弯矩点到桥墩反弯点的距离，dbl为纵向钢筋的直径。

由此可以得到每个截面的弯矩-转角关系，其中转角 θ=Lpφy。

图5 钢筋混凝土截面纤维模型

图6 桥墩的弯矩-曲率曲线

2 结构易损性分析

本文选取了20条远场地震波，按照随机抽样对20条地震波地震加速度峰值(PGA)进行调整，PGA广泛分布于0.1g～1.4g，共计140个工况。

在SAP2000中定义非线性动力时程分析:首先，计算得到结构在恒载作用下的状态，然后对结构施加横桥向的地震加速度。因此在每个工况中，都考虑了恒载和地震的共同作用。时程计算的时间步长取0.02 s，共1000步，故地震波作用时间为20s。计算方法采用直接积分法，通过迭代得到结构每一子步的状态，每一次迭代的最大迭代次数为100次，如果迭代无法收敛，自动将步长细分，并再次进行计算。通过对140个样本进行非线性时程分析，得到了结构在地震作用下的响应。

社会的快速发展对教师队伍提出了更高的要求，教师为了适应这种需求变化必须不断学习以更新知识和技能，教师培训是提高教师综合素养的重要途径。教师是具有一定专业知识和实践经验的成人学习者，因此，教师培训必须借助成人学习理论，设计科学、有效的教师培训课程。[1]基于目标导向的“双主线”新任教师培训课程设计，依据培训目标设置基于工作绩效改进和专业素养提升两条主线的课程，更关注新任教师的可持续发展，既满足教师的实际需要，又超越当前需求，具有一定的引领性。

结构破坏准则的定义:结构的破坏主要是由于一些重要构件的破坏，由于北盘江大桥特有的结构形式，其重要构件主要为桥墩和斜腿，并且由数值模拟的结果可以看出桥墩的最大剪力小于其抗剪能力。因此，结构的破坏主要是由于桥墩受弯需求达到其延性能力后屈服造成。

2.1 地震需求分析

应用SAP2000对每一个地震-桥梁样本进行非线性时程分析。在此研究中，地震引起的结构反应是由墩的控制界面的相对曲率延性比μd来衡量，其中μd为截面屈服后的曲率与初始屈服曲率之比，即

墩底截面6#1b以及斜腿截面XT8-2b的140个地震-桥梁系统的分析结果分别绘于图7与图8中，以地面最大加速度PGA为变量。

以截面6#1b为例，通过对与地面最大加速度PGA为变量的结构反应数据的回归分析，可以得到结构反应为

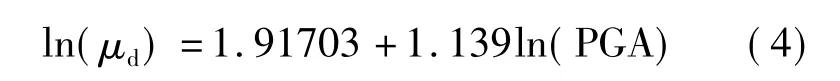
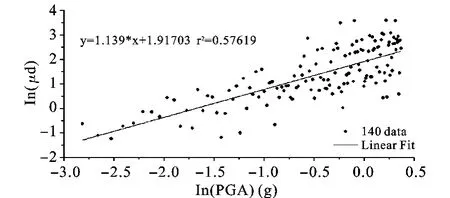
图7 墩底截面6#1b曲率延性比μd的回归分析

图8 斜腿截面XT8-2b曲率延性比μd的回归分析

在研究中，结构反应的概率函数用对数正态分布函数表示，此函数由结构反应均值和对数标准差βd来表示，即

2.2 桥梁破坏状态和结构承载能力概率

通过对结构反应的分析发现，在横桥向地震作用下，墩底各截面钢筋均能达到屈服，而墩顶截面在横桥向140个工况下均不会达到屈服状态，不会形成塑性铰。除墩底截面外，斜腿截面XT8-2b钢筋也会达到屈服。所有塑性铰截面中，截面6#1b为最危险截面，首先发生破坏。故以6#1b截面为标准形成桥梁地震易损性曲线。

根据Caltrans建议的桥梁抗震性能指标，从无破坏到完全破坏这一过程中，地震对桥梁的破坏有5种破坏状态。这5种破坏状态用桥墩控制截面的曲率延性比来表示，如表2所示。

表2 由曲率延性比定义的桥梁破坏状态

各状态之间对应的曲率延性界限，即为结构的承载能力μc。与结构反应分析相对应，结构的承载能力的概率函数μc也用对数正态分布函数来表示，该函数由两个参数来定义，即结构承载能力均值¯μd和对数标准差βc，

2.3 易损性曲线的形成

桥梁的破坏曲线表示在不同强度地震作用下结构反应超过破坏阶段所定义的结构承载能力的条件概率。结构反应μd超过结构承载力μc的概率可计算如下:

因为μc和μd都服从对数正态分布，所以特定阶段的失效概率Pf可由下式确定:

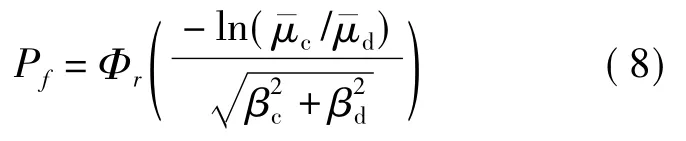
将式(4)代入式(6)可得用PGA表示的结构在特定阶段的失效概率如下:

根据 HAZUS99［6］，当易损性曲线以 PGA 为自变量时，取0.5。于是将对应于不同的PGA值时截面破坏的失效概率计算出来，得到结构的易损性曲线，如图9所示。图中横坐标表示地震动的大小，纵坐标表示地震作用下结构反应超越不同破坏状态的概率。

在获得结构的易损性曲线后，在给定地震作用下结构破坏概率的确定将变得很容易。根据《公路桥梁抗震设计细则》［7］各设防烈度在不同

图9 连续刚构桥的地震易损性曲线

相应于不同破坏状态时结构承载力均值由表1确定。地震影响时的 PGA，可以看出，地震烈度6度(0.05g)时，桥梁不会发生破坏;地震烈度7度(0.1g)时，桥梁发生轻微破坏的概率为0.2%;地震烈度8度(0.2g)时，桥梁发生轻微破坏的概率为11.2%，发生可修复破坏概率为0.5%。该地区基本地震烈度为6度，地震动峰值加速度为0.05g，满足设防要求。

3 结语

本文针对大跨斜腿钢构桥的薄壁高墩，采用地震作用下的塑性铰的曲率延性比作为抗震性能水准划分指标，通过对140个地震-桥梁样本的非线性时程分析建立了以PGA为变量的结构需求概率函数，给出了桥梁结构的易损性曲线，从而得到各级地震作用下的桥梁损伤评价。地震易损性分析可以预测结构在不同等级的地震作用下发生各级破坏的概率，对于结构的抗震设计、加固和维修决策具有重要的应用价值。

［1］Basoz Nesrin，Kiermidjian Anne S.Risk assessment of bridge and highway systems from the northridge earthquake［J］.Progress in Research and Practice，1997:65-79.

［2］Hwang H，Huo J R.Generation of hazard-consistent ground motions［J］.Soil Dynamics and Earthquake Engineering，1994，13(6):377-386.

［3］Hwang H，刘晶波.地震作用下钢筋混凝土桥梁结构易损性分析［J］.土木工程学报，2004，37(6):47-51.

［4］梁智垚.非规则高墩桥梁抗震设计理论研究［D］.上海:同济大学，2007.

［5］High Way Design Manual［S］.California Department of Transportation(Caltrans)，2009.

［6］HAZUS99 User’s Manual［S］.Washington，D C:Federal Emergency Management Agency，1999.

［7］JTG/T B02-01-2008，公路桥梁抗震设计细则［S］.

［8］Hwang H，Liu J B，Chiu Y H.Seismic Fragility Analysis of Highway Bridges［R］.Technical Report，Center for Earthquake Research and Information，University of Memphis，Menphis，TN.2000.

［9］Pan Y，Agrawal A K，Ghosn M.Seismic fragility of continuous steel highway bridges in New York state［J］.Journal of Bridge Engineering，2007，12(6):689-699.