曲轴随动磨削加工误差的模糊自学习补偿

沈南燕 方明伦 何永义 李 静 姚 俊

1.上海大学，上海，200072 2.上海电气集团股份有限公司，上海，200093

0 引言

曲轴是内燃机的关键零件，其加工质量对发动机的性能具有直接影响。采用非圆磨削技术取代使用专用夹具、调整偏心的传统方法加工曲轴，在一次装夹中即可完成主轴颈与连杆颈的磨削。在这种新方法中，曲轴绕主轴颈轴线回转，通过控制砂轮跟随连杆颈的运动而实现连杆颈的加工。虽然随动磨削具有加工工艺性及柔性好、效率高、成本低的特点，但其加工精度更易受到来自运动模型误差、工艺系统动态特性以及数控系统因素的影响。而误差补偿是提高随动磨削精度的最有效手段，将误差补偿量预先迭加到砂轮架的水平位移中，通过向数控系统提供附加脉冲修正量的方式消除曲轴连杆颈加工误差，是一种适应随动磨削特点的误差补偿策略。

针对曲轴形状复杂、刚性差，而且沿长度方向及圆周各方向上的刚性均不相等的特点，周志雄等[1]建立了刚度误差补偿模型，以消除曲轴受力发生的弹性变形对精度的影响，但是需要测量曲轴位于不同转角处的各个刚度系数。其给出的测定方法操作复杂，只适合实验研究，并不适用于实际加工。许第洪[2]认为曲轴连杆颈圆度误差的补偿量是连杆颈磨削点法向的综合加工误差在砂轮架水平方向的投影，并给出了误差补偿模型。文献[3]描述了连杆颈半径误差与砂轮架水平位移补偿量之间的几何关系。

随动磨削系统具有很强的非线性，而上述的误差补偿模型[1－3]都是对实际情况的线性近似，因此即使测量结果非常准确，模型的误差补偿效果也不一定令人满意。所以很难用一个数学模型来精确描述连杆颈加工误差的规律。

由于神经网络具有非线性适应性信息处理能力，吴钢华等[4]采用RBF网络，根据实际加工结果和工艺参数，建立了连杆颈随动磨削误差预报模型，为其误差补偿提供了依据。另外，Tian等[5]在可转位刀片的随动磨削中设计了基于自学习控制器的智能加工误差补偿系统，并给出相应的尺寸误差在线智能补偿算法。

本文结合以往补偿经验及其发展趋势，提出了具有自学习功能的曲轴随动磨削加工误差模糊推理补偿方法，在加速收敛的同时，还能克服偶然因素或非线性因素对补偿效果的不良影响。

1 曲轴随动磨削原理和加工误差分析

如图1所示，图中OW为连杆颈中心，OS为砂轮中心。在随动磨削中，曲轴绕主轴颈轴线C轴回转，通过控制砂轮跟随连杆颈，沿X轴往复运动，实现连杆颈的加工，其运动模型为

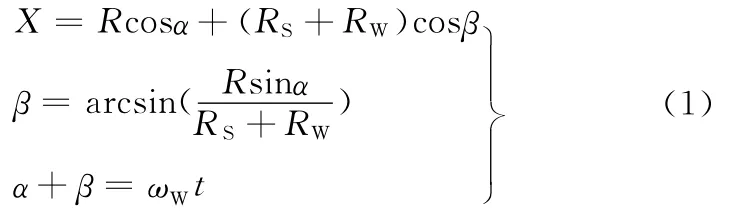
式中，R为曲轴的曲柄半径；RW为连杆颈半径；α为O OW与OOS的夹角；β为OSOW与OOS的夹角；X为砂轮中心距连杆颈回转中心的距离；ωW为磨削点绕沿连杆颈中心OW匀速转动的角速度；t为时间变量。

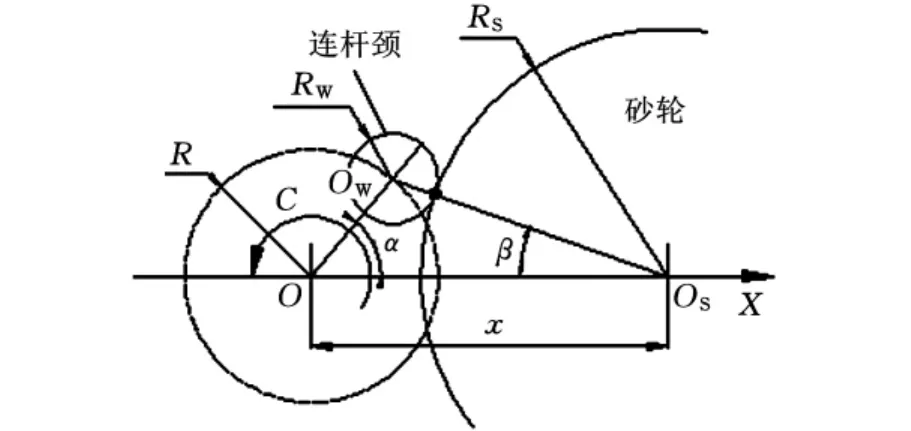
图1 曲轴随动磨削参数描述

作为一种新的磨削方法，它与传统磨削方式的误差来源不尽相同。首先，曲轴非圆磨削过程中理想情况是必须保证磨除率恒定，即工件被磨削的深度恒定，这样才能保证连杆颈的尺寸精度与圆度。但是工件速度与砂轮速度不断变化引起磨削力大小变化，加上X轴往复运动过程中的加速度变化以及砂轮磨损等引起的变化，很难控制磨削时的当量磨削厚度、磨除率保持恒定。另外，曲轴形状复杂、刚性差，而且沿长度方向及圆周各方向的刚性均不相等，将导致在连杆颈圆周各方向产生大小不一的弹性变形，对工件的圆度有较大影响。而且，与外圆磨削中砂轮半径的变化或是伺服系统滞后误差只会影响工件的尺寸精度的情况不同，在曲轴非圆磨削中砂轮半径变化或伺服系统滞后误差会对曲轴各个转角位置上连杆颈尺寸造成不同的影响，最终不仅影响工件的尺寸精度，还将导致连杆颈的圆度误差。

2 模糊自学习误差补偿系统结构和原理

本文提出的基于模糊自学习的曲轴随动磨削加工误差补偿系统如图2所示。在曲轴随动磨削系统中，连杆颈半径误差检测装置和二维模糊自学习控制器构成了连杆颈加工误差的补偿控制环节。此模糊自学习加工误差补偿环节由比较器、数据库、模糊推理机、规则库、学习机组成。由自学习模糊推理得到：第k＋1个循环中X轴位移补偿值，并在第k＋1个磨削循环中对连杆颈轮廓的加工误差进行补偿。

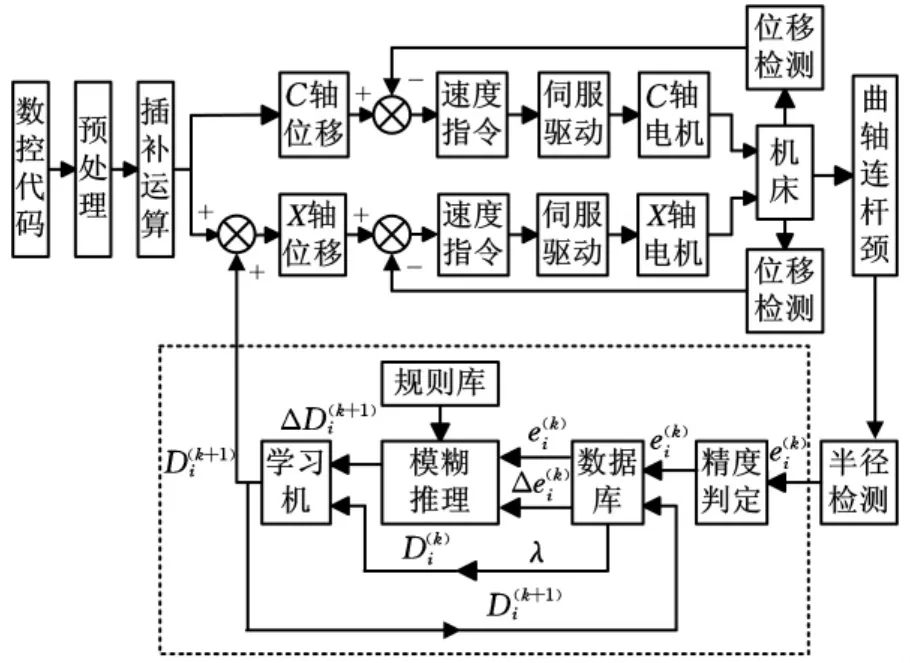
图2 模糊自学习加工误差补偿系统框图

2.1 精度判定

第k个磨削循环后，由连杆颈半径测量装置获取圆周上各点半径误差值

曲轴随动磨削循环以C轴回转一周的时间为周期，因此连杆颈加工误差补偿也以此为周期，即根据第k个磨削循环后连杆颈轮廓上各点i的半径误差测量值，比较器将依据以下两个性能指标判断补偿精度：

2.2 学习机

常规的模糊推理系统由专家经验建立模糊规则，自学习能力不强。为此本文采用一种简单有效地自学习算法[6]（式（2）），综合模糊推理结果和以往补偿量获取下一磨削循环的最终补偿值。

式中，Dki为第k个磨削循环中点i处的补偿值；ΔD（k＋1）i为模糊推理得到的第k＋1个磨削循环中点i处的补偿初值；G为自学习增益，在区间[0，1]内根据误差值调整，当误差变大时可提高G值，以加强学习力度，加快收敛速度。

3 加工误差补偿量的模糊推理系统设计

模糊控制的实现需要经过输入量模糊化、模糊推理以及输出量去模糊化三个环节。模糊控制器设计参数主要有：输入输出变量的比例变换因子、各输入输出变量模糊子集的隶属度函数以及模糊控制规则等[7]。

3.1 模糊化

模糊化运算是将观测到的连杆颈半径误差及其变化量映射为输入论域上的模糊集合。在模糊化前，首先要对两个输入量进行尺度变换，将其变换到相应的论域范围。本文采用文献[8]中的线性变换方法，即若实际的半径误差输入量为ei∈

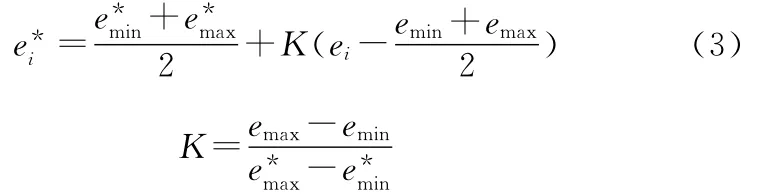
式中，K为比例因子。

在对误差变化量Δei进行尺度变化前，为了减小噪声的影响，本文采用下式对Δei进行滤波[7]：

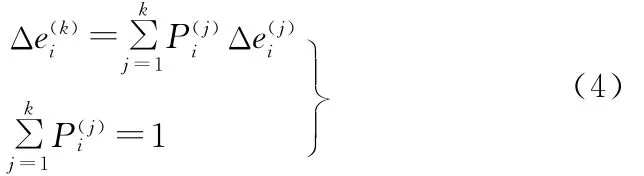
选用图3所示的三角形隶属度函数对模糊输入、输出空间进行模糊分割。取输入输出的论域∪ 均为｛－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6｝。

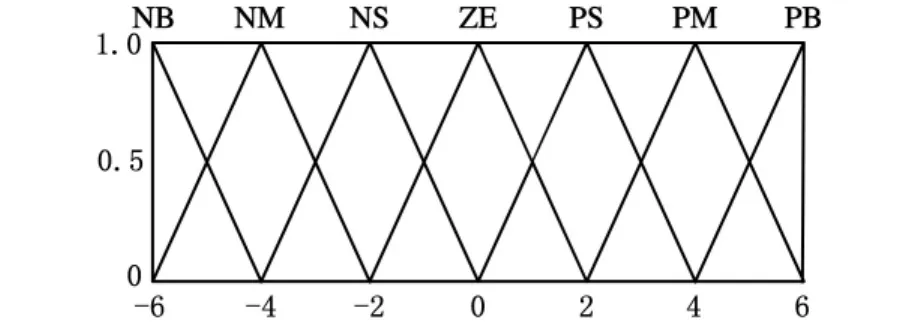
图3 三角形隶属度函数分布图

3.2 模糊推理

模糊推理过程是基于模糊逻辑中的蕴含关系及推理规则来进行的，其中推理规则的建立是设计、实现模糊控制的核心问题。本文基于专家经验和控制工程知识建立的推理规则如表1所示。

表1 模糊推理规则表

表1中，P表示正数；N表示负数；ZO表示零；B、M、S分别表示数值绝对值的大、中、小；E、ΔE和ΔDF分别为半径误差、半径误差变化量和补偿量初值（上标F表示此处的补偿量初值是模糊量）。其主要补偿策略如下：

（1）EΔE＞0：表明误差方向与前一次相反（过补偿）或者误差方向未变、但数值增大的情况，这时的补偿策略是在误差的反方向大大提高补偿量初值ΔDF，且其值随误差增大而增大。

（2）EΔE＜0且ΔE≪E：表明误差值较前一次有所减少，但是仍然较大，且收敛速度较慢，这时的补偿策略是在误差的反方向保持适当补偿量初值ΔDF。

（3）EΔE＜0且ΔE≫E：表明误差值已经很小，且收敛速度很快，这时若继续在误差的反向施加补偿量初值ΔDF，很可能出现过补偿，因此在误差的同向给予少量的补偿以防止这种趋势。

（4）EΔE＜0且｜ΔE｜≫0且｜E｜≫0，这种情况很少发生，因此均置为0（ZE）。

3.3 去模糊化

通过模糊推理得到的是模糊量，而补偿时需要的补偿量的精确值，因此需要进行去模糊化计算。本文采用重心法[8]，即取输出模糊量ΔDFj的隶属度值μ（ΔDFj）的加权平均值为其精确值，表达式如下：

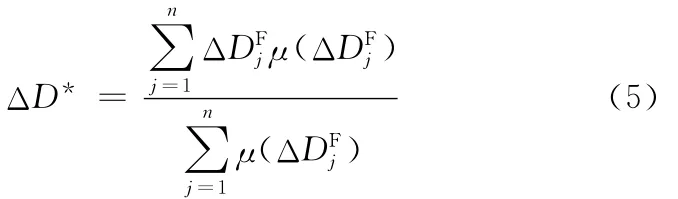
取得精确值ΔD＊之后，再经尺度变换就可得到实际的补偿量初值ΔD。

4 基于MATLAB的模糊推理系统的实现

MATLAB模糊逻辑工具箱提供了建立和测试模糊逻辑系统的一整套函数；同时还提供了三个交互式系统设计工具：模糊推理系统编辑器、隶属度函数编辑器、模糊推理规则编辑器以及两个图形化浏览器：模糊推理过程游览器和输入输出特性曲面游览器[7－8]。

本文首先利用上述三个编辑器，建立模糊逻辑系统的整体框架，定义如图3所示的语言变量的隶属度函数，根据表1添加了模糊规则，并将设计好的模糊逻辑系统文件CrankErrCom.fis导出至硬盘。使用输入输出特性曲面游览器可以得到该模糊系统的输入输出特性曲面，如图4所示。

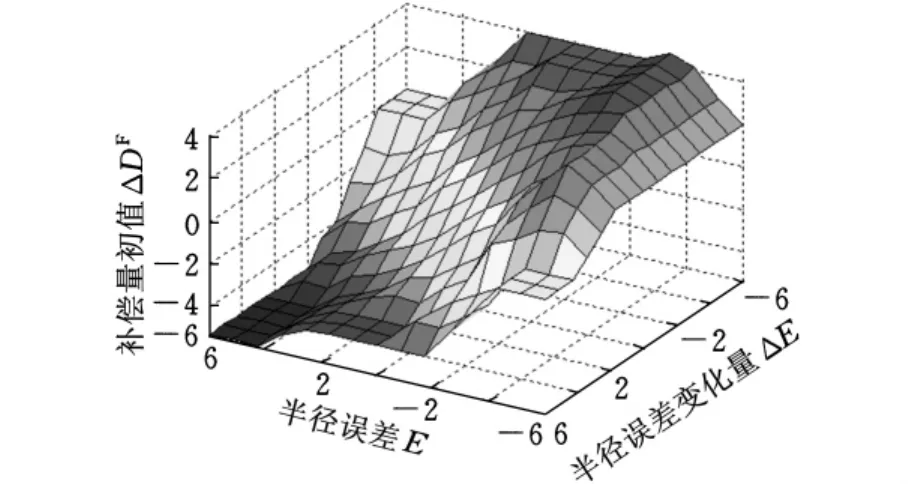
图4 模糊逻辑系统输入输出特性曲面

本文利用MATLAB提供的组件对象模型编译工具，将编制成M函数文件的补偿量模糊推理输出程序fuzzycomoutput.m（表2）自动转变为以动态链接库形式存在的、独立的进程内组件对象模型（component object model，COM）组件，供曲轴随动磨削控制软件调用。

5 加工误差补偿实验

加工误差补偿实验在上海机床厂制造的H405BF数控随动曲轴磨床上进行。该机床采用西门子SINUMERIK 840D开放式数控系统，模糊推理过程作为曲轴随动磨削控制软件的一部分在其人机交互界面（man machine communication，MMC）中完成，而补偿值则通过总线传输到数控系统的内存中，在下一磨削循环中供调用。

实验对象为一六缸曲轴，主要工艺参数如下：曲柄半径RW＝37.5mm；偏心距R＝67.5mm；砂轮半径RS＝299.988mm；砂轮线速度v＝45m／s；磨削速度n＝8r／min；进给量a＝2μm／r。

连杆颈圆度误差补偿效果比较如图5所示。图5a是第一个磨削循环中未经补偿时，连杆颈半径误差随转角变化的曲线，其中，半径误差最小值为－0.0124mm、最大值为0.0141mm，圆度误差为0.0265mm。图5b是第二个磨削循环后半径误差变化的曲线，在该循环中使用模糊推理得到的综合补偿值ΔDi对砂轮架的理论位移进行了补偿，连杆颈圆度误差缩小至0.0105mm；图5c为三个磨削循环后，经过两次补偿得到的曲线，图5c中最小半径误差为－0.0015mm、最大值为0.0051mm，圆度误差为0.0066mm。此时，误差补偿系统的两个性能指标均小于期望值，补偿环节停止工作，连杆颈的磨削结束。

表2 补偿量模糊推理输出程序

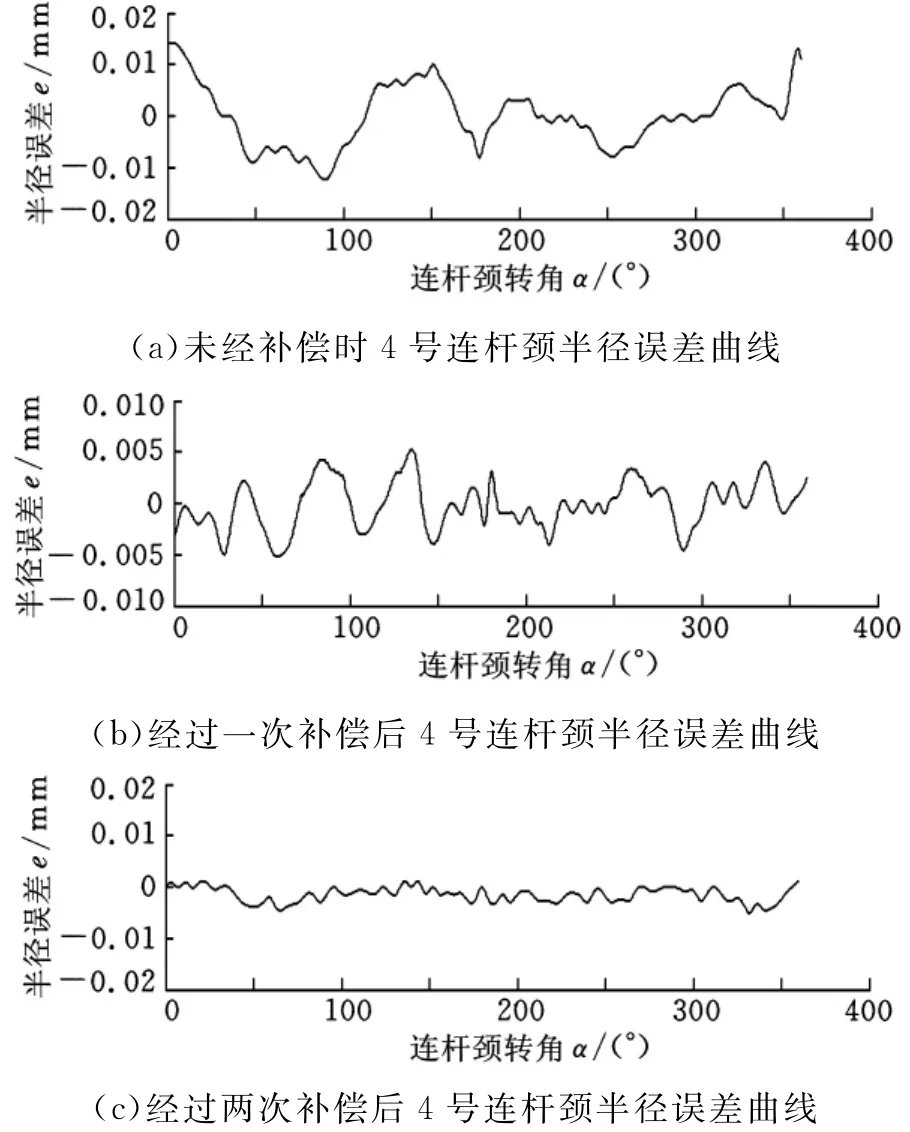
图5 连杆颈圆度误差补偿效果比较

6 结语

实验结果表明本文提出的加工误差模糊自学习补偿方法适应于曲轴随动磨削，能够在几个磨削循环内将连杆颈的圆度误差、半径误差缩小到期望值内，具有较高的补偿效率和适应性。

[1]周志雄，罗红平，许第洪，等.切点跟踪磨削法中工件的刚度误差分析及其补偿[J].机械工程学报，2003，39（6）：98-101.

[2]许第洪.切点跟踪磨削法核心技术的研究[D].长沙：湖南大学，2005.

[3]吴钢华.曲轴非圆磨削轨迹控制关键技术研究[D].上海：上海大学，2006.

[4]吴钢华，沈南燕，方明伦.曲轴非圆磨削运动中动态误差及补偿[J].机械工程学报，2009，45（1）：101－105.

[5]Tian Xincheng，Huissoon J P，Xu Qing，et al.Dimensional Error Analysis and Its Intelligent Pre－compensation in CNC Grinding[J].International Journal of Advanced Manufacturing Technology，2008，36：28－33.

[6]张秋菊，赵一丁，毛军红，等.模糊自学习误差补偿方法及其在位置误差补偿中的应用[J].西安交通大学学报，1995，29（2）：67－71.

[7]李国勇.智能控制及其 MATLAB实现[M].北京：电子工业出版社，2005.

[8]林献坤，李爱平，张为民.应用基于学习的模糊逻辑智能选择铣削加工参数[J].中国机械工程，2007，18（9）：1076－1080.