基于响应面法的函数敏感性快速分析

孙建勋 潘 雷 谷良贤

西北工业大学，西安，710072

0 引言

敏感性分析是多学科设计优化的重要工具，可分为一维函数和多维函数的敏感性分析。目前，常用的一维敏感性分析方法有差商法、复步长法、逆波兰表示法、符号分析法和自动微分法等5种[1]，而多维敏感性分析则有敏感性矩阵法、滞后耦合伴随法等[2]。这些方法在进行函数敏感性计算时都需要进行大量函数值计算，从而使得敏感性分析的代价极其巨大。研究表明，在一次优化循环中，有70%以上的计算费用用于函数敏感性分析[3]。因而，降低敏感性分析费用，寻找快速有效的敏感性分析方法一直是敏感性分析的一个重要研究方向[4]。

响应面法是一种常用的近似技术，它通过对函数的一系列已知点进行拟合从而推测函数的变化趋势[5]。本文结合响应面法特点，提出一种基于响应面法的函数敏感性分析方法。该方法计算简单，适于快速敏感性分析。在优化过程中引入该方法能够减少目标函数计算次数，加快优化收敛过程，减少优化费用。

1 多项式响应面与函数敏感性的关系

基于多项式的响应面法通常采用高阶多项式，其中最常用的是二阶响应面，也称二次响应面。用η表示二次响应面模型的响应量，则具有n个变量的二次响应面函数为

当给定一组已知数据时，则可利用最小二乘法对式（1）进行求解。

将待拟合函数y＝f（X）在X0点展开，得

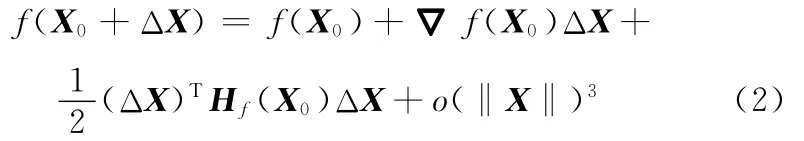
其中，▽f（X0）为函数f在X0点的梯度，即敏感性；Hf（X0）为函数f在X0点的Hessian矩阵；o（‖X‖3）表示余项为三阶无穷小量。对比式（1）与式（2）可知，多项式响应面（response surface method，RSM）近似的主要思想仍为Taylor展开的思想，响应面的系数从某种程度上近似反映了原函数的一阶梯度与二阶梯度。

实际问题中，函数往往以隐函数的形式表示，因而有必要研究隐函数情况下的敏感性与响应面系数的关系。考虑最一般的情况，状态变量u为该学科设计变量Xd、耦合设计变量Xs以及耦合状态变量Ys的函数，即u＝f（Xd，Xs，Ys），对应的响应面可描述为

式中，β为待定系数。

对式（3）求全微分：

则在任一点（Xd，Xs，Ys）处，根据全微分关系du＝▽fdx可知

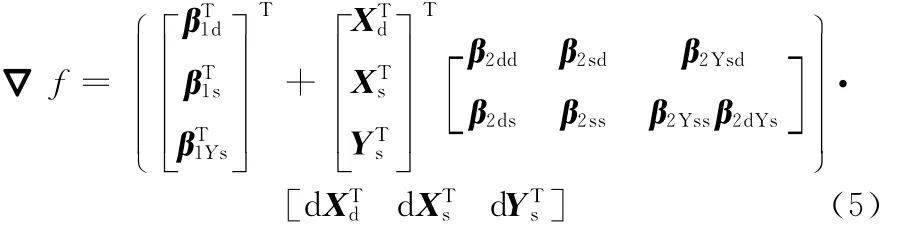
式（5）即为响应面法计算任一点梯度的近似计算公式。

需要注意的是，在进行系统全局敏感性计算时，耦合状态变量Ys的微分dYTs需通过各个学科的响应面进行求解。分别按上述方法对每个子系统进行处理，并假定一个系统只含有一个状态变量，则n个子系统中共含有n个dYs，构成一个n元线性方程组。解此方程组则可求得各学科的敏感性。

显然，这种基于响应面法的敏感性分析方法的优点在于计算简单，只需要根据响应面的系数求解若干个由式（5）组成的线性方程组，避免了大量调用原函数，尤其是对于存在状态变量耦合的系统，可以避免状态变量的迭代求解过程。因而该方法简单快捷，可用于快速敏感性分析。

2 敏感性近似能力分析

采用一个三元显函数算例（式（6））来测试基于RSM的函数敏感性计算能力：

图1为部分参数固定情况下的函数图像，由图1可知，该函数的敏感性变化范围比较大，变化情况多样，适于敏感性计算性能测试。

图1 x2、x3 固定时测试函数y（x1）图像

采用二阶分块响应面近似方法[6]，首先检验该RSM曲面拟合精度。在设计空间中按照均匀试验设计方法选取45个试验点，其中x1维5个测试点，其他两维都是3个测试点。图2为测试结果，其中，大部分计算结果都在解析解附近，近似结果与解析结果的最大误差不超过5%。因而，采用分块RSM有效地拟合了原设计空间，可以用于梯度近似计算。

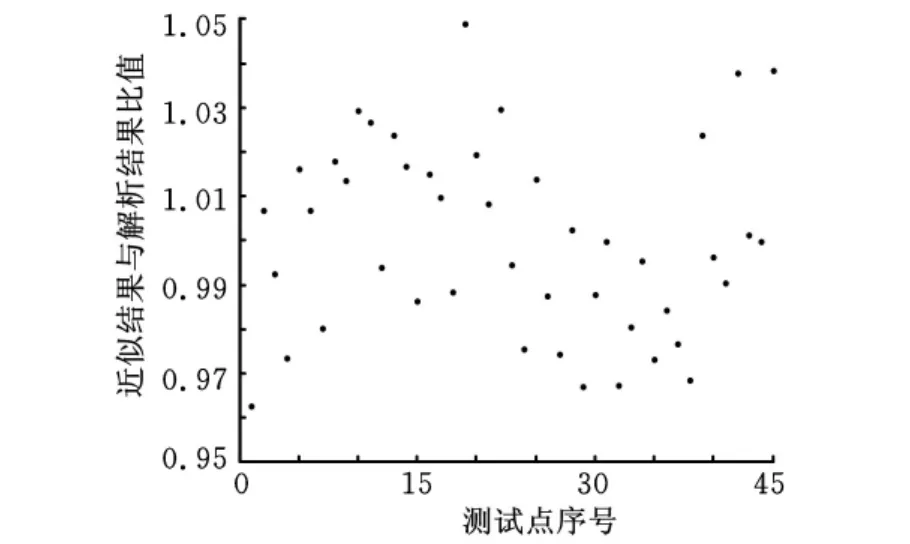
图2 RSM近似性能图像

在整个设计空间内按照均匀试验设计的方法选取112个测试点，其中x1维7个测试点，其他两维都是4个测试点。图3给出了RSM在测试点处计算得到的近似敏感性值和解析值的比值。表1给出了图3部分测试点的解析结果、近似结果和计算误差。

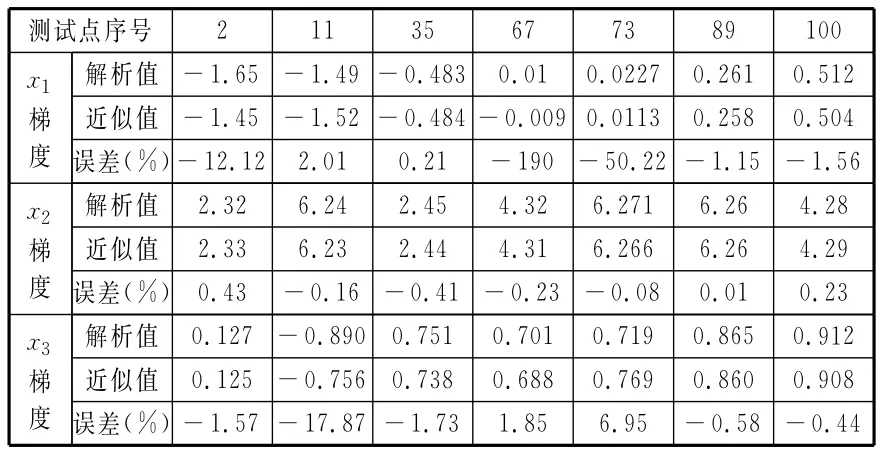
表1 图3中的典型点敏感性结果

图3 RSM梯度近似结果和解析值比值

图3表明，RSM方法近似梯度计算结果整体性能较好，但存在部分点近似结果误差较大。结合表1可以看出，当解析梯度数值较大时，RSM方法近似梯度计算得到的结果和解析结果误差不大，如点35、点89处的结果。而当解析结果接近0时，即当原函数接近其极点时，RSM方法计算结果和原函数的解析结果会有较大的相对误差，甚至出现符号反向的情况，但此时绝对误差却很小，如点67处的x1维梯度值，解析结果为0.01，近似结果为－0.009，两者相对误差高达190%，而绝对误差小于0.02，不及该点其他维梯度绝对误差的1%。同样，点73处x1维梯度值的解析结果和近似结果有着较大的相对误差，但两者的绝对误差则很小，不足该点处其他维梯度绝对误差的0.5%。与其他维敏感性相比，该维的计算误差可以忽略。

图4给出了在x2、x3维固定时，RSM方法沿x1维对3个自变量的梯度计算结果与解析结果的比值变化图。x2、x3维的近似梯度计算结果比较满意，除x3维个别点误差在15%附近外，其余结果误差都在10%以内。对该结果进行分析可得出与图3同样的结论。

图4 x1维近似梯度和解析梯度的比值

3 基于响应面近似的函数优化

敏感性分析的一个重要用途是用于优化设计，下面用一个实例来检验基于响应面近似的敏感性快速分析策略的性能。该算例用于计算在两冲量作用下共面椭圆轨道转移问题，如图5所示。选取优化变量为转移轨道的近地点幅角ω、半长轴a和偏心率e，优化目标为最小化轨道转移的能量需求，模型表述为

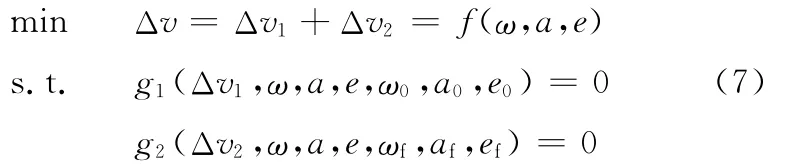
式中，下标0表示初始轨道参数；下标f表示终端轨道参数。

图5 两冲量共面椭圆轨道转移

在上述条件下每次轨道转移需要的冲量大小计算过程见文献[7]。

对问题归一化处理，设初始轨道与目标轨道的半长轴长度均为0.5、近地点幅角分别为0、－π／6，偏心率均为0.1。选用序列二次规划法进行优化计算，并分别采用有限差分法和基于RSM的敏感性快速计算法获得优化过程需要的梯度信息，当函数敏感性小于0.1时采用有限差分法获得敏感性。优化得到的最优转移轨道参数为（a，w，e）＝ （5.438，0.499，0.001），此时需要的转移能量大小为0.176。

图6所示为两种方法的收敛过程，该图表明，两种方法中目标函数的收敛过程很接近，这表明基于RSM的敏感性分析法可有效用于优化过程。

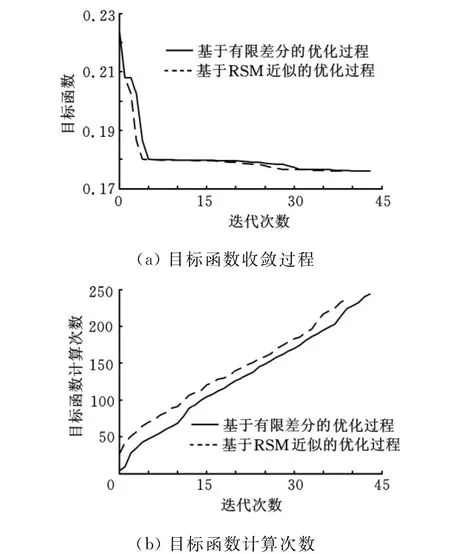
图6 优化收敛过程

由图6b可知，基于RSM的敏感性近似优化过程的目标函数计算次数要少于基于有限差分优化过程的目标函数计算次数。主要原因是，响应面法在迭代开始大量计算目标函数，生成响应面。在迭代后期采用快速敏感性分析法，不需要计算目标函数。有限差分法则自始至终都需要进行目标函数计算。基于RSM近似的优化过程总共循环了39次，目标函数计算次数为237；基于有限差分的优化过程总共循环了44次，目标函数计算次数为244。总的来看，采用RSM敏感性近似计算的优化过程目标函数计算次数要少。

4 结论

（1）RSM在大部分情况下能够有效近似目标曲面的敏感性。但在目标曲面极点附近，即目标曲面的敏感性较小时，RSM敏感性近似结果较差。

（2）基于RSM的敏感性计算方法能够有效用于优化过程，减少优化过程的目标函数计算次数，加快收敛过程，并得到理想结果。

（3）基于RSM方法的函数敏感性分析计算简单，在非极点附近计算精度较高，是一个良好的快速敏感性分析工具。

[1]蔡毅，邢岩，胡丹.敏感性分析综述[J].北京师范大学学报（自然科学版），2008，44（1）：9-16.

[2]钟毅芳，陈柏鸿，王周宏.多学科综合优化设计原理与方法[M].武汉：华中科技大学出版社，2006.

[3]Edmond P，Pelletier D，Etienne S.A Sensitivity E－quation Method for Compressible Subsonic Laminar Airfoil Flows[C]／／23rd AIAA Applied Aerodynamics Conference.Ontario，Canada，2005：AIAA 2005－4601.

[4]Martins J，Kroo I，Alonso J.An Automated Method for Sensitivity Analysis Using Complex Variables[C]／／38th Aerospace Sciences Meeting and Exhibit.Reno，NV，2000：AIAA－2000－0689.

[5]余大胜，康海贵.响应面法计算结构可靠度的回顾[J].工业建筑，2006，36：238－242.

[6]潘雷，谷良贤.分块响应面法研究[J].计算机工程与应用，2009，45（19）：37－40.

[7]杨嘉墀.航天器轨道动力学与控制[M].北京：宇航出版社，2001.