面向自然二次曲面的喷涂机器人喷枪轨迹优化

曾 勇 龚 俊

兰州理工大学数字制造技术与应用省部共建教育部重点实验室，兰州，730050

0 引言

喷涂机器人喷枪轨迹优化是喷涂机器人离线编程法的关键技术，国内外学者围绕着此问题展开了深入的研究。目前，面向平面的喷涂轨迹优化得到了一定程度的研究，并得到了试验验证[1－3]。自由曲面中的类自然二次曲面作为机械工程中出现较多的曲面类型，越来越受到研究者的关注，诸如汽车车门的类圆柱面、汽车保险杠拐角处的类圆锥面和导弹弹头的类球面等。文献[4-6]给出了自由曲面上喷枪空间路径的自动生成方法，但没有给出轨迹的优化方案，无法达到较高的涂层均匀性要求。文献[7]只针对喷涂机器人关节空间的最优轨迹规划问题进行了研究，采用遗传算法对问题进行求解，但没有考虑到自由曲面上的喷枪轨迹优化问题。文献[8]针对凹凸结构曲面，采用微分几何的面积放大定理推导出自由曲面上的漆膜累积速率二次函数，并采用轨迹优化的方法对表面有凹凸结构曲面的涂层厚度差进行补偿，仿真试验表明该方法能有效地提高涂层的均匀性，但还未达到较高的涂层均匀性标准。文献[9]给出了简单自由曲面的喷枪轨迹优化方法，但没有考虑到大型自由曲面的分片问题，无法适用于大型零件的喷涂要求。文献[10－11]针对大型复杂曲面，对复杂曲面的分片及喷枪路径模式、路径规划方式进行了详细的分析，并建立了复杂曲面分片后每一片上的喷枪轨迹优化函数，讨论了面片交界处的涂层厚度均匀性问题，证明出当两面片的喷枪轨迹相对于交界线平行时（parallel－parallel，PA－PA），涂层厚度均匀性最佳的结论，但他们的讨论是建立在平面分片原则的基础上进行的，该理论只适用于曲率较小曲面，如遇到曲率较大的曲面时，会出现分片数较多及涂层均匀性欠佳的问题。文献[12]针对提高直纹曲面喷涂时的涂层均匀性问题，第一次引入了喷枪3D模型，运用该模型讨论喷枪轨迹优化目标函数的建立，仿真试验表明喷枪3D模型的运用可有效提高大曲率曲面上的涂层均匀性。虽然目前针对复杂自由曲面的喷涂轨迹优化研究取得了一定的进展，但针对自然二次曲面的喷涂轨迹优化研究还未成熟，究其原因是，当作为喷涂对象的复杂自由曲面中出现曲率较大的类自然二次曲面时，传统的处理方法是将曲面进行离散造型处理，形成若干个近似平面片，具体针对每个平面片进行喷涂轨迹优化，有时为了适应新的喷涂作业标准，不得不增加分片的数量来逼近平面，这样却降低了喷枪轨迹规划的效率。

本文根据试验数据建立的喷枪2D模型，运用几何关系推导得到自然二次曲面上的喷枪3D模型；由于机械工程中类自然二次曲面运用得较多，因此将复杂自由曲面中曲率较大的类自然二次曲面拟合成自然二次曲面；在每个自然二次曲面上建立喷枪轨迹优化目标函数，并以某汽车后保险杠为例，给出了圆柱面和圆锥面与平面交界处的涂层厚度计算方法和相关参数优化方法；最后通过仿真试验验证本文所述方法的有效性。

1 喷枪数学模型的建立

1.1 平面上喷枪的2D模型

喷枪位置和姿态在固定的笛卡尔坐标系OXYZ中可定义为一个六维的时间矢量函数：Py（t），Pz（t））T，表示喷枪相对于固定笛卡儿坐标系OXYZ的位置；表示喷枪相对于OXYZ轴的角度。

根据喷涂特点，从喷枪口形成的喷炬的截面一般是圆形的，且涂层厚度在各向同性，设喷枪喷出的喷炬形状是圆锥体，其平面上的喷炬模型如图1a所示。图1a中，φ为圆锥张角，h为喷枪到平面的距离，R为平面上的喷涂半径，r为平面上一点Q离喷枪中心投影点的距离，θ为Q点和喷枪的连线与喷枪中轴线的夹角。平面上涂层累积速率为G，G ＝f（r，h）。实际应用中，喷枪离工件表面的距离一般保持不变，则G只与r有关：G ＝f（r）。此时G与r的函数图形可以近似看成抛物线[13]，如图1b所示。试验中采用Goodman方法测取平面上采样点的涂层累积速率数据后[14]，即可得到G的表达式，其中，A为常数。

图1 喷炬模型与涂层生长速率函数

1.2 自然二次曲面上喷枪的3D模型

自然二次曲面包括圆锥面、圆柱面和球面，平面可认为是退化了的自然二次全面。在曲面上建立较为精确的喷枪3D模型，可有效地提高曲面上的涂层厚度计算精度。

由于在喷涂过程中，随着喷枪与工件表面距离的变化，即不同截面，涂料的生长速率函数不会发生变化[15]，它是喷炬的固有特性，根据自由曲面上涂层生长速率模型建立的方法[16]，喷枪在圆弧面（凸凹）上的涂层生长速率模型如图2所示，平面P1为参考平面，且与圆弧面相切，平面P2为过点S且与P1平行的平面，θS为喷枪和点S的连线与喷枪轴线之间的夹角，h为喷枪到参考平面P1的垂直距离，hS为喷枪到平面P2的垂直距离，rS为点S到喷枪轴线的距离，λS为圆弧圆心和点S的连线与喷枪轴线之间的夹角，以圆弧圆心为坐标原点，喷枪轴线方向为Y向，建立空间直角坐标系，假设喷枪喷到参考平面上和圆弧面上的涂料量相等，喷枪在参考平面P1上喷出的一块很小的圆形面为c1，c1在平面P2上的投影面为c2，则两圆形面的面积关系为

式中，Sc1、Sc2分别为c1、c2的面积。

图2 圆弧面上的涂层生长模型

设c1上的涂层厚度为q1，则c2上的涂层厚度为

设圆形面c3与喷枪喷射方向垂直且与c2在同一圆锥喷射张角下，如图3a所示，则c2与c3的夹角即为θS；再设c3的法向量与圆弧面上过点S的一小块圆形面c4的法向量n的夹角为γS，如图3b所示，则c3和c4的涂层厚度分别为

图3 不同夹角圆形面之间关系示意图

最后，结合式（1）～ 式（4）和圆弧面（凸凹）的几何特征，半径为ρ的圆弧面上涂层生长速率可以表示为

由于圆柱面和圆锥面均属于柱面类型，在半径为R的喷涂范围内，圆锥面上的喷枪模型可由圆柱面上的喷枪模型近似表示。由于圆柱面各向并不同性，喷枪在圆柱面上形成的涂层覆盖范围在OXZ面上的投影域为一椭圆形区域，而由于球面的各向同性，喷枪在球面上形成的涂层覆盖范围在OXZ面上的投影域则为一圆形区域。

2 曲面喷涂分片规划

针对类自然二次曲面的喷涂轨迹优化问题，将类自然二次曲面分片规划成自然二次曲面的组合，特别是当遇到曲率较大曲面时，将其规划成自然二次曲面，可有效地减少分片数，提高喷涂轨迹规划效率及涂层均匀性。

2.1 曲面离散点归类

首先，将曲面离散化，离散的方法是以一定密度的U向和V向等参数线将曲面分割，等参数线的交点即是离散点。根据离散点的几何参数可将离散点进行归类，其中当高斯曲率K＝0时，此类曲面为抛物面，可对此类曲面进行圆柱面或圆锥面拟合；当K＞0时，此类曲面为椭圆面，可对此类曲面进行球面拟合。

2.2 基于喷涂的最小二乘法曲面拟合

自然二次曲面包括圆柱面、圆锥面及球面。圆柱面方程：

式中，（x0，y0，z0）为圆柱面轴线上一点；（m，n，l）为圆柱面轴线方向的单位向量；ρ为圆柱面半径。

圆锥面方程：

式中，（x0，y0，z0）为圆锥面顶点；（m，n，l）为圆锥面轴线方向的单位向量；θ为圆锥面的半锥顶角。

球面方程：

式中，（x0，y0，z0）为球心；ρ为球面半径。

最小二乘法通常是通过求得目标函数的最小残差平方和，即

式中，（xi，yi，zi）为曲面上的离散点；n′为离散点总数。

为了在自然二次曲面拟合过程中体现喷涂精度的要求，有必要对影响喷涂精度的曲面几何特征进行分析。假设自然二次曲面上的喷枪轨迹优化后，最大涂层厚度为Tmax，平均涂层厚度为Td，最小涂层厚度为Tmin，原始曲面上任意一点S（xi，yi，zi）的涂层厚度为TS，拟合的自然二次曲面与原始曲面在该点处的法向偏角为αi，允许的极限法向偏角为αth。原始曲面上任意一点的涂层厚度满足：

若原始曲面上任意一点的涂层厚度满足：

若式（7）成立，可通过式（8）求解出极限偏角αth的值，即

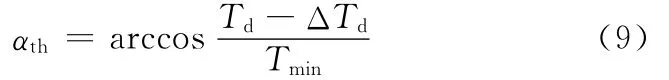
通过上述分析，只要自然二次曲面与原始曲面在任意点S处的法向偏角αi满足关系αi≤αth，原始曲面上的涂层厚度可由自然二次曲面上的涂层厚度近似表示。因此，在自然二次曲面拟合过程中，考虑到喷涂精度的要求，可将目标函数式（6）改写为

通过最小二乘曲面拟合后，曲面可分片规划成自然二次曲面的组合，可有效地减少传统喷涂分片方法下的分片数，提高喷涂轨迹规划效率。具体分片算法如下：

图4 算法流程图

3 自然二次曲面上喷枪轨迹优化

由于自然二次曲面上母线两侧的几何信息一致，为了便于分析自然二次曲面上涂层厚度的叠加和喷枪轨迹优化目标函数的建立，在这里指定曲面上的母线为喷枪轨迹。

喷枪的一条空间轨迹可定义为喷枪经过的一系列点的集合，设计时考虑一种可行的喷枪轨迹确定方法，即先指定期望的喷枪空间轨迹和喷涂方向，问题就转化为如何找到喷枪沿指定轨迹的最优时间序列，使得喷枪沿此轨迹进行喷涂作业时所定义的优化目标达到最优。因此，轨迹优化问题就把每一时刻的最优变量个数从一般喷枪轨迹优化问题中的6个（喷枪的位姿）减少为1个，简化了问题的复杂性。为了保证喷涂区域内涂层厚度的均匀，重要的是优化喷枪走速v和轨迹间距δ或喷涂半径R。

图5所示为喷枪在半径为ρ的凸圆柱面上的喷涂过程，喷涂区域在平面上的投影为椭圆形区域，其长短轴长度分别为a和b，S＊为点S在第一条轨迹上的投影，x表示喷涂范围内某点S到第一条轨迹的距离，O点为喷枪中心的投影点，则S点的涂层厚度为

图5 圆柱面上计算示意图

为了使喷涂区域内的涂层厚度尽可能均匀，这里取S点的实际涂层厚度与理想涂层厚度间的方差最小为优化目标函数：

为了使喷枪轴线始终垂直于圆弧面，喷枪需以圆弧面轴心旋转一定的角度β，而优化值δ正好是角度β确定的弦长，则两相邻轨迹间喷枪的转角为

用母线规划圆锥面上的喷枪轨迹时，喷枪喷射方向始终垂直于表面，令其轨迹间距在许用范围内[δmin，δmax]呈单调变化，则此时喷枪轨迹的优化实际上就是轨迹上喷枪速率及喷涂半径的优化。为了降低问题的复杂性，这里将喷枪轨迹分割为n段，若将相邻轨迹上的分割点以直线连接，则形成n个等腰梯形，其等腰梯形的上下底分别为δ1，δ2，…，δn＋1，并设定每段路径上的喷枪速率恒定，且该段路径上的轨迹间距为该段路径所在等腰梯形的中位线长度，这里具体分析第i段路径上涂层厚度的叠加情况，此时轨迹与等腰梯形中位线间夹角为θ，喷枪速率为vi，轨迹间距为δi，喷涂半径为Ri，相邻轨迹间喷枪转角为β，图6示出了喷枪在凸圆锥面上的喷涂过程。

图6 圆锥面上喷枪轨迹分段及计算示意图

在图6a中，轨迹与中位线夹角为

相邻轨迹间喷枪转角为

式中，H为圆锥面形成的圆锥体的高；D为圆锥体底面圆半径。

根据图6b，点S的涂层厚度为

式中，T1（x）和T2（x）分别为喷涂时两相邻轨迹上S点的涂层厚度；t1和t2分别为两条相邻喷涂轨迹上喷枪在S点喷涂时间的一半；t为喷枪从点O运动到点S＊的时间；ρi为点S在圆锥面法向上到圆锥面轴线的距离。

根据式（11），则优化目标函数可表示为

式中，ΔTd为允许的涂层厚度偏差。

球面上的母线实质就是经线，在用经线规划球面上的喷枪轨迹时，喷枪始终沿着经线轨迹垂直于球面，指向球心，令轨迹间距[δmin，δmax]在赤道线的一侧是单调变化的，与圆锥面喷涂轨迹优化方法类似，这里喷枪轨迹的优化实际上就是轨迹上喷枪速率及喷炬半径的优化，且经线轨迹相对于赤道线是对称分布的。为了降低问题的复杂性，这里将喷枪经线轨迹分割为n段，使轨迹间相邻分割点围成的曲面可近似看作平面，如图7a所示的等腰梯形面，喷枪的喷射方向与轨迹两侧对称梯形面的平均法向一致，且沿着等腰梯形的腰行走，n个等腰梯形的上下底分别为δ1，δ2，…，δn＋1，每段等腰梯形腰与下底边形成的夹角分别为θ1，θ2，…，θn。对于分割成的n段等腰梯形，再分别第二次分割成m段更短的路径，并设每段路径上的喷枪速率恒定，这里具体分析第i个等腰梯形上第k段路径上的涂层厚度叠加情况，此时轨迹与等腰梯形底的夹角为θi，喷枪速率为vik（i＝1，2，…，n；k ＝1，2，…，m），轨迹间距为δik，喷炬半径为Rik，相邻轨迹间喷枪转角为βik，喷枪在凸球面上的喷涂过程如图7b所示。

在图7a中，第i个梯形的上底为

下底则为第i－1个梯形的上底，特别地，若γ0＝0°时，δ0＝δmax，则第i个等腰梯形中第k段路径的轨迹间距为

第i个等腰梯形中轨迹与底的夹角为

第i个等腰梯形中第k段相邻轨迹间喷枪转角为

图7 球面上喷枪轨迹分段及计算示意图

式中，βi为第i个梯形的上底端点与球心连线形成的夹角；γi为第i个梯形的上底与球心所形成的三角面与赤道面的夹角。

根据图7b所示，点S的涂层厚度为

根据式（15），则优化目标函数可表示为

对于这里的多变量优化问题，可采用MATLAB7.0优化工具箱中的模式搜索法求解出各优化目标函数参数的优化值。

4 自然二次曲面交界处喷枪轨迹优化

在工业生产中，喷涂对象往往是大型工件，对工件曲面进行喷涂分片规划后，曲率较小区域被拓扑形成若干个近似平面片，曲率较大区域拟合成自然二次曲面，且自然二次曲面多与平面交接，如图8所示的汽车后保险杠，其曲率较小的前端被分片规划成近似平面片，曲率较大的两侧被分片规划成自然二次曲面。因此，本文在这里重点讨论平面与自然二次曲面交界处的喷枪轨迹优化。根据文献[11]所得到的结论，设计喷枪轨迹时，尽量保证面片交界处的喷枪轨迹与交界线平行，可有效提高面片交界处的涂层均匀性。下面以圆柱面和圆锥面与平面的交界为例，图9所示为圆柱面和圆锥面与平面交界的情况，对交界处的喷枪轨迹优化进行分析，此时保持两面片上优化得到的喷枪速率不变，需要优化的是平面上喷枪轨迹到交界线的距离h1和喷枪由平面过渡到圆柱面和圆锥面上的转角β。

图8 汽车后保险杠

根据图9a所示，圆柱面与平面交界处某一点S的涂层厚度可表示为

喷枪由片1到片2的转角为

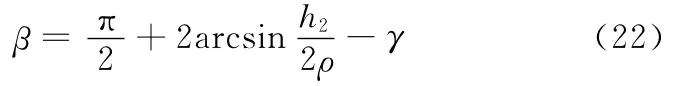
根据图9b所示，圆锥面与平面交界处某一点S的涂层厚度可表示为

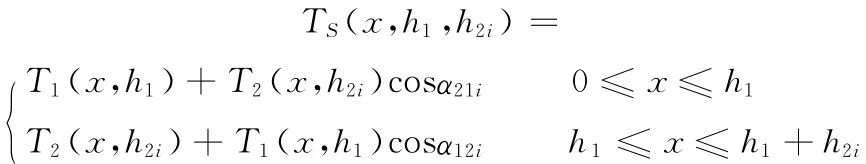
图9 圆柱面和圆锥面与平面交界计算示意图

则建立优化目标函数为

喷枪由片1到片2的转角为

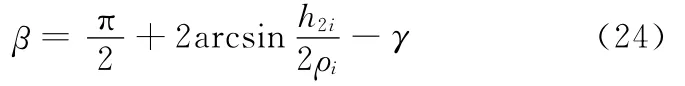
同样，运用模式搜索法可对式（21）、式（23）中的多变量问题进行求解。

5 仿真试验

设理想涂层厚度为Td＝50μm，允许的涂层厚优化平板上的喷枪轨迹间距范围为[50.0，60.9]mm。对于目标函数的优化计算，均采用MATLAB 7.0软件优化工具箱中的模式搜索工具箱进行计算。

设圆柱面半径ρ＝300mm，根据式（11）、式（12）优化后得到喷枪速率和相邻轨迹间的喷枪转角分别为322.7mm／s和11.6°，此时最大和最小涂层厚度分别为50.9μm和48.3μm。

设圆锥面底面圆半径D＝200mm，高H＝300mm，根据式（13）得到夹角θ＝85.15°，令n＝8，每段区间形成的等腰梯形的上底和下底分别为δ1＝50.00mm，δ2＝51.36mm，δ3＝52.73mm，δ4＝54.09mm，δ5＝55.45mm，δ6＝56.81mm，δ7＝58.18mm，δ8＝59.54mm，δ9＝60.90mm。根据式（15）优化后得到喷枪速率和喷涂半径如表1所示，此时最大和最小涂层厚度分别为50.8μm和48.6μm，由式（14）得到相邻轨迹间喷枪转角β＝14.6°。图10所示为喷涂过程中圆锥面上喷枪轨迹间距与喷枪速率及喷涂半径的曲线关系。度误差ΔTd＝10μm，圆锥张角φ＝45°，喷枪的喷射高度h许用范围为[99.2，120.7]mm，喷枪喷出的圆锥形涂料流底面半径R的许用范围为[41.1，50.0]mm，通过平板上的喷涂试验数据得到涂层累积速率为

表1 喷枪速率及喷涂半径的优化结果

图10 圆锥面上轨迹间距与喷枪速率、喷涂半径的曲线关系

设球面半径ρ＝203.5mm，令n＝m＝4，根据式（16）、式（17）得4个等腰梯形的上下底分别为δ1＝60.9mm，δ2＝60.1mm，δ3＝58.0mm，δ4＝54.6mm，δ5＝50.0mm；由式（18）得到轨迹与轨迹间距的夹角分别为θ1＝89.33°，θ2＝88.67°，θ3＝88.02°，θ4＝87.39°。根据式（20）优化后的喷枪速率及喷涂半径如表2所示。涂层厚度的最大值与最小值分别为50.8μm和48.7μm。图11所示为轨迹间距与喷枪速率、喷枪转角及喷涂半径间的曲线关系。

表2 喷枪速率及喷涂半径的优化结果

图11 球面上轨迹间距与喷枪速率、喷涂半径及喷枪转角的曲线关系

设圆柱面和圆锥面与平面在交界处相切，此时γ＝90°，圆柱面半径ρ＝300mm，圆锥面底面圆半径D＝200mm，高H＝300mm。喷枪在平面上的喷涂半径R＝50mm，喷枪在圆锥面上喷涂半径的许用范围为[41.1，50.0]mm。平面上喷枪轨迹优化后得到喷枪速率v＝325.6mm／s。优化圆柱面上的喷枪速率为322.7mm／s，保持平面和圆柱面上喷枪速率不变，根据式（21）、式（22）优化得到h1＝30.2mm，β＝5.7°，此时交界处的最大和最小涂层厚度分别为51.1μm和48.2μm。优化圆锥面上的喷枪速率如表1所示，保持平面和圆锥面上喷枪速率不变，根据式（23）、式（24）优化得到h1＝29.9mm，β＝7.1°，由于平面和圆锥面交界处是不同喷涂半径下的涂层叠加，因此，随着圆锥面上喷涂半径的变化，涂层厚度最大值和最小值如图12所示。

图12 圆锥面与平面交界处涂层厚度极值

6 结论

（1）结合喷枪3D模型的运用，在减少曲面分片数量的前提下，基本能将涂层厚度误差控制在±2μm。

（2）通过对圆锥面及球面上有限点喷枪参数的拟合，发现喷枪速率随轨迹间距呈非线性变化，其他参数基本呈线性变化。

（3）通过对圆柱面和圆锥面与平面交界处喷枪轨迹优化目标函数的建立，能有效地提高面片交界处的涂层均匀性。

[1]王振滨，赵德安，王燚，等.喷漆机器人离线编程系统探讨[J].江苏理工大学学报：自然科学版，2000，21（5）：78-82.

[2]王燚，赵德安，王振滨，等.喷漆机器人喷枪最优轨迹规划的研究[J].江苏理工大学学报（自然科学版），2001，22（5）：55－59.

[3]Antonio J K，Ramabhadran R，Ling T L.A Framework for Trajectory Planning for Automated Spray Coating[J].International Journal of Robotics and Automation，1997，12（4）：124－134.

[4]Chost H.Coverage of Known Spaces：the Boustrophedon Cellular Decomposition[J].Autonomous Robots，2000，9（12）：247－253.

[5]Atkar P N，Chost H，Rizzi A.Toward Optimal Coverage of 2－dimensional Surfaces Embedded in Choice of Start Curve[C]∥Proceedings of the 2003 IEEE／RSJ International Conference on Intelligent Robots and Systems.Las Vegas，2003：3581－3587.

[6]Wei Huasheng，Chen Heping，Xi Ning.Tool Path Planning for Compound Surfaces in Spray Forming Processes[J].Automation Science and Engineering，2005，2（6）：240－249.

[7]刘能广，任天然，柴苍修，等.基于遗传算法的喷漆机器人轨迹的二层规划[J].机械设计与制造，2008（6）：173－175.

[8]李发忠，赵德安，姬伟，等.面向凹凸结构曲面的喷漆机器人轨迹优化研究[J].江苏科技大学学报（自然科学版），2008，22（4）：64－67.

[9]Conner C D，Greenfield A，Atkar N P，et al.Paint Deposition Modeling for Trajectory Planning on Automotive Surfaces[J].IEEE Transactions on Antomation Science and Engineering，2005，2（4）：381－392.

[10]Chen Heping，Xi Ning.Automated Tool Trajectory Planning of Industrial Robots for Painting Composite Surfaces[J].Adv.Manuf.Technol.，2008，35：680－696.

[11]Chen Heping，Thomas F，Li Xiongzi.Automated Industrial Robot Path Planning for Spray Painting Process：A Review[C]／／4th IEEE Conference on Automation Science and Engineering.Washington D C，2008：522－527.

[12]曾勇，龚俊，陆保印.面向直纹曲面的喷涂机器人喷枪轨迹优化[J].中国机械工程，2010，21（17）：2083－2089.

[13]Persoons W，Brussl H V.Cad－based Robotic Coating with Highly Curved Surfaces[C]∥Proceedings of ISIR’93.Tokyo，1993：611－618.

[14]Goodman E D，Hoppensteradt L T W.A Method for Accurate Simulation of Robotic Spray Application Using Empirical Parameterization[C]∥Proceedings of the 1991IEEE International Conference on Robotics and Automation.Sacramento，1991：1357－1368.

[15]Anita H，Per N.Models for the Simulation of Spray Deposition and Robot Motion Optimization in Thermal Spraying of Rotating Objects[J].Surface and Coatings Technology，1999，12：191－201.

[16]陈伟，赵德安，汤养.自由曲面喷漆机器人喷枪轨迹优化[J].农业机械报，2008，39（1）：147－150.