抛光机磨头磨块座振动问题求解及实验

徐 斌 邵俊鹏 刘 嘉

哈尔滨理工大学，哈尔滨，150080

0 引言

陶瓷抛光砖是现代建筑装修工程中应用最为广泛的陶瓷制品之一。审美要求的日益提高，对陶瓷砖的表面加工质量提出了更高的要求。文献[1-8]通过试验得出了抛光瓷砖在抛光过程中表面粗糙度的变化规律，认为抛光瓷砖气孔的减少对机械加工的难度有很大的影响。李松等[9]通过试验得出瓷砖的抛光轨迹以及磨头转速对瓷砖抛光质量的影响规律。目前应用最为广泛的是摆动式瓷砖抛光机，但是该抛光机在抛光过程中出现了表面粗糙度不均匀、瓷砖震碎、瓷砖崩角等问题。针对这些问题，汤迎红等[10]优化了抛光盘的凸轮曲线，解决了柔性冲击问题。吴南星等[11]用加水法来控制噪声。瓷砖在生产加工过程中，磨头振动引起的碎砖问题一直存在，给企业的生产带来损失，影响了抛光机的可靠性。近年来对瓷砖抛光机振动机理和减振措施的研究成为瓷砖生产企业和设备生产厂家要解决的重点问题。

笔者在前人研究的基础上，以摆动式抛光机磨头磨块座为研究对象，利用差分法求解磨块座的振动频率，并进行实例计算和实验。通过实验来分析磨块座的振动频率对碎砖的影响，以及主轴频率的合理控制范围。

1 摆动式磨头的工作原理

图1为摆动式抛光磨头工作原理图，磨头工作原理为：电机4驱动主动带轮5，通过传送带又驱动从动带轮3（从动带轮3与磨头主轴、磨头壳体以及主动齿轮6刚性连接在一起）。从动带轮3带动磨头壳体实现公转，同时从动带轮带动主动齿轮6转动。主动齿轮6驱动从动齿轮1、凸轮2旋转（从动齿轮与凸轮2刚性连接在一起）。磨头壳体在公转的同时，通过差动（主动齿轮6与从动齿轮1相差两齿）轮系，使凸轮2相对磨头壳体产生一个相对转动，凸轮2驱动主动摆杆13，主动摆杆又驱动从动摆杆7，使连接在摆杆上的磨块座8、12做往复摆动。

图1 摆动抛光磨头原理示意图

2 磨块座的数学模型

磨头由6个磨块座（大小和形状完全一样，均匀分布在磨头底部）支撑，故拿出一个磨块座做具体的力学分析。根据磨头的结构和运行情况，将磨块座简化为悬臂梁来建立力学模型。

2.1 磨块座的横向自由振动方程

将磨块座简化为一个悬臂梁，如图2所示，图中的w为格点处的横向位移。等截面悬臂梁的横向强迫振动方程[12]为

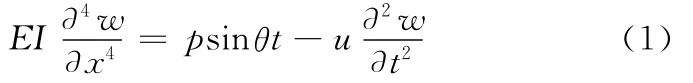
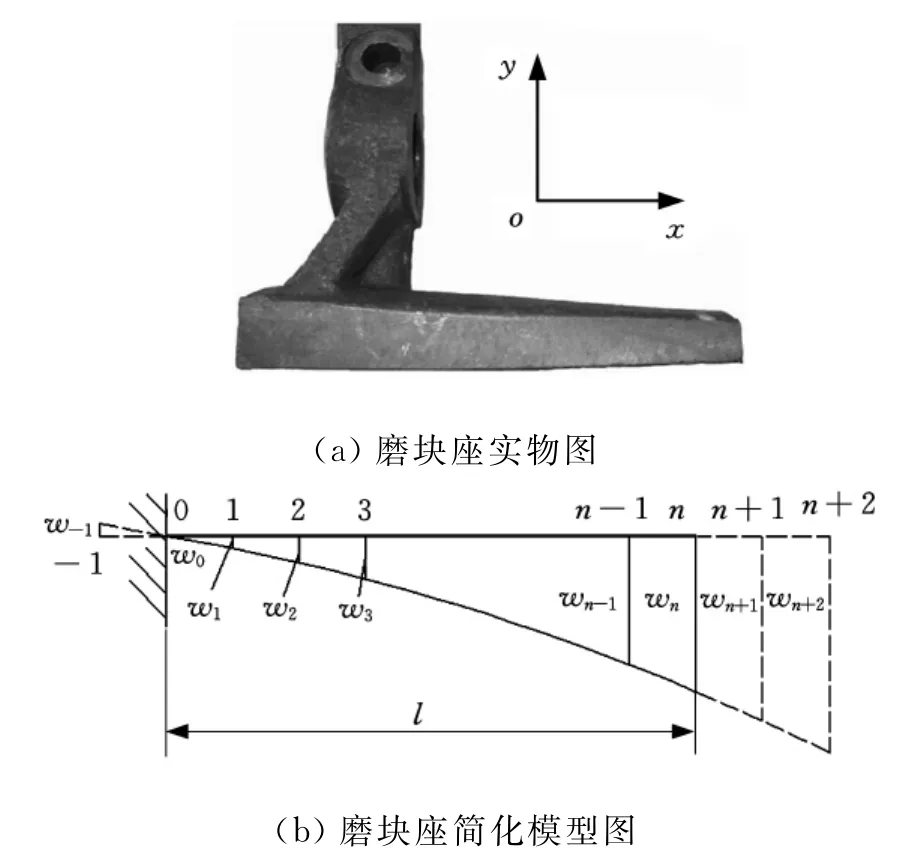
图2 磨块座实物及简化模型图

式中，u为单位梁长的自重；psinθt为作用在梁上的强迫振动载荷；E为磨块座的弹性模量；I为磨块座的截面惯性矩；θ为振动载荷频率；p为振动载荷的幅值；t为时间。

悬臂梁上无载荷作用时，psinθt＝0。因此磨块座的自由振动方程为

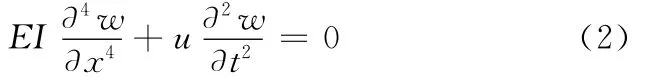
磨块座的横向位移U（x，t）为

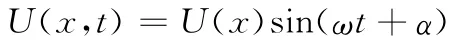
式中，U（x）为磨块座振动时的振幅；ω为磨块横向振动频率；α为相位角。

2.2 磨块座的横向振动有限差分方程

有限差分法是一种直接从相应问题的微分方程出发的离散化方法。根据微分的原理以近似的有限差分式来代替微分方程及边界条件，将微分方程变换成一组有限个线性代数方程，容易求解磨块座简化悬臂梁模型的固有振动频率。

根据文献[13-14]利用式（4），将式（3）转化为任意节点的有限差分方程：

式中，λ为节点的格距，λ＝l／n；n为格点数。

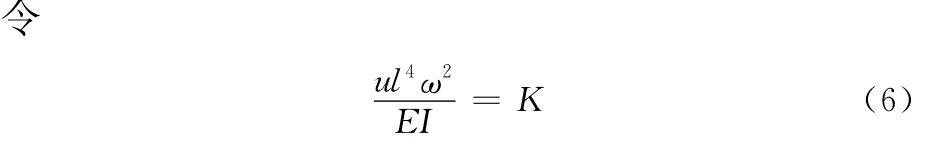
代入式（5）整理得磨块座横向振动有限差分方程：

将式（7）的格点和系数绘制成网格，如图3所示。

2.3 磨块座模型的格点划分

为了便于计算，分析时将磨块座简化的悬臂梁模型等分成n段，每段的长λ＝l／n。以各段的分界点为节点，它们连同两端的节点的编号为0，1，…，n。依格点划分布局，如图3所示。从磨块座有限差分方程的网格图可以看出，每个节点的差分方程包含零点及与零点相邻的点。因为悬臂梁为自由边界，因此磨块座模型的节点划分就包含着虚格点n＋1、n＋2，还有－1格点。

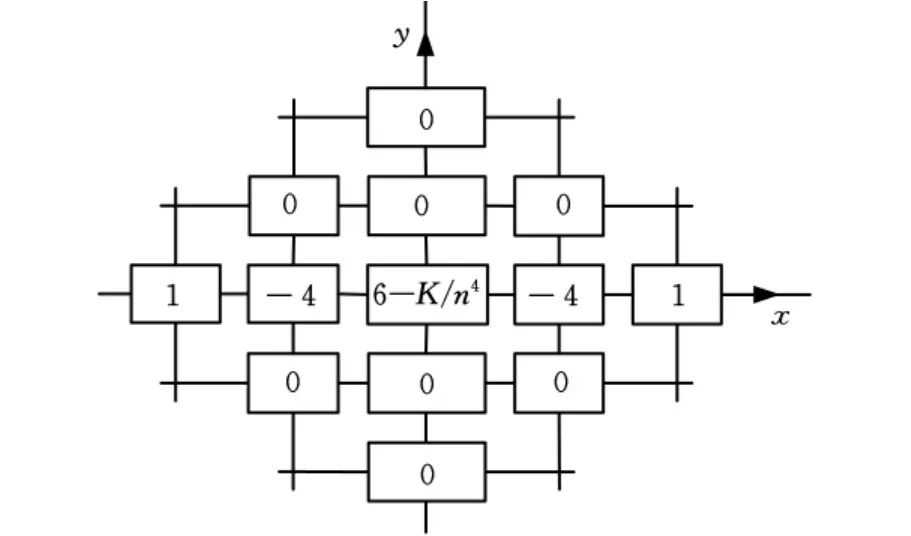
图3 磨块座结点有限差分方程网格图

2.4 磨块座的边界条件及其差分方程

磨块座简化为悬臂梁，一端固定，另一端自由。固定端处（x＝0）的边界条件为

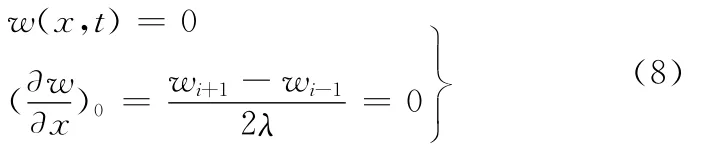
根据式（8）得出

根据式（9）得出，w1＝w－1。固定端边界处的w＝0。

自由端（x＝b）的边界条件为

由式（10）可以得出

磨块座简化为悬臂梁模型，x＝b端为自由端。端点的w也需要取为未知值，并为此节点列出差分方程（式（7））。这些方程中将包含边界外两行虚节点处的w。但是，可以利用自由边界条件，列出虚节点的关系式，把虚节点处的w用边界上以及边界内节点处的w表示。自由端外的第1个和第2个虚节点要用边界条件（式（11））来计算。

2.5 磨块座横向振动频率方程

根据任意节点处的差分公式（式（7））以及边界条件（式（9）～ 式（11）），可求解出K。差分的误差值和格点的疏密有关系，n的数值越大，得出的结果就精确。但是在求取的K值中必然存在着误差，为了得出精确的数值，用李却德孙外推法[14]进行数值修正：

式中，Ka，b为修正后的系数；Ka、Kb为系数；下标a、b为分段数，a，b＝1，2，…，n，且a＜b。

根据式（12）和式（6）得出磨块座横向振动频率：

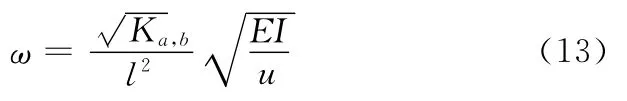
3 计算实例

抛光机在加工瓷砖时，磨头气缸对磨头施加恒定压力，气缸工作压力为0.05～2MPa；磨头底面由6个磨块座支撑，磨块座摆动中心到底面的距离l＝90mm；座长165mm，宽65mm，高12mm；磨块材料——铸铁的弹性模量E＝160GPa，惯性矩I＝9.36×10－8m4，重1.3kg。

当n＝2，3，4，5，6时分别求解K 值，并用李却德孙外推法（式（11））依次修正K后得出表1。

经李却德孙外推法修正后，得出比较精确的结果K＝12.59。将其代入磨块座横行振动频率公式（式（13））得出磨块座的横向自由振动频率ω＝5.68Hz。

4 实验

4.1 实验装置和参数

实验所用的抛光机为SD－281型12磨头的瓷砖抛光机，应用其中的1个磨头进行实验。瓷砖规格是800mm×800mm，共16块。测振仪型号为TV100。实验装置如图4a所示。每个实验用时11min。振动测试设备如图4b所示。抛光机磨头根据实验的要求在加工过程中由导轨10带动滚轮往复运动。实验时应用测振仪11测试磨头上3个方向的测点，分别是X方向测点4、Y方向测点3、Z方向测点9。

图4 实验装置和振动测试设备

4.2 实验结果与分析

按照表2所示的参数进行了16组实验。实验结果如图5所示。

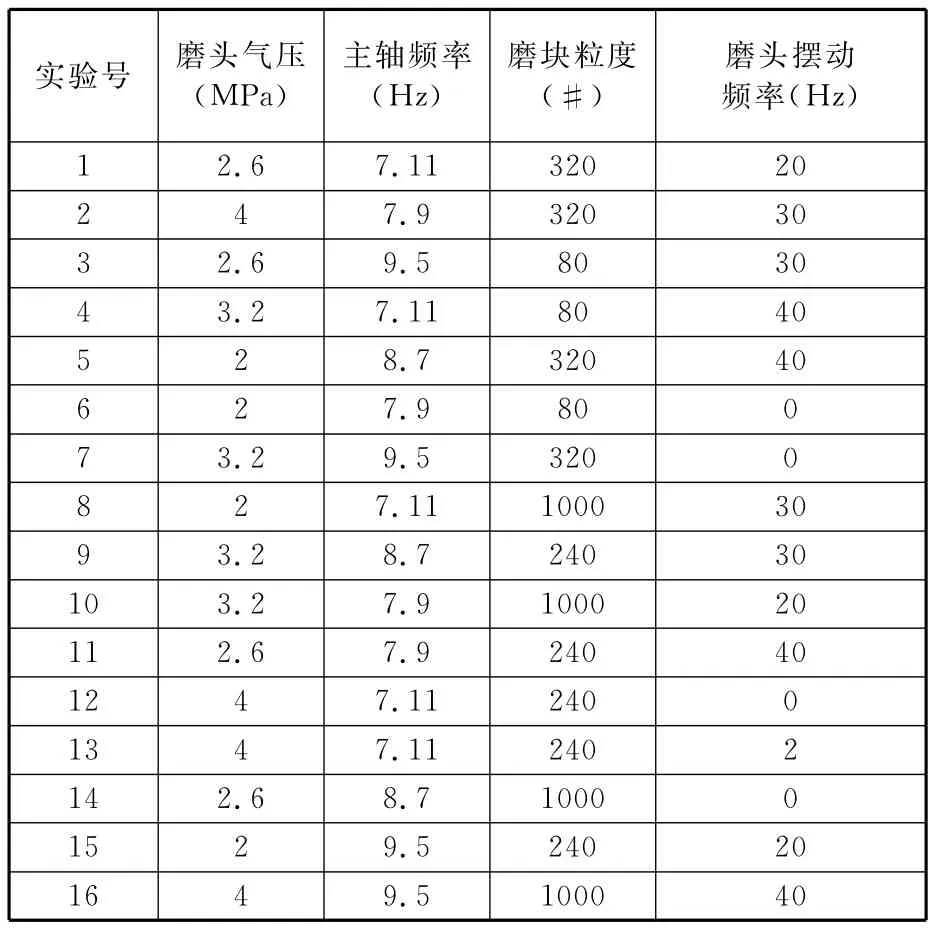
表2 磨头振动加速度实验参数

通过分析图5中3个方向的振动加速度得出，Z方向的磨头振动加速度要远大于X、Y方向的磨头振动加速度，磨头垂直方向的振动为主要振动。同时还看出，在Z方向的磨头振动加速度呈正弦波周期性变化。造成这一变化规律的原因是磨头凸轮2的正弦波形面驱动主动摆杆13绕着主动摆杆轴摆动（图1），凸轮2每转过一个波峰，主动摆杆就摆动一个来回。摆动时，波峰的2个面交替驱动主动摆杆13，在交替驱动过程中，凸轮2的正弦波工作面会对主动摆杆产生冲击振动。

从图5可得出：在相同的主轴频率下，磨块粒度越小，Z方向磨头振动加速度就越大。在相同磨块粒度下，主轴的频率越大，Z方向磨头振动加速度也就越大。但磨块粒度大于1000＃ 时，主轴的频率、压力、摆动速度的变化对Z方向磨头振动加速度的影响很小。当磨头的摆动频率为0时，Z方向磨头振动加速度为最大。因此磨头在摆动到瓷砖的两端时停留的时间不可以超过20s。

按照实验编号为12的参数进行实验时，磨头振动很大，磨头运行60s后，磨头产生共振，瓷砖碎裂。磨头振动加速度如图5l所示。从图5l可以看出，Z方向的磨头振动加速度为16个实验中最大的。磨头共振后的实物和碎砖如图6所示。这一实验中，主轴的频率为7.11Hz，与通过实例中得出的磨块座的横向自由振动频率5.68Hz相近，产生了共振。磨头的剧烈振动将瓷砖振碎。

通过图5的实验数据分析可知，若将主轴频率控制在8.7Hz时，磨头在Z方向的振动加速度就会很小。

还用实验编号为12的参数，把摆动频率改为2Hz，即按照实验编号为13的进行实验，实验后得出的结果如图5m所示。从图5m中可以看出，X、Y、Z三个方向的振动加速度很小，频率改变可以削弱磨头共振。

5 结论

（1）由理论分析得出磨块座的横向自由振动频率为5.68Hz。

（2）由实验得出磨头垂直方向振动加速度呈正弦波规律变化。

（3）加工过程中，磨块的粒度越小，磨头振动越大。

（4）磨头的摆动有利于减小磨头共振，磨头在摆动到瓷砖两端时，停留时间不可以超过20s。

（5）主轴频率与磨块座频率共振是碎砖的主要因素。

图5 实验测得的3个方向振动加速度

[1]Orts M J，Sanchez E，Gareia－Ten，et al.PorcelainTile Behavior during Polishing[J].Bol.delaSoe.EsP.de Ceramicay Vidrio，2001，40：447-455.

[2]Hutchings I M，Xu Y，Sanchez E，et al.Porcelain Tile Microstructure：Implications for Polishability[J].Journal of the European Ceramic Society，2006，26（6）：1035－1042.

[3]Sanchez E，Ibanez M J，Garcia－Ten J，et al.Porcelain Tile Microstructure：Implications for Polished Tile Properties[J].Journal of the European Ceramic Society，2006，26（13）：2533－2540.

[4]Sousa F J P，Aurich J C，Weingeartner L，et al.Kinematics of a Single Abrasive Particle during the Industrial Polishing Process of Porcelain Stoneware Tiles[J].Journal of the European Ceramic Society，2007，27（10）：3183－3190.

[5]Xu X P，Huang H，Gao Y，et al.Processes for the Generation of Glossiness on Ground Granites and Ceramics[J].Key Engineering Materials，2003，238（2）：99－104.

[6]Wang C Y，Kang T C，Qin Z，et al.How Abrasive Machining Affects Surface Characteristics of Vitreous Ceramic Tile [J].American Ceramic Society Bulletin，2003，82（10）：9201－9208.

[7]Tucci A，Esposito L，Malmusi L，et al.Wear Resistance and Stain Resistance of Porcelain Stoneware Tiles[J].Key Engineering Materials，2002，206（2）：1759－1762.

[8]Braganca S R，Bergmann C P.A View of Whitewares Mechanical Strength and Microstructure[J].Ceramics Intenational，2003，29：801－806.

[9]李松，郑超.抛光砖面磨抛均匀性浅析 [J].陶瓷，2005（7）：19-21.

[10]汤迎红，吴运新，周鹏.陶瓷抛光机抛光盘凸轮的改进设计[J].机械设计，2006（3）：58－60.

[11]吴南星，朱金贵，肖任贤.陶瓷用抛光机磨头声－结构分析及噪声控制[J].陶瓷学报，2009，30（1）：101－105.

[12]程耀东.机械振动学（非线性系统.弹性体）[M].杭州：浙江大学出版社，1990.

[13]曹志远.板壳振动理论[M].北京：中国铁道出版社，1989.

[14]曹国雄.弹性矩形薄板振动[M].北京：中国建筑工业出版社，1983.