磁悬浮球形磁阻电动机产生悬浮力和磁力矩的机理分析

曾 励 王 军 张 丹

扬州大学，扬州，225127

0 引言

球形电动机为多自由度电动机，有2个或3个旋转自由度，可以绕过定点的空间轴线旋转，在机器人的关节及机械手的关节等具有多个运动自由度的设备中具有广阔的应用前景[1－2]。从20世纪50年代开始，机器人、空间技术及自动化技术的迅速发展，促进了多自由度球形电动机原理和结构研究的发展[3－6]。球形电动机机械集成度高，在有多个运动自由度的机械系统中，一个多自由度的球形电动机可以代替两台或多台单自由度电动机实现机械系统多自由度的驱动，大大简化机械系统的结构和运动传动链，减小体积和质量，可以消除由于齿轮传动带来的齿隙和摩擦，从而提高系统的效率、精度和动态性能，性能价格比高，在控制和轨迹规划方面占有优势。但是，目前的球形电动机为了实现不同自由度的旋转，一般采用框架结构，每一层框架由机械轴承支承绕一个坐标轴旋摆，因此存在结构复杂、体积较大、旋转角度受到限制等缺点。在高速、超高速的多自由度装置中，机械摩擦不仅增加了关节的摩擦阻力，而且造成部件发热，严重时会导致系统的动态特性变差。因此，笔者针对现有球形电动机存在的上述问题，基于磁悬浮技术和电动机技术，设计一种机械集成度高、结构简单、无摩擦、无磨损，精度高和动态性能好，并能使球形转子俯仰、摇摆和偏转的角度达到最大，具有可以绕球形转子中心旋转的二自由度或多自由度磁悬浮球形磁阻电动机，并对其工作机理和悬浮控制进行研究。

1 磁悬浮球形磁阻电动机的基本结构

磁悬浮球形电动机的定转子三维结构如图1所示，转子为一开有沟槽的单元凸极球体（位于电动机的中间）。在球形转子的赤道线位置对称分布有4个定子，其中，定子1与定子3对称于球形转子，沿X轴方向保持同轴，其作用是驱动转子绕X轴旋转，并产生使转子在X轴方向产生稳定悬浮的磁悬浮力；定子2与定子4对称于球形转子，沿Y轴方向保持同轴，其作用是驱动转子绕Y轴旋转，并产生使转子在Y轴方向产生稳定悬浮的磁悬浮力。定子5布置在球形转子的顶端并与Z轴同轴，其作用是驱动球形转子绕Z轴旋转并产生Z轴方向的稳定悬浮力。

图1 磁悬浮球形电动机结构图

磁悬浮球形电动机球形转子的球面上开有相互正交的槽，定子为包含6个凸极和1个阶梯的圆环结构，定子凸极上按磁阻电动机原理绕有驱动转子旋转的多相绕组。各相绕组通电后除产生驱动转子旋转的电磁转矩以外，还为转子提供径向磁悬浮力。

2 磁悬浮球形磁阻电动机的气隙磁能

磁悬浮球形电动机的分析研究方法与其他磁悬浮无轴承电动机的分析研究方法一样，可从电动机定子和转子之间的气隙磁能着手，即根据气隙磁能建立电动机的机－电能量转换关系，进而得出驱动转子的电磁转矩和使转子悬浮的电磁悬浮力的关系。为了简化分析，先作以下假设：①三相定子绕组在空间对称分布，各相电流所产生的磁势在气隙空间正弦（或余弦）分布，忽略其高次谐波分量；②忽略槽漏感、端部漏感及磁饱和效应；③由于转子与平衡位置的偏移非常小，故认为定子和转子凸磁极面平行；④忽略铁芯磁阻和涡流损耗，整个磁路系统只考虑工作气隙的磁阻。

磁悬浮球形电动机转子的球心未发生偏移时，定子凸极包络球面半径为R，转子凸极包络球面半径为Rr，定子凸极内径与转子凸极外径之间的间隙g0＝R－Rr。取定子的对称轴与Z轴重合，建立坐标系f（X，Y，Z）＝F（R，φ，θ），如图2所示。在定子6个磁极表面包络成的球面环上，取宽为Rdφ、长为rdθ的微小球面，其面积ΔA＝（rdθ）·（Rdφ），φ1＜φ＜φ2，0＜θ＜2π。若电动机转子在干扰作用下，转子球心由O点移到了O1点，沿Z轴方向的偏移量为z，在Rr≫z时，定子磁极包络环形球面上任意位置定转子凸极包络面之间的径向间隙长度为

图2 转子气隙变化示意图

磁阻电动机球形转子在转动过程中，其某一凸极表面与定子磁极凸极表面部分重叠对齐，产生磁拉力，形成电磁转矩，该磁拉力亦为使转子悬浮的磁悬浮力。因此定子磁场产生的磁通流向球形转子时，经过的气隙长度变化复杂，一般为φ和θ的函数，即δc＝gc（φ，θ），故其磁导也是φ和θ的函数Λ（φ，θ）。根据文献[7]对轴向平面悬浮驱动的磁悬浮磁阻电动机磁导的处理方法，可假设提出的轴向球面悬浮驱动的磁悬浮磁阻电动机的单位面积微磁导与定转子之间凸极磁极对齐间隙e成反比，并按余弦规律分布，即

式中，K0、K为磁导常数，与定转子凸极结构等有关；ω为转子相对于定子转动的角速度；ψ为某定子驱动转子绕定子坐标轴旋转时与定子之间的相位差；e为定子凸磁极和转子凸磁极之间的径向间隙。

由于定子磁极包络球面环的宽度较小，即φ（φ1＜φ＜φ2）的变化范围很小，为便于计算，可认为定子磁极面与转子对齐的磁极面平行，即e可表示为

式中，φ0为定子磁极形心位置处法线与Z轴的夹角。

磁场在定转子间的气隙中产生的微磁能为

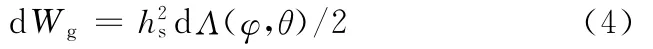
式中，hs为定子绕组在气隙上的磁势（磁压）。

磁势hs即安匝数，一般按正弦或余弦规律分布[7]，设为

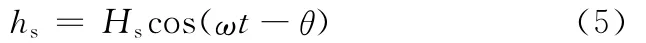
式中，Hs为磁势幅值，Hs＝NI。

对式（4）进行定积分，得气隙总磁能：

式（6）为磁悬浮球形磁阻电动机气隙磁能的数学描述，描述了磁悬浮球形磁阻电动机的机－电能量转换关系。利用电动机的气隙磁能分别对转子与定子之间的相位差以及转子的径向位移求导，可得到磁悬浮球形磁阻电动机的电磁转矩和电磁悬浮力。

3 磁悬浮球形磁阻电动机的磁悬浮力和磁转矩

3.1 磁悬浮球形磁阻电动机产生的磁悬浮力

由式（6）对z求导可得磁悬浮球形磁阻电动机沿Z轴方向的电磁悬浮力：

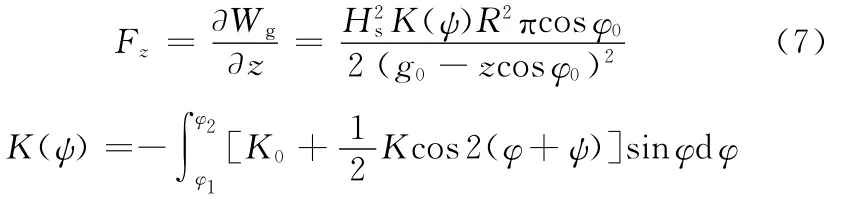
由式（7）可见，磁悬浮球形电动机在Z轴方向产生的磁悬浮力与转子凸磁极和定子凸磁极之间的间隙g0－zcosφ0的平方成反比，与绕组产生的磁势Hs的平方成正比，因此通过改变磁势（或绕组电流）大小就可以控制球形转子沿Z轴方向的偏移位移z，使电动机转子达到稳定悬浮。

同理可推出其他方向具有相同结构定子的电磁悬浮力表达式。磁悬浮球形磁阻电动机在某个坐标轴（如X轴）方向上，有对称于转子的2个定子驱动转子沿该坐标轴的悬浮与旋转。当稳定悬浮的转子在干扰作用下沿坐标轴偏离平衡位置时，为了使转子恢复到原来的平衡位置，则在控制器作用下，靠近间隙减小侧定子的绕组电流将减小，使该定子与转子间的气隙磁势随之减小，ΔHx变为Hx0－ΔHx；靠近间隙增加侧定子的绕组的电流将增大，使该定子与转子间的气隙磁势随之增大，ΔHx变为Hx0＋ΔHx。因此该方向产生的磁悬浮力为

式中，ΔHx为由于绕组电流变化产生的磁势增量；Hx0为转子处于平衡位置（与定子包络球面同心）时的磁势。磁悬浮球型磁阻电动机在X轴方向上产生的总电磁悬浮力为

3.2 磁悬浮球形磁阻电动机产生的电磁转矩

由式（6）对ψ求导可得磁悬浮球形磁阻电动机绕Z轴的电磁转矩：

当z＝0时，转子在平衡位置时产生的电磁转矩为

由式（10）可见，通过改变定子绕组磁势Hs的大小及转子相对于定子的相位差ψ即可控制磁悬浮球形电动机转子绕Z轴电磁转矩的大小和方向。同理可推出X方向具有相同结构定子的电磁转矩表达式：

g0≫x时ΔHx很小，对电磁转矩的影响很小，可以忽略不计。因此，磁悬浮球形磁阻电动机产生的总电磁转矩可近似为

由式（12）可见，磁悬浮球形磁阻电动机的悬浮调节与控制对电动机的电磁转矩几乎不产生影响，这给电动机的悬浮和旋转的综合控制带来了方便。

4 磁悬浮球形磁阻电动机的控制

4.1 控制原理

磁悬浮球形磁阻电动机在同坐标轴方向的2个定子绕组可按磁阻电动机控制策略分别控制，2个电动机子系统同步驱动球形转子转动。由位移传感器检测出的转子偏移信号经过滤波、放大及悬浮控制器等环节的处理后变成电流（或电压）信号，将其反馈到绕组控制输入端，与输入的转矩电流（或电压）进行叠加来改变定子绕组中电流的大小，达到悬浮控制的目的，其控制系统原理如图3所示[8－9]。

图3 磁悬浮球形磁阻电动机的控制原理

4.2 径向控制结果

按图3所示的控制系统，2个定子子系统的控制原理和控制硬件电路均与电动机控制系统相同。因此，电动机的控制性能主要取决于系统的悬浮控制性能。

4.2.1 电动机启动过程仿真结果及分析

如图4所示，磁悬浮永磁球形电动机启动后，电动机转子由初始位置迅速向平衡位置起浮，并迅速稳定在平衡位置，上升时间小于0.3s，超调量控制在1%以内，稳定悬浮后无稳态误差，具有良好的动静态性能。

图4 电动机启动过程径向悬浮仿真

图5所示为输入频率为50Hz的正弦交流信号时，电动机转子基本稳定后，截取0.3～1.4s球形转子球心偏离平衡位置的运动轨迹。从图5可以看出，当电动机转子基本稳定后，转子位移均小于50μm。因此，可近似认为电动机转子处于中心平衡位置，实现了稳定悬浮。

图5 稳定后径向位移曲线图

4.2.2 电动机转子受到扰动仿真结果及分析

图6 阶跃信号对径向偏移的干扰

图6所示为电动机实现稳定悬浮后，分别于0.5s、0.8s对电动机转子输入正反两方向脉冲干扰的仿真结果。由图6可知，磁悬浮球形电动机在受到径向扰动后，能在短时间内恢复到平衡位置，上升时间均小于0.2s，且超调量小，不存在振荡现象。这表明，电动机径向悬浮控制系统具有良好的抗干扰能力。

5 结束语

设计了一种多自由度磁悬浮球形磁阻电动机的基本结构，研究了电动机产生电磁悬浮力和电磁转矩的机理，建立了电动机的综合控制系统，并进行了悬浮控制仿真。仿真结果表明，电动机系统具有良好的动静态性能和抗干扰能力。

[1]邹继明，崔淑梅，程树康.多自由度（旋转）电动机的发展[J].高技术通讯，2000（10）：103-105.

[2]叶继涛，陈儿同，王芳，等.一种新型二维自动旋转台的研制与应用[J].节能技术，2003，21（1）：34－35.

[3]Davey K，Vachtsevanos G，Powers R.The Analysis of Fields and Torques in Spherical Induction Motors[J].IEEE Trans.on Magn.，1987，23（1）：273－282.

[4]Kaneko K，Yamada I，Itao K.A Spherical DC Servo Motor with Three Degrees of Freedom[J].ASME Trans.Dynamic Systems Measurement and Control，1988，111（3）：398－402.

[5]Chirikjian G S，Stein D.Kinematic Design and Commutation of a Spherical Stepper Motor Experiments in the Commutation and Motion Planning of a Spherical Stepper Motor[C]／／ASME 2000Design Engineering Technical Conference and Computer and Information in Engineering Conference.Baltimore，2000：DETC00／MECH－14／15.

[6]佐佐江启介，五百井清，大筑康生，等.3自由度小型アクチユエタの开发（第1报）[J].精密工學會志，1995，61（3）：386－390.

[7]上野哲，岡田養二.ァキシャル磁気浮上回転モ—タの開発と制御[J].日本機械學會論文集（C編），1997（8）：2707－2713.

[8]曾励，张丹，戴敏.向心推／拉力磁悬浮球形磁阻电动机：中国，ZL200920039032.7[P].2010－02－17.

[9]曾励，张丹，戴敏.开关磁阻式磁悬浮球形主动关节：中国，ZL200920040447.6[P].2010－01－13.