基于最优加权的大面积金刚石膜衬底温度数据融合研究
汪洪波 李宏远
合肥工业大学,合肥,230009
0 引言
金刚石具有高透光、高传声和极佳的化学惰性,在科研和工业领域得到广泛应用。金刚石薄膜的均匀性是决定薄膜质量的重要指标之一。研究表明,工作气体浓度、工作气压、靶间距以及衬底温度等工艺参数设定的不同对膜层均匀性均产生很大的影响。衬底表面温度的高低会影响膜层的附着程度,衬底受热的均匀性对衬底表面膜层质量的一致性有影响[1-3]。因此,准确地测量并控制衬底温度是提高膜层质量的关键。
在大面积金刚石膜镀制过程中,采用单个温度传感器所得到的测量值只能反映衬底表面某点的温度,误差较大且不足以反映整个衬底表面的温度信息。采用多只传感器在不同点处同时进行测量并通过数据融合方法对测量数据进行处理,不仅能更全面地反映衬底表面温度,而且可以提高温度测量值的精度[4-5]。笔者随机在10个测量点安放热电偶温度传感器(以获得衬底表面温度实时数据),分别采用最优加权与最小二乘结合算法、最优加权与Bayes估计结合算法、最优加权与递推最小二乘结合算法对所测得的温度值进行融合研究,并对融合方法的稳健性进行比较分析。
1 温度测量数据的获取
将10只热电偶温度传感器随机安置在衬底表面不同位置,以同时对衬底表面温度数据进行实时采集。采用凌华科技多功能数据采集卡DAQ-2214,每隔0.2s采集一次温度,将5个温度值作为一组,表1给出了一组温度测量值。由于安装位置及离衬底表面距离的不同,温度测量值存在一定的误差,但其与真值700℃之间的误差均小于5℃。

表1 温度采样值 ℃
2 温度测量数据融合研究
采用10只温度传感器获得10个不同位置同一时刻的温度采样值,对温度采样值首先通过最优加权融合方法得出每一时刻的温度融合值。为了能够更好地滤除测量噪声,提高融合精度,将最优加权融合所得的5个温度融合值采用最小二乘法、Bayes估计法和递推最小二乘法进行第二次数据融合,得出温度测量值的最终融合结果,并对融合结果进行比较分析[6-7]。图1所示为大面积金刚石膜衬底温度测量数据融合模型。

图1 大面积金刚石膜衬底温度测量数据融合模型
通过对10只传感器同一时刻的温度测量值进行最优加权,将10只传感器同时刻测量值融合为一个值。任意温度测量值ti=t+Ki,其中,t为温度的真值,Ki为测量噪声。假设第i个传感器的测量值方差。加权值式中,n为传感器的个数;Wi为对应温度值的加权系数,

加权融合值的均方误差为

最优加权融合的权数可以转化为求W1,W2,…,Wn,使得均方误差最小,根据拉格朗日条件极值的求法,可得权系数

基于最优加权融合方法的温度融合结果示于表2。由各测量点温度测量值对应的权系数可看出,离真值700℃越远的数据对应的权系数越小,即对融合结果精度影响越小;同时可看出,5个最优加权温度融合值的精度均小于0.1℃。

表2 基于最优加权温度数据融合结果
2.1 基于最小二乘法温度测量数据融合
将通过最优加权融合法获得的一组温度融合值,通过最小二乘法进行再次融合从而获得更高精度的温度融合值。根据最小二乘法数据融合原理[8],温度融合值:
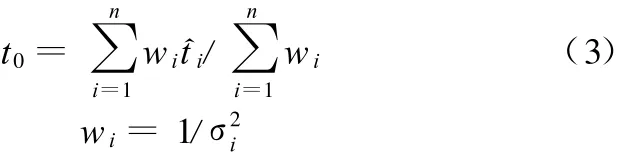
经过编程计算求得温度融合值t0=699.9947℃,与真值之间的误差小于0.1℃。
2.2 基于Bayes估计法的温度测量数据融合

经过编程计算,得出融合结果t0=699.9948℃。
2.3 基于递推最小二乘法的温度测量数据融合
根据递推最小二乘算法的递推关系[10]:

式中,Yn为第n次的温度融合值;n为第n次的温度最优加权融合值;Pn为中间加权量。

表3 基于递推最小二乘法的温度数据融合结果
2.4 融合结果分析
将以上三种温度数据方法所得的融合结果及误差值列于表4。由表4可看出:基于最优加权与最小二乘结合法(OWLS)、最优加权与Bayes估计法(OWBE)所得的融合值精度更高,融合值与真值之间的误差小于0.01℃,能够更好地剔除测量过程中出现的各种噪声,逼近真值;基于最优加权与递推最小二乘法(OWRLS)的温度数据融合结果的精度控制在0.1℃以内。

表4 温度融合结果比较 ℃
3 融合方法稳健性分析
为了对三种融合方法的稳健性进行比较[11],在MATLAB软件编程实现上述数据融合算法程序[12],考察温度测量受各种扰动时所得的融合结果变化情况。
3.1 单一温度测量数据受扰动
当某只传感器的某次测量受到某种扰动时,其测量值将会偏离真值;如果测量回路出现断线、短路等故障时,传感器的当前测量值会发生突变,即跳变成零或传感器测量量程的上限值。
图2给出了某次温度测量的扰动量小于10℃时,由三种融合方法所得融合结果随温度扰动值变化关系的曲线,其中,tij为第i只传感器第j次温度测量值,trh1为温度融合值。图2中,OWLS、OWBE的融合结果十分接近,波动小;OWRLS对应的融合结果波动较大,其与真值之间的误差较大。因此,在温度测量扰动量较小的情况下,OWLS、OWEB的温度数据融合方法稳健性佳,OWRLS的温度数据融合方法稳健性相对较差。

图2 单一温度测量受较小扰动融合结果
表5给出了单一温度值受较大扰动甚至温度测量值达到传感器量程上下限值时,三种不同融合方法所得的温度值。通过数据融合可看出,OWLS、OWBE融合结果精度更高,其融合方法的稳健性均可保证。

表5 单一温度测量值受较大扰动融合结果 ℃
3.2 多个温度测量数据受扰动
温度测量时有可能多个温度传感器在同一时刻会受到大小不一的扰动,从而导致不同温度测量值偏离真值的程度不同。由于扰动数据出现的随机性,为了分析的方便,不妨选取温度测量值t51、t44受到较小扰动(扰动量小于10℃)时对所测得温度数据进行融合分析。图3为t51、t44温度测量值在(691℃,709℃)范围变化时,融合结果trh2随扰动量变化的三维曲面图。
从图3可看出,温度融合值精度很高,即与真值之间的误差小于0.01℃,OWLS、OWBE的融合结果对应的曲面几乎为平面,融合方法的稳健性好,而OWRLS融合结果曲面的平整度相对较差,精度达到0.1℃,融合方法稳健性相对较差。
表6对多个传感器测量值发生较大扰动时所得的温度数据融合结果进行比较,仍可看出:OWLS、OWBE的融合结果十分近似,均能达到很高的精度,稳健性能佳;OWRLS融合结果的精度相对较差,稳健性能相对较差。

图3 多个传感器测量值受较小扰动融合结果曲面

表6 多温度测量值受较大扰动融合结果比较 ℃
4 结语
采用凌华数据采集卡获得了大面积金刚石膜衬底表面温度实时测量值,通过三种不同的数据融合方法经过两步数据融合获得了高精度的温度融合值;当温度测量受到各种不同扰动时,对温度融合方法的稳健性进行了比较分析。研究结果表明:通过两步数据融合可进一步提高温度测量值融合结果的精度;最优加权与最小二乘结合算法、最优加权与Bayes估计结合算法在受到各种大小不同的扰动时,融合结果的误差均小于0.01℃;最优加权与Bayes估计结合算法精度最高,最优加权最小二乘结合算法次之,最优加权递推最小二乘结合算法相对较差。通过比较分析可知,最优加权与最小二乘结合算法、最优加权与Bayes估计结合算法表现出非常好的稳健性,最优加权与递推最小二乘结合算法稳健性能相对较差。
[1]汉斯◦琼彻◦格雷瑟.大面积玻璃镀膜[M].上海:上海交通大学出版社,2006.
[2]May P W.Diamond Thin Films:a 21st-century Material[J].Phil.T rans.R Soc.Lond.A,2000,358(1766):473-495.
[3]吕反修.化学气相沉积金刚石膜的研究与应用进展[J].材料热处理学报,2010,31(1):15-28.
[4]Saporta G.Data Fusion and Data Grafting[J].Computational Statistics&Data Analysis,2002,38(4):465-473.
[5]王志胜,周军,周凤岐.异质传感器数据的最优线性融合[J].中国惯性技术学报,2002,10(5):50-53.
[6]Sinha A,Chen Huimin,Danu D G,et al.Estimation and Decision Fusion:a Survey[J].Neurocomputing,2008,71(13/15):2650-2656.
[7]孙勇,景博,张劼.最优加权与递推最小二乘法相结合的多传感器信息融合[J].传感技术学报,2004,17(4):630-632.
[8]刘建书,李人厚,常宏.基于相关性函数和最小二乘的多传感器数据融合[J].控制与决策,2006,21(6):714-716.
[9]吴小俊,曹奇英,陈保香,等.基于Bayes估计的多传感器数据融合方法研究[J].系统工程理论与实践,2000,20(7):45-48.
[10]Zhu Fengchun,Dai Ju.Multi-robot Fusion with Measurements Compensation Based on Recursive Least Square[C]//IEEE International Conference on Control and Automation.Guangzhou,2007:2953-2957.
[11]涂国平.多传感器数据融合的稳健处理方法[J].数据采集与处理,1998,13(1):85-87.
[12]张德丰.M ATLAB数值计算方法[M].北京:机械工业出版社,2010.

