基于遗传-蚁群算法的PHEB模糊控制策略优化

尹安东 赵 韩 张 辉

合肥工业大学,合肥,230009

0 引言

目前,混合动力汽车(hybrid electric vehicle,HEV)的控制策略主要有逻辑门限值控制策略、瞬时优化控制策略、全局优化控制策略和模糊控制策略等[1-2]。模糊控制策略鲁棒性强、实时性好,具有很强的实用性,但模糊控制策略隶属度函数和模糊控制规则的选取主要依靠专家经验,一般情况下无法获得全局最优,因此需要对模糊控制策略进行优化,以获得最优的控制性能。

HEV控制策略优化是复杂的非线性优化问题,很难用传统的一些优化方法来求解。近年来涌现出的智能优化方法,如遗传算法、蚁群算法和粒子群算法等,能够在搜索过程中自动获取和积累有关搜索空间的知识,实现在复杂空间中的有效搜索[3]。遗传算法(genetic algorithms,GA)是一种具有很强全局寻优能力的仿真算法,但未利用系统中的反馈信息,降低了求解效率[4-5];蚁群算法(ant colony algorithms,ACA)是一种新型的模拟进化算法,重点始于组合优化问题的求解,但存在收敛较慢的问题[6-7]。故笔者采用集遗传算法和蚁群算法优点的遗传-蚁群算法(geneticant colony algorithm,GACA),对并联式混合动力电动客车(parallel hybrid electric bus,PHEB)的混合动力系统模糊控制器的隶属度函数和模糊控制规则进行优化,并运用MATLAB/Advisor进行实例PHEB性能仿真分析。

1 PHEB模糊控制策略设计

1.1 PHEB混合动力系统工作模式分析

鉴于城市客车停靠站点多、车速不高、起步、停车十分频繁等特点,结合超级电容具有在短时间内可大电流充放电、循环寿命长、充放电效率高等优势,在传统燃油城市客车结构基础上,设计了一种超级电容和柴油发动机混合的并联式混合动力系统。鉴于超级电容的辅助动力作用,混合动力系统的发动机工作点范围可向其最佳燃油经济性曲线的上下两侧进行适当拓展,如图1所示的Ⅱ区域。为了充分发挥并联式混合动力系统的优势,PHEB在不同的行驶工况下,具有多种不同的控制模式:

(1)汽车在启动和低速行驶时,为避免发动机处在高油耗率区,由超级电容放电驱动电机,实现纯电驱动模式。

(2)当汽车在加速或爬坡等大负荷情况下,或发动机的工作点位于如图1所示的Ⅰ区域时,进入发动机和电机混合驱动模式。

(3)当汽车匀速行驶时,发动机单独驱动,并根据超级电容的荷电状态(state of charge,SOC)值来确定是否对其充电。若发动机工作在相对经济区间(Ⅱ区域),则超级电容不工作;若发动机的工作点位于如图1所示的Ⅲ区域,并且超级电容的SOC值低于预先设定的下限值,则发动机在提供整车所需功率的同时向超级电容充电,直到超级电容SOC值超过预先设定的上限值为止。

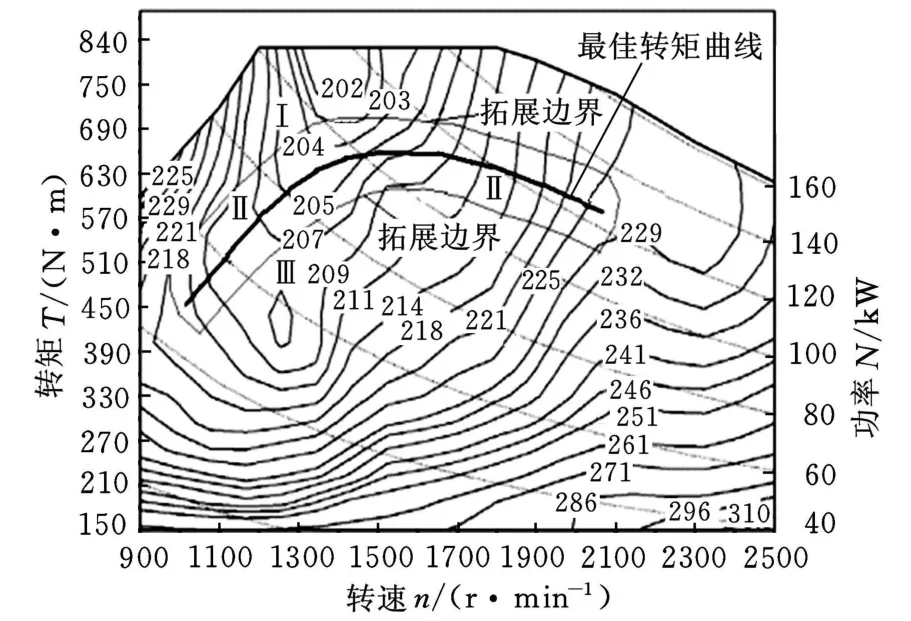
图1 发动机万有特性图

(4)汽车减速/制动时,电机作为发电机运转,把驱动轮的动能转化为电能,并通过功率转换器给超级电容充电,实现再生制动能量的回收。

1.2 PHEB模糊控制策略设计

1.2.1 模糊控制器的设计

鉴于PHEB混合动力系统结构特点,设计一种模糊控制器,结构如图2所示。该结构主要由3个模块组成:①转矩转化模块,计算整车的需求转矩与当前转速下发动机最优输出转矩的差值ΔT;②模糊推理模块,它是模糊控制器的核心部分[8],由两个输入量(整车需求转矩与发动机最佳转矩之差ΔT以及超级电容当前SOC值)和一个输出量(发动机输出转矩 T)构成;③转矩修正模块,根据模糊推理器的输出,最后转化为发动机的实际输出转矩Te。

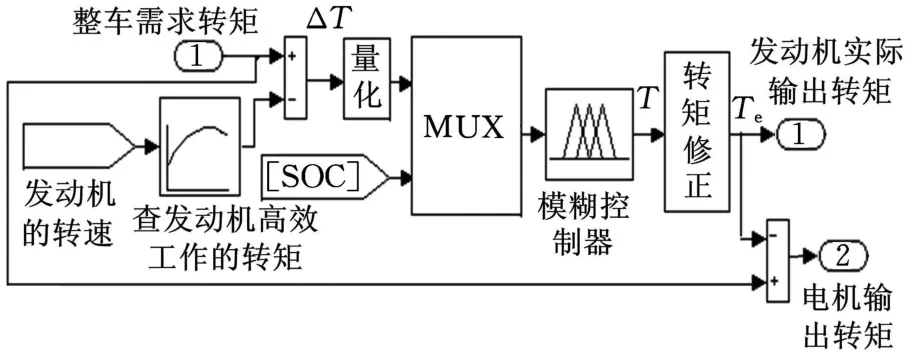
图2 PHEB模糊控制器结构示意图

1.2.2 隶属函数

输入变量ΔT和SOC的论域分别为[-3,3]和[1,7],输出变量 Te的论域为[1,7]。输入变量ΔT和SOC均定义为5个模糊子集,ΔT描述为{NB(负大)、NS(负小)、ZO(零)、PS(正小)、PB(正大)};SOC 描述为{S(小)、RS(较小)、M(中等)、RB(较大)、B(大)},输入变量 ΔT 和SOC 的隶属函数分别如图3和图4所示。根据发动机的效率曲线图,将输出变量 Te定义为7个模糊子集,Te描述为{VS(极小)、S(小)、RS(较小)、M(中等)、RB(较大)、B(大)、VB(极大)},输出变量Te的隶属函数如图5所示。

图3 输入变量ΔT的隶属函数

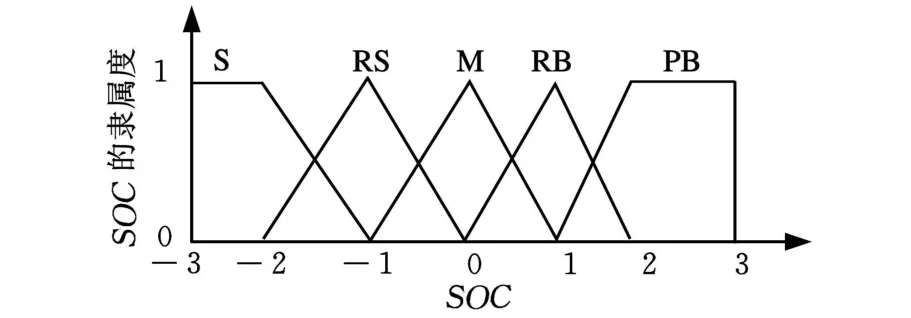
图4 输入变量SOC的隶属函数

图5 输出变量Te的隶属函数

1.2.3 模糊控制规则

模糊推理的规则建立原则是,在保证超级电容充放电平衡的情况下,尽量使发动机工作在最优曲线附近。在确定各输入、输出变量模糊子集和隶属度函数后,就可以列写出模糊控制规则,如表1所示。

表1 Te的模糊控制规则表

1.3 PHEB控制策略优化目标

PHEB优化目标就是在满足汽车动力性能的基础上,尽量使PHEB的等效燃料消耗量最小。PHEB控制策略优化问题是一个典型的非线性约束优化问题[9],其数学模型可以表述为

其中,F(x)为等效燃料消耗量;f(x)为优化目标函数,其约束条件 gr(x)(r=1,2,…,M)是一组非线性不等式约束,这里主要是满足PHEB的性能要求,即加速时间、最大爬坡度、0～50km/h的加速时间和超级电容组SOC的平衡等要求。针对实例PHEB的性能技术要求,约束条件设计如下:①最高车速g1(x)≥80km/h;②最大爬坡度g2(x)≥20%;③0～50km/h的加速时间g3(x)≤30s;④超级电容SOC初始值和终值之差g4(x)≤0.5%。

2 基于GACA的模糊控制策略优化

2.1 GACA的基本思路

鉴于遗传算法具有大范围全局搜索的能力,蚁群算法具有正反馈寻优等优点,采用集遗传算法和蚁群算法优点的GACA。GACA的基本思路是以PHEB等效燃料消耗量为优化目标,首先利用遗传算法产生较优解,并留下初始信息素分布;然后在有一定初始信息素分布的情况下,利用蚁群算法寻求最优解,充分发挥遗传算法与蚁群算法在寻优搜索中各自的优势。

2.2 遗传算法规则

2.2.1 编码以及群体初始化

采用浮点数编码方法进行编码,将优化问题的实际参数构成染色体编码。初始群体中的个体是随机产生的,通过编码随机产生 N个个体形成初始群体。

2.2.2 适应度函数

适应度函数可等价于蚁群算法过程中的目标函数,并将约束加入到适应度函数中[10]。

2.2.3 选择方法

采用最佳个体保留策略和赌盘轮法相结合的选择方法,即在群体交叉之前选出最佳个体,直接遗传到子代群体中,其余个体采用赌盘轮法来选择。

2.3 蚁群算法规则

2.3.1 信息素的初始值设置

通过遗传算法得到了一定的路径信息素,把信息素的初始值τS设置为

式中,τC为具体求解问题给定的一个信息素常数;τG为遗传算法求解结果转换的信息素值。

2.3.2 路径选择

在节点i的第k只蚂蚁选择下一跳节点j的规则:

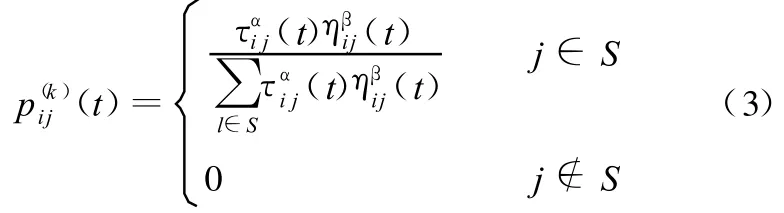
式中,τij(t)为t时刻在i、j连线上的信息素量;ηij(t)为与τij(t)对应的启发式信息;α、β分别为调节信息素强度τ和启发式信息η相对重要性的参数;S为蚂蚁可行路径节点集合(t)为t时刻第k只蚂蚁由位置i转移到位置j的概率。

2.3.3 信息素的更新

信息素的更新采用局部更新和全局更新相结合的策略。局部更新可避免蚂蚁在上次更好的路径有限相邻区域内搜索,全局更新对历史最优解路径上的信息素进行更新。当第k只蚂蚁成功地完成从i到j的一跳,信息素按照式(4)进行更新:

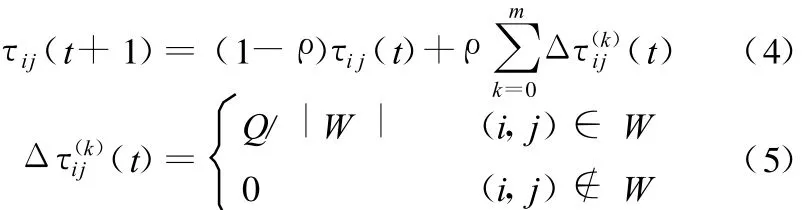
当所有的蚂蚁完成了一次循环后,选择出目标函数值最小的路径,再按照式(6)进行全局信息素更新,以达到较快收敛于最优解的目的:

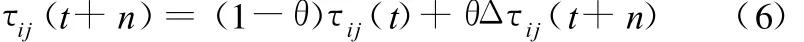
式中,θ为全局信息素挥发系数,0≤θ＜1;Δτij(t+n)为蚁群完成一次循环后的信息素修改值。

2.4 GACA优化流程

基于GACA的控制策略优化流程如下:①随机产生1组实数编码;②根据遗传算法进行若干次迭代,依据目标函数,生成初始信息素分布;③根据式(3)初始信息素分布,在源节点放置m只蚂蚁,每只蚂蚁依据状态转移概率选择下一跳节点;④蚂蚁完成一步后,根据式(4)进行局部信息素更新;⑤所有的蚂蚁完成1次循环后,根据式(6)进行全局信息素更新;⑥若满足结束条件,即循环次数Tc≥Tmax则循环结束并输出最优解,否则跳转到步骤 ⑤。

2.5 基于GACA的PHEB模糊控制策略优化

将GACA和模糊控制相结合,利用GACA优化PHEB模糊控制器的隶属函数和模糊控制规则,以期得到最优的模糊控制策略。在已设计的PHEB模糊控制器(图2)的基础上进行GACA优化,建立优化模型,如图6所示。通过GACA对已建立的糊控制器的控制变量进行调整优化,从而得到最优的两个输入控制变量(整车需求转矩与发动机最佳转矩之差 ΔT、超级电容当前SOC值)以及一个输出控制变量(发动机的实际输出转矩Te)的隶属函数和模糊控制规则。

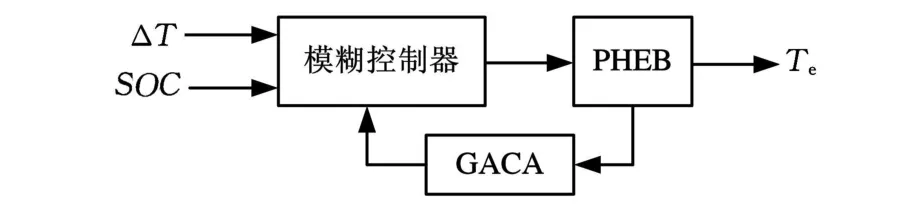
图6 基于遗传-蚁群算法的控制策略优化模型

3 基于实例的PHEB模糊控制策略优化

3.1 实例PHEB主要技术参数

实例PHEB车型是在传统燃油城市公交车基础上改装而成的,采用由超级电容和柴油发动机组成并联式混合动力系统。根据城市公交车的运行状况以及道路条件,确定实例的PHEB主要参数,如表2所示。

表2 PHEB主要技术参数表

3.2 基于Advisor的实例PHEB仿真模型建立

首先利用MATLAB/Simulink建立发动机、电机、超级电容等主要部件的仿真模型,并在Advisor平台上进行整车模型的二次开发。然后在MATLAB/Simulink环境下建立基于GACA的模糊控制模块,并嵌入到Advisor整车仿真模型中,得到整体封装后的基于GACA模糊控制策略的PHEB整车仿真模型,如图7所示。其中,优化后的模糊控制模块的输入控制变量ΔT和SOC及输出控制变量Te的隶属度函数分别如图8～图10所示。

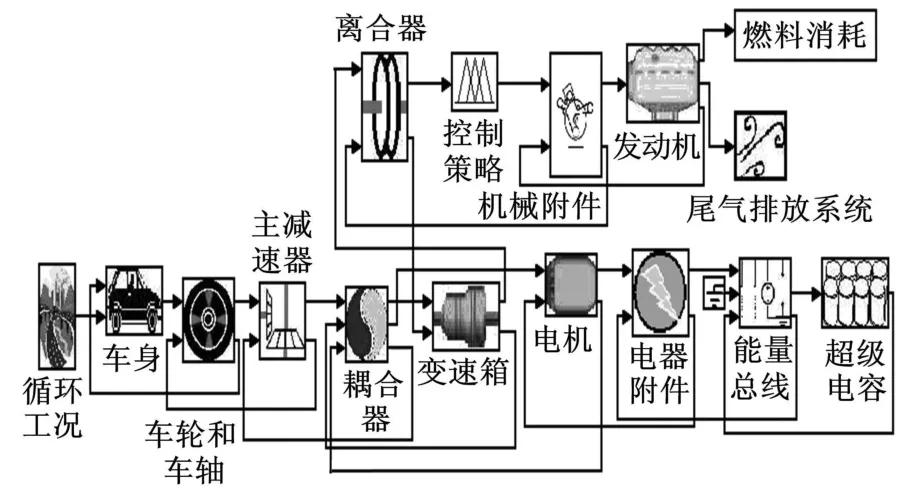
图7 基于GACA的模糊控制策略优化的PHEB整车仿真模型

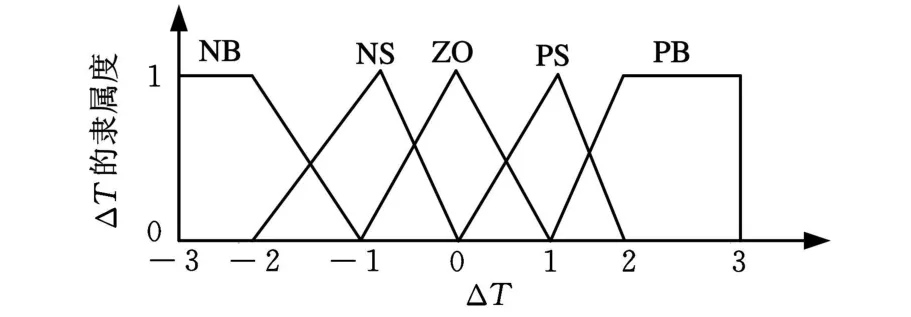
图8 优化后的输入变量ΔT的隶属函数

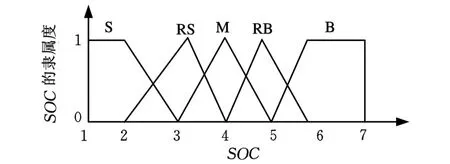
图9 优化后的输入变量SOC的隶属函数

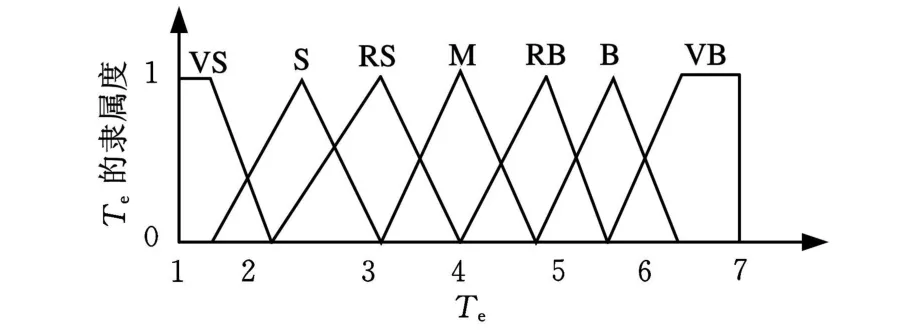
图10 优化后的输出变量Te的隶属函数

3.3 实例PHEB仿真结果分析

在基于GACA模糊控制策略优化的PHEB整车模型(图7)中,输入实例PHEB基本数据(表2),在中国典型城市公交循环工况下进行仿真分析[11]。结果表明:与优化前相比,优化后的发动机工作点控制在效率较高的区域内(图11),且超级电容SOC值的变化控制在较小的范围内(图12)。

3.4 实例的PHEB道路测试结果分析

基于GACA优化的模糊控制策略,经硬件在环验证试验,并与实例PHEB实车道路测试结果进行比较,结果及分析如表3所示。表3中,误差表示优化后的仿真值与实车测试值的相对误差。

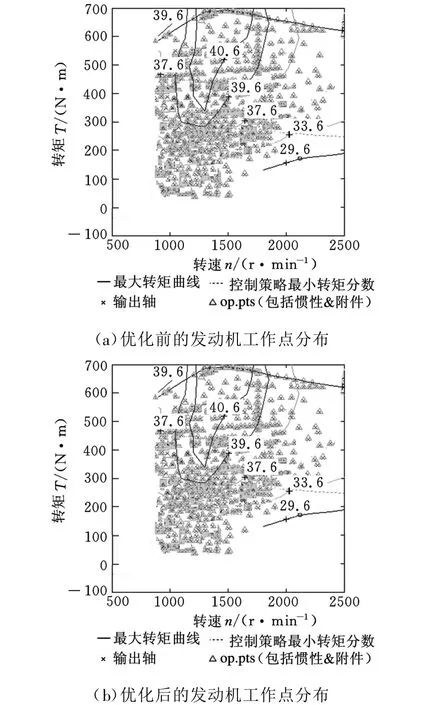
图11 基于Advisor的发动机工作点的分布

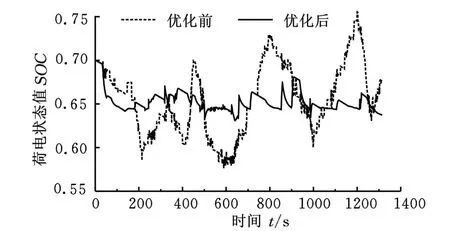
图12 基于GACA优化前后S OC值变化曲线

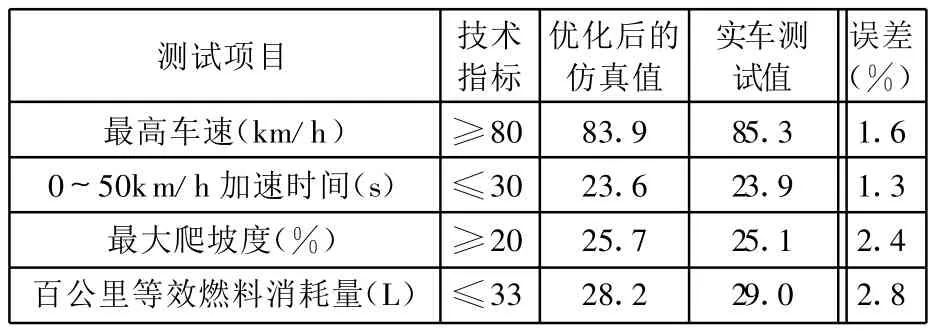
表3 优化后的仿真值与测试值比较

实例PHEB测试结果表明:基于GACA优化的模糊控制策略能够满足整车动力性能指标要求;优化后百公里的等效燃料消耗量仿真值为28.2L,比优化前百公里的等效燃料消耗量仿真值31.4L降低了10.2%;实车测试的百公里等效燃料消耗量为29.0L,比同类车型的传统燃油客车的百公里燃料消耗量36.2 L降低了19.9%;与实车测试值相比,优化后的各项指标仿真值的相对误差均小于3%。

4 结论

(1)基于超级电容的PHEB动力系统的结构特点,设计了分别以整车需求转矩与发动机最佳转矩之差值以及超级电容荷电状态为输入,以发动机转矩为输出的模糊控制器。采用集遗传算法和蚁群算法优点的GACA,对PHEB的混合动力系统模糊控制器的隶属度函数和模糊控制规则进行优化。

(2)实例PHEB仿真分析和实车道路测试表明:基于GACA优化的模糊控制策略能将PHEB的发动机控制在最佳燃油经济性曲线附近,且超级电容SOC值的变化在较小的范围内;在满足动力性能指标要求的情况下,基于GACA优化的PHEB等效燃料消耗量的仿真值比优化前降低了10.2%;实车测试的百公里等效燃料消耗量比同类车型的传统燃油客车的百公里燃料消耗量36.2L降低了19.9%,从而验证了基于GACA优化的模糊逻辑控制策略的可行性,为新能源汽车的混合动力系统控制策略设计和优化提供了一种新途径。

[1]陈清泉,朱家琏,田光宇.现代电动汽车技术[M].北京:北京理工大学出版社,2007.

[2]Farzad R S.Control Strategies for Hybrid Electric Vehicles:Evolution,Classification,Comparison,and Future Trends[J].IEEE T ransactions on Vehicular Technology,2007(5):2393-2404.

[3]吴剑.并联式混合动力汽车能量管理策略优化研究[D].济南:山东大学,2008.

[4]Morteza M G,Amir P,Babak G.Application of Genetic Algorithm for Optimization of Control Strategy in Parallel Hybrid Electric Vehicles[J].Journal of the Franklin Institute,2006,343(4/5):420-435.

[5]朱传高.并联混合动力汽车遗传模糊控制策略的优化研究[D].长春:吉林大学,2009.

[6]赵义武,牛庆银,王宪成.遗传算法与蚁群算法的融合研究[J].科学技术与工程,2010,10(16):4017-4020.

[7]刘彦鹏.蚁群优化算法的理论研究及其应用[D].杭州:浙江大学,2007.

[8]资新运,杜常清,张增建,等.混合动力汽车模糊逻辑转矩管理策略仿真混合动力汽车模糊逻辑转矩管理策略仿真[J].武汉理工大学学报,2008,30(4):561-564.

[9]吴静波,张承宁,邹渊,等.基于遗传蚁群算法的履带式混合动力车辆控制策略参数优化[J].车用发动机,2009(3):44-48.

[10]浦金欢,殷承良,张建武.遗传算法在混合动力汽车控制策略优化中的应用[J].中国机械工程,2005,16(7):648-652.

[11]中国国家标准化管理委员会.GB/T 19754-2005.重型混合动力电动汽车能量消耗量试验方法[S].北京:中国标准出版社,2005.