基于OFDM的认知无线电系统中功率分配算法

杨守义，宋延涛，陈泽先，陆彦辉

(郑州大学信息工程学院，河南郑州450001)

0 引言

随着无线通信技术的迅速发展，对无线频谱资源提出来更高的要求，无线频谱资源贫乏的问题日益严重，已经成为制约无线通信技术未来发展的主要瓶颈之一.美国联邦通信委员会(Federal Communications Commissions：FCC)一份报告表明，许多授权频段在时域和空域都没得到充分的利用［1］.因此，美国联邦通信委员会(FCC)和其他频谱管理机构考虑在已有的授权频谱中引入其他的用户，且不会对授权频带内的用户造成不可接受的干扰，即实现机会频谱接入(Opportunistic Spectrum Access：OSA)技术［2］.

由于大多数无线频谱资源已经被授权分配，目前最大的挑战是如何在不影响授权用户传输的前提下共享频谱资源.MITOLA［3］在软件无线电技术的基础上提出认知无线电技术.认知无线电技术作为一种新兴的无线通信系统，旨在对空、时、频等各域上的空闲资源(亦称为“频谱空洞”或“白色空间”)进行有效的感知探测和合理的再利用［4］，其主要作用是在不影响授权用户(License User：LU)正常通信的前提下，寻找频谱机会进行认知用户(Cognitive User：CU)间的有效通信，可以说认知无线电技术是目前解决频谱资源匮乏的最有效方法［5］.

正交频分复用(Orthogonal Frequency Division Multiplexing：OFDM)技术具有便于自适应调整参数，可重配的子载波结构，其接收端的快速离散变换模块也可同时用于频谱感知.抗多径干扰与频率选择性衰落能力强，频谱利用率高等优点，这些优点使得OFDM成为实现认知无线电系统的理想备选技术之一［6］.功率分配不仅是传统OFDM系统中的关键技术，而且还是认知无线电技术中频谱分析和判决的重要手段，在认知网络中链路容量最大化的同时也要深化功率分配研究.

笔者在文献［7］的基础上，通过对CU频带内子载波功率泄露对LU的干扰分析，在满足LU干扰约束的前提下，使认知用户频带内子载波分配的功率呈现幂函数分布，最大化CU频带内信道容量，并将其与文献［7］提出的方案进行比较.

1 系统频谱模型

考虑认知无线电系统的下行链路，一个基站给LU和CU同时提供服务，根据文献［8］中提到的OFDM调制子载波的IEEE 802.11a系统模型，假定提供给CU接入的空闲频带与LU频带的分布情况如图1所示.

图1 LU与CU共存的频谱模型Fig.1 LU spectrum model of coexistence with the CU

假设LU的信道带宽为B，CU频带的两侧均被LU频带占用，且CU频带内每个子载波的间隔，以及CU频带与LU频带的间隔均为Δf.由于CU和LU均采用OFDM调制方式(功率谱密度旁瓣的衰减特性)，因此，LU频带内将受到CU的干扰，同时CU频带内也将受到LU的干扰.

研究的内容是在保证CU对LU产生的干扰功率在同时满足对左、右两边LU频带的干扰功率约束的条件下，对CU频带内的子载波进行最优功率分配，以实现CU频带的信道容量最大化.

2 系统数学模型

CU对LU的干扰大小取决于CU频带内各个子载波上所需的发射功率，以及CU频带内各个子载波与LU频带间的最近频谱距离［8］.

2.1 CU对LU的干扰

假设CU频带中的第i个子载波上信号的功率谱密度为

式中：Pi表示CU频带中第i个子载波上的发射功率;Ts表示OFDM的符号周期;则CU频带中第i个子载波上的信号对LU产生的干扰功率为

式中：di表示CU频带中第i个子载波与LU频带间的最近频谱距离.

2.2 LU对CU的干扰

LU信号对CU频带中第i个子载波的干扰功率为

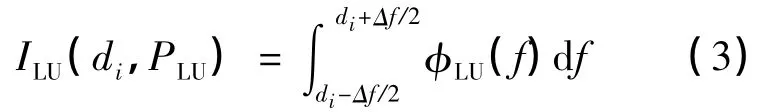
式中：φLU(f)表示LU信号的功率谱密度;PLU表示LU信号的功率.

2.3 CU 的传输速率分析［7］

假设所有子载波信道特性均服从瑞利衰落，且CU的每个子载波已获得相应的信道增益.CU频带中第i个子载波的传输速率Ri可表示为

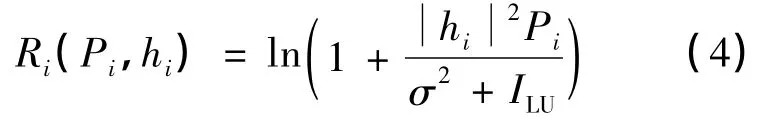
式中：hi表示CU频带中第i个子载波上的信道增益;σ2表示信道噪声方差.

3 功率分配算法

3.1 最优功率分配方案

最优化目标是CU频带中第i个子载波的信号对LU产生的干扰功率总和，在不大于左、右两边LU的干扰门限条件下，使CU频带中的传输速率最大化，即得到CU的信道容量［7］.

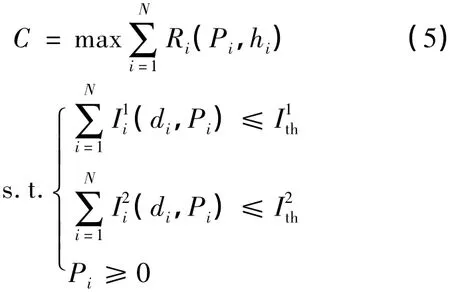
此时，最优化问题便演变成一个线性约束的凸优化问题，这一问题可以通过常用的数值方法来求解，利用Lagrange乘子法得

式中：λ1，λ2表示 Lagrange乘子.

对式(6)求导可得

将式(7)右边等于零，即得到Pi的最优解：

式中：(x)+=max{0，x}，而 λ1，λ2可由式(9)得到：

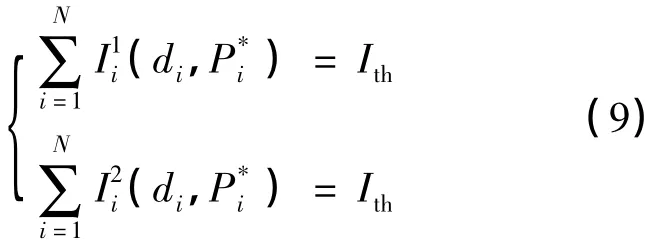
由(8)式可知，CU频带中第i个子载波被分配的功率，有可能出现小于零的情况，因此这里采取迭代分块注水(IPW)算法进行分析处理，经过多次迭代运算，直至CU频带中每个子载波所分配的功率是非负值为止［9］.

3.2 次优功率分配方案

在次优功率分配方案中，需要将CU频带内的子载波序号进行调整，自左向右序号依次为1，2，3，…，…，3，2，1，这里取 N 为偶数;当 N取奇数时，也有类似表述.鉴于文献［7］提出的次优化方案A和方案B，笔者提出了基于幂函数分布的方案C和方案D.

3.2.1 方案C(幂函数分布1)

该方案考虑CU频带内子载波所分配的功率，随着CU频带中子载波与LU频段之间频谱距离的增加，呈幂函数幅值特性阶梯状分布，我们假设第i个子载波分配的功率为

结合式(9)可得

3.2.2 方案D(幂函数分布2)

该方案考虑功率分配类似方案C，我们假设第i个子载波分配的功率为

结合式(9)可得

4 性能仿真与分析

在仿真与分析过程中，将最优化功率分配方案和各种次优化功率分配方案进行比较.利用文献［7］中给出的参数进行性能的仿真与分析，CU频带内的子载波总数 N=10，Ts=4 μs，B=0.312 5 MHz，Δf=0.312 5 MHz=1 μW，hi依次为1.235 2，0.257 2，0.799 2，0.602 9，0.744 5，1.301 7，1.549 0，1.422 8，0.499 5，0.829 0 dB.

图2给出了干扰门限值为2.4 μW时各种方案的功率分布柱状图，在最优方案中，CU频带内各个子载波上分配的功率呈现阶梯状分布，且是从两侧向中心依次递增，这是由于LU分别位于CU频带的两侧造成的结果.在其他方案中，CU频带内各个子载波上分配的功率均呈现左右对称分布，这是由于两边LU的干扰门限值相同导致的，同时也验证了笔者所提出的次优方案是合理的.

图2 不同方案的功率分布柱状图Fig.2 The power distribution histogram of different options scheme

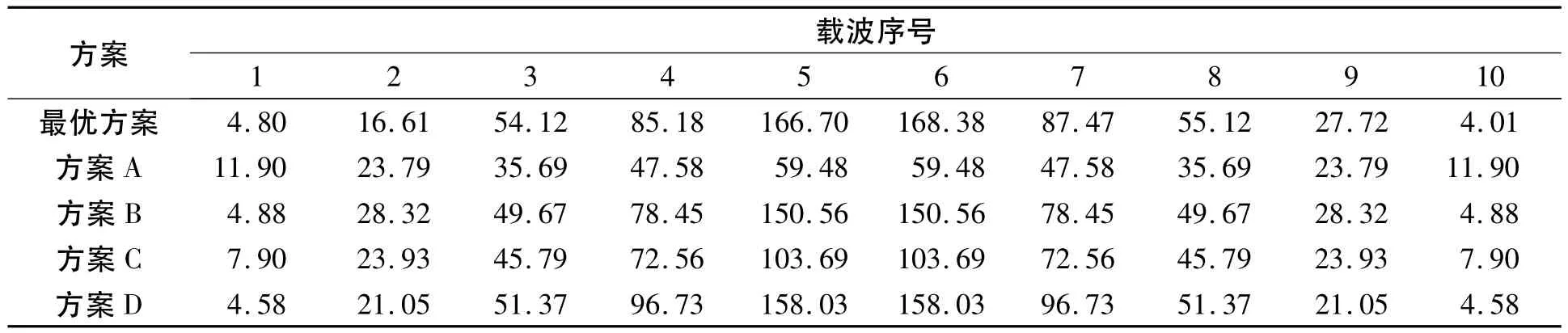
表1 不同方案的功率值Tab.1 The power values of different options scheme μW

表1给出图2中所分配功率的具体数据，从各种次优方案的子载波功率分布数据情况可知，方案D的分布最接近最优方案，方案B、C次之，方案A最差.

图3给出了不同干扰门限下CU的最大传输速率(其中小图为局部放大图).可以看出，其中方案D最接近最优方案，方案B、C次之，方案A最差.随着LU的干扰门限值的逐渐增加，方案D的最大传输速率向最优方案逐渐逼近.

图3 不同干扰门限下CU的最大传输速率Fig.3 Under different interference threshold of the maximum transmission rate of CU

图4给出了不同干扰门限下CU的最大发射功率.其中，在各种次优方案下，CU所得到的最大发射总功率中，方案D最接近最优方案，方案B、C次之，方案A最差.随着LU的干扰门限值的增加，方案D的最大发射总功率向最优方案逐渐逼近.

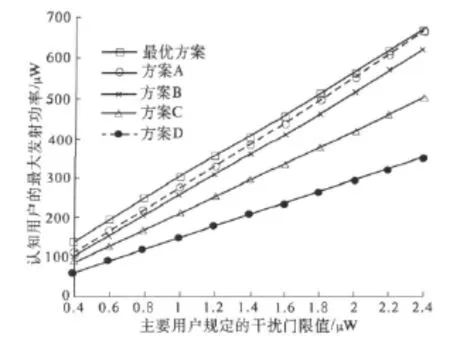
图4 不同干扰门限下CU的最大发射功率Fig.4 CU under different interference threshold of the maximum transmit power

在上述同样参数设置条件下，按照CU频带内子载波的功率分配呈现幂函数分布的方案，来比较不同幂指数条件下的最大传输速率.幂指数依次为：1.0，1.4，1.8，2.2，2.6，3.0.

图5 不同幂指数方案下的最大传输速率Fig.5 A power scheme under different maximum transmission rate

图5给出了不同幂指数方案下的最大传输速率(其中两个小图为局部放大图).当LU的干扰门限值Ith＞1.075时，指数为2.2的次优方案最大传输速率最接近最优方案;当LU的干扰门限值0.5≤Ith≤1.075时，指数为2.6的次优方案最大传输速率最接近最优方案，并且非常接近D方案;当LU的干扰门限值Ith＜0.5时，指数为3.0的次优方案最大传输速率最接近最优方案，并且非常接近D方案.

由此可以看出，在整个干扰门限值区间上，指数为2.2时的幂函数功率分布方案是一种折中的方案，验证了我们设计的次优方案D的合理性.

5 结论

笔者研究了基于OFDM的认知无线电系统中功率分配问题，指出在满足LU干扰门限的前提下，最大化CU频带内信道容量的次优化功率分配方案，可以通过求解一个凸优化问题获得.笔者对不同方案的功率柱状分布图，最大传输速率和发射功率这两性能指标，以及不同幂指数条件下最大传输速率进行了比较，结果表明笔者提出的次优化方案D是优于文献［7］提出的次优化功率分配方案.未来可进一步考虑在LU和CU频带间设置保护频带条件下，利用笔者提出的次优方案来进一步研究.

［1］FCC.Federal Communications Commission Spectrum Policy Task Force［R］.New York;FCC Report of the Spectrum EfficiencyWorkingGroup， November，2002.

［2］ZHAO Q，SADLER B.A survey of dynamic spectrum access：signal processing，networking，and regulatory policy［J］.IEEE Signal Processing Magazine，2007，55(5)：2294-2309.

［3］MITOLA J.Cognitive radio：making software radios more personal［J］.IEEE Personal Communications，1999，6(4)：13-18.

［4］SVENSSON C.Software Defined Radio-Vision or Reality［C］//24th Norchip Conference，2006：149-149.

［5］AKYILDIZ I F，LEE W，VURAN M C，et al.Next generation，dynamic spectrum access，cognitive radio wireless networks，a survey ［J］.Computer Networks，2006，4(8)：2127-2159.

［6］WEISS T，JONDRAL F.Spectrum pooling：An innovative strategy for the enhancement of spectrum efficiency［J］.IEEE Communications Magazine，2004，42(3)：S8-S14.

［7］BANSAL G，HOSSAIN M J，BHARGAVA V K.A-daptive power loading for OFDM-based cognitive radio systems［C］//Proc IEEE ICC，Washington DC：IEEE Press，2007：5137-5142.

［8］WEISS T，HILLENBRAND J，KROHN A，et al.Mutual interference in OFDM-based spectrum pooling systems［C］//Proc IEEE Vehicular Technology Conference Spring，IEEE Press，2004：1873-1877.

［9］WANG P，ZHAO M，XIAO L，et al.Power allocation in OFDM-based cognitive radio systems［C］//Proc IEEE Global Communication Conference，Washington DC：IEEE Press，2007：4061-4065.