基于最小一乘准则的GM(1,1)模型边值分析
刘卫锋,何 霞
(郑州航空工业管理学院 数理系,郑州 450015)
0 引言
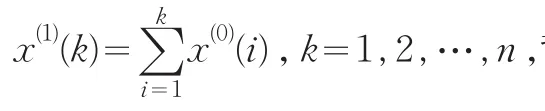
由GM(1,1)模型的白化微分方程可知,GM(1,1)模型的精度与参数a,u有着极大的关系,为此,文献[1-6]对如何确定a,u作了研究.而文献[7]通过对生成序列预测值x(1)(k),原始序列预测值x(0)(k)的表达式进行分析,发现边值条件的处理直接关系到预测效果,从而给出了边值修正形式x(1)(1)=x(0)(1)+b,其中b为修正项.同时给出了使用均方误差和最小准则确定边值修正的计算方法,即
准则Ⅰ 选取b,使得生成序列新预测值的误差在最小二乘意义下最小,即
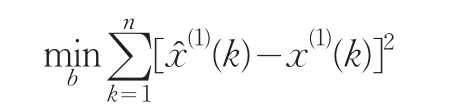
准则Ⅱ 选取b,使得原始序列新预测值的误差在最小二乘意义下最小,即
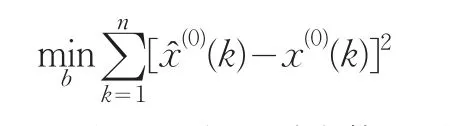
显然这两个准则皆使用最小二乘准则来确定边值修正项b,但是文献[8]指出,在最小二乘准则下,异常数据的误差会得到放大,从使得稳健性较差,并且在理论上加以证明,这说明了文献[7]中确定边值修正项的两个方法并不是理想的准则。
为此,本文提出将上述基于最小二乘的两个准则改为稳健性较好的最小一乘准则,从而得到基于最小一乘准则的确定边值修正项的灰色GM(1,1)模型.同时,本文给出了基于最小一乘准则的确定边值修正项的LINGO程序,从而使得计算极易实现.最后,本文的计算实例表明,基于最小一乘准则求解边值修正项的可行性与有效性,从而拓展了灰色GM(1,1)模型的适用范围。
1 基于最小一乘的边值修正项确定
1.1 边值修正项确定准则
针对生成序列和原始序列,选取稳健性较好的最小一乘准则来确定边值修正项.
准则1选取b,使得生成序列新预测值的误差在最小一乘意义下最小,即
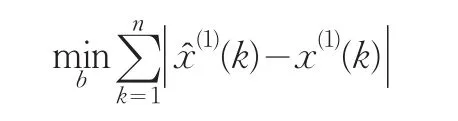
准则2选取b,使得原始序列新预测值的误差在最小一乘意义下最小,即
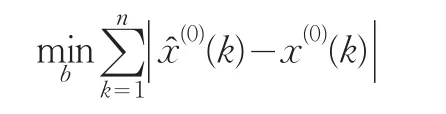
1.2 边值修正项确定的LINGO程序
尽管利用最小一乘准则确定边值修正项具有较好的稳健性,但是求解最小一乘问题确实一个难点,为此,我们使用LINGO程序来确定边值修正项.
基于准则1的LINGO程序:

2 计算实例
仍然选择文献[7]中全国电视机产量作为研究对象.原始数据为X(0)=(3.23,6.94,10.07,17.70,18.13,20.05,48.77,132.14,247.92,517.40,553.74)。
现根据准则1和准则2两种情况来求解修正项b,进行GM(1,1)模型分析。
第一种情况,以准则1求出边值修正项b=-27.04774,还原值为x(0)(k)=4.75039e0.482(k-1)。
第二种情况,以准则1求出边值修正项b=-27.78898,还原值为x(0)(k)=4.46690e0.482(k-1)。
现将根据准则1和2得到的GM(1,1)模型计算结果与文献[7]中根据准则Ⅰ和Ⅱ及传统GM(1,1)模型的计算结果列入表1进行对比.
表1计算结果显示,使用文中的两个最小一乘准则得到的模型的平均相对误差均比传统GM(1,1)模型和两个基于最小二乘准则建立的GM(1,1)模型大大降低,同时最大相对误差也均比传统GM(1,1)模型和两个基于最小二乘准则建立的GM(1,1)模型有所降低,这说明了最小一乘准则确定边值修正项比最小二乘准则有一定的优势。
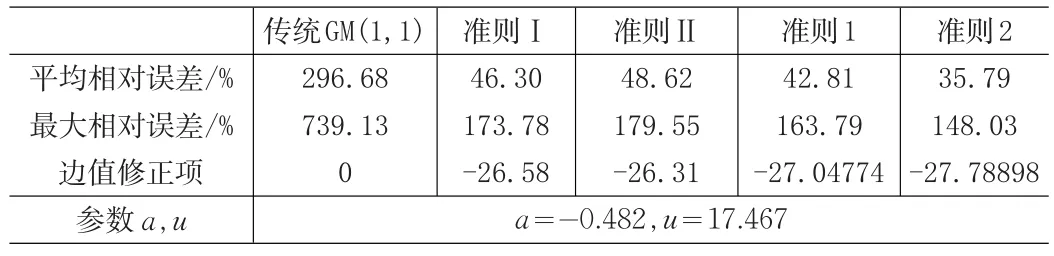
表1 模型计算结果比较
3 结语
(1)使用最小一乘准则计算灰色GM(1,1)模型的边值修正项,建立了具有较好稳健性的灰色GM(1,1)模型,提高了灰色GM(1,1)模型的精度,拓广了灰色GM(1,1)模型的适用范围。
(2)给出了基于最小一乘准则的边值修正项的LINGO程序,使得边值修正项的求解易于实现。
(3)计算实例表明,基于最小一乘准则的边值修正项的灰色GM(1,1)模型具有更高的精度,从而说明了最小一乘准则确定边值修正项的可行性与有效性,同时也说明了最小一乘准则比最小二乘准则有一定的优势。
[1]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.
[2]刘思峰,党耀国,方志耕等.灰色系统理论及其应用[M],北京:科学出版社,2010.
[3]庄恒扬.GM(1,1)建模机理与应用条件分析及其改进方法[J].系统工程理论方法应用.1993,2(3).
[4]罗荣桂,陈炜.灰色模型的一点改进及应用.系统工程理论与实践.1988,8(2).
[5]穆勇.灰色预测模型参数估计的优化方法[J].青岛大学学报.2003,16(3).
[6]田林亚,赵小飞,何习平.灰色模型GM(1,1)的稳健算法及其应用[J].吉首大学学报(自然科学版)2006,27(4).
[7]张辉,胡适耕.GM(1,1)模型的边值分析[J].华中科技大学学报.2001,19(4).
[8]冯守平.全最小一乘法[J].安徽大学学报(自然科学版).2009,33(3).

