允许订单延后的易腐品库存——路径问题研究
刘 静,贾 涛,吉 哲
(西安交通大学 管理学院,西安 710049)
0 引言
实物商品供应链内,企业运作管理的主要问题之一是如何达到供给与需求之间的平衡。除了调整运作能力之外,企业实际上常常通过影响需求的策略以达到匹配的目标,其中订单积压(延迟交货)是需求选择策略中有效的方法之一,从而在企业中有着广泛的应用。实物商品中,易腐品作为一大类产品与人们的生活紧密相关,例如蔬果海鲜、奶制品等,这类产品由于本身的物理特性等原因,其效用会随着时间的推移而改变,并产生额外的腐败成本。因而在易腐品库存管理中,引入订单延后策略不但能降低库存成本,还可以减少腐败损失,并通过优化缺货时间,权衡库存、腐败成本的减少以及缺货损失的增加,以提高供应链整体的运作绩效,从而具有理论和现实意义。
有关易腐品配送路径的问题,较多的出现在车辆路径问题(VRP)的研究中,例如Hemmelmayr等的血液配送问题。而在众多库存路径问题中,以易腐品为背景的还不常见,能综合考虑允许缺货的库存策略和配送路径网络的研究也比较少。在现实的易腐品分销渠道中,需求选择、库存控制和配送调度构成了运作计划体系的重要组成部分,因此,综合考虑易腐商品的订单延后、库存和配送路径决策,为一体化决策供应链的优化提供了另外一种选择。本文将以单一易腐品为对象,在一个供应商和多个零售商组成的供应链中,研究允许缺货的易腐品库存路径问题,通过模型构建证明目标函数的性质,以此为基础设计求解算法对问题进行求解;并结合数值算例说明实践中易腐品分销渠道内常见的成本权衡问题。
1 问题描述与符号假设
1.1 问题描述
本文研究的易腐品物流配送系统由一个供应商和N个零售商构成,供应商向零售商提供一种腐败率固定的易腐品,并定期为其补货。每个零售商拥有相互独立且固定的产品需求率。零售商允许缺货,所缺货物供应商会在下一个配送周期补齐。供应商送货的车辆同质且数目足够多,车辆具有最大载重约束。为了更加贴近物流管理实践,允许车辆在执行配送任务的过程中进行重复装货,每辆车在配送过程中行驶多个回路,负责一个区域的零售商的补货服务,最终每个零售商有且仅有一辆车为其服务。由于车辆行驶速度及最大载重量的约束,每个区域的配送周期以及每条回路的不缺货时间都有上下限。在无限计划期内,供应商在满足车容等约束的条件下,制定使得车辆固定成本、行驶费用、装卸费用、库存成本、腐败成本和缺货成本之和最小的合理的配送方案,确定对零售商的补货周期、补货量、零售商的不缺货时间以及车辆的行驶路径。
1.2 基本假设条件
(1)易腐品在零售商处由于销售条件的限制而存在常数腐败率,运输途中不发生腐败(采用冷链配送);
(2)配送过程中,货物装卸时间相对于运输时间和配送周期足够小,可以忽略不计;
(3)零售商无库存容量限制;
(4)一个周期中,每个零售商只接受一次补货服务。
1.3 符号表示
s:配送中心;S:零售商集合,S={1,2,…,i,…,N};S+:配送中心及零售商集合,S+=S⋃{s};V:车辆集合,V={1,…,v,…};Sv:车辆v服务的零售商集合;M:车辆v所行驶的路径集合,M={1,…,m,…};:车辆v第m次装货所服务的零售商集合;:车辆v第m次装货的装货量;σ:车辆行驶速度;ψ:车辆最大载重量;di:零售商i的产品需求率;φ:单次装卸费用;κ:单位时间车辆固定成本;δ:车辆单位路程行驶费用;θ:易腐品常数腐败率;p:单位产品腐败成本;h:零售商单位产品单位时间库存成本;b:单位缺货成本;tij:车辆从零售商i到零售商j的行驶时间;Tv:车辆v的配送周期;:车辆v行驶的第m个回路的周期,:配送周期Tv的取值上限和下限;:车辆v所行驶的第m个回路的周期上下限;ti:零售商i的不缺货时间:车辆v所行驶的第m个回路的不缺货时间;Ii(t):零售商i在t时刻的库存水平;Qi0:零售商i的期初库存水平;QiT:零售商i期末的缺货量;Qi:零售商i每周期的送货量;ICi,DCi,SCi:零售商i一个周期内的库存成本、腐败成本和缺货成本;ICv,DCv,SCv:车辆v所负责的补货服务单周期总库存成本、总腐败成本和总缺货成本;TCv:车辆v所负责的补货服务单位时间总成本。
2 模型构建
若车辆v负责某一区域零售商的补货服务,则该区域内所有的零售商的订货周期都相同,即为车辆v的配送周期Tv。该区域内的零售商i在周期Tv内,当0≤t≤ti时,库存水平为[12]:


由于在一条回路上零售商有相同的配送周期,因此在计算不缺货时间时,为了简化计算,本文采用了“按需求率等比例缺货原则”,即每个零售商的不缺货时间相同。
车辆v所服务的零售商集合Sv对应的单位时间库存成本可表示为:
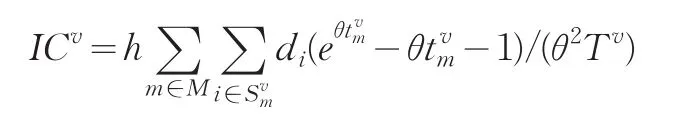
单位时间腐败成本为:

单位时间缺货成本为:
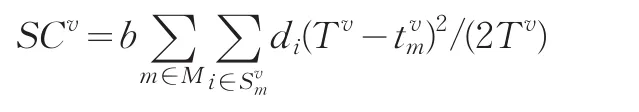
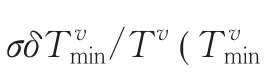
车辆v所负责的配送任务单位时间总成本=单位时间车辆固定成本+单位时间行驶费用+单位时间装卸费用+单位时间库存成本+单位时间腐败成本+单位时间缺货成本,可表示为:
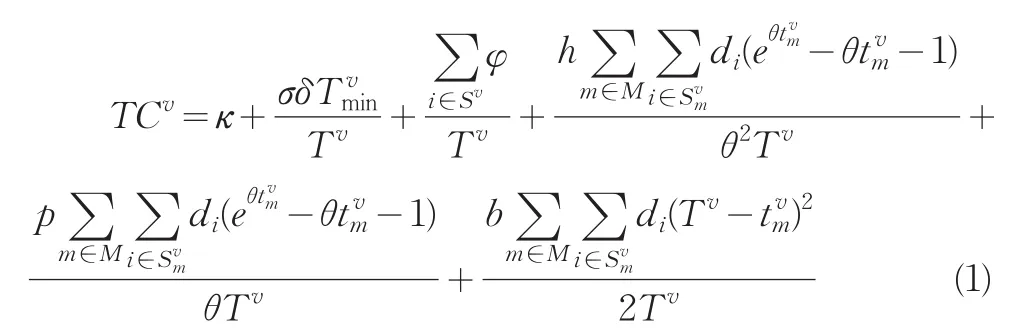
由表达式(1)可知,当车辆v的行驶路径确定后,单位时间总成本TCv与周期Tv以及各回路的不缺货时间tvm有关。

证明过程略。
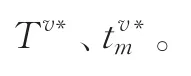
由于有多个车辆负责零售商的补货服务,系统总成本是由所有配送任务总成本之和构成的,为了得到单位时间系统总成本的表达式,本文又设置了如下变量:
:0-1变量,当车辆v从i行驶到j时否则变量,车辆v负责某一区域的零售商的补货服务时,yv=1,否则连续变量,车辆v第m次装货,从零售商i行驶到j的途中,该回路中还没有完成补货的零售商的补货量之和。
单位时间系统总成本的目标函数及约束条件如下:


上述模型是一个非线性规划模型。目标函数(2)表示无限计划期内,系统单位时间总成本;约束式(3)保证单周期内每个零售商有且只有一次补货服务;约束式(4)保证车辆v在行驶到一个零售商后,一定能离开此零售商,继续补货服务;约束式(6)表示对于任意的回路,不缺货时间不能大于配送周期;约束式(7)保证车辆v在驶入与离开零售商j时装载货物量之差等于零售商j要求的补货量;约束式(8)保证车辆v只有在执行配送任务时才能离开供应商;约束式(10)保证只有当车辆v从i行驶到j时,zmvij才不为零;约束式(11)是决策变量的取值范围。

3 求解算法
由上述模型可知,该问题目标函数复杂,且约束条件中包含非线性约束,求解过程中需要确定车辆行驶路径,即需要确定TSP回路,而TSP问题是运筹学中经典的NP-Complete问题,故该问题也是一个NP-Complete问题。因此,本节采用改进的节约算法这一启发式算法求解配送路径,并设计算法求解每条路径的周期和不缺货时间,进而求得每个配送任务的总成本。节约算法由Clarke和Wright提出并证明了其有效性,近年来被广泛的应用于求解车辆路径及其相关问题。与传统的节约算法不同的是,改进的节约算法除了满足车容量约束外,还要满足周期上下限的时间约束以及不缺货时间的约束,合并时并非以路径距离的减少值为节约值直接将两条回路合并,而是以配送任务总成本的减少值为节约值,先对车辆配送任务进行合并,再对每辆车所行驶的多个回路进行路径合并,改进的节约算法求解思路见算法1。由于路径确定后,成本函数与多个变量相关,故根据函数特点设计了算法求解配送周期和每条路径的不缺货时间,求解思路见算法2。
算法1:改进的节约算法求解路径
(1)初始化配送任务,每辆车负责一个零售商的配送,形成初始配送任务列表。
(2)两辆车的配送任务的合并。
①一辆车负责的配送任务包含n个回路,总成本为C1,另一辆车负责的配送任务包含m个回路,总成本为C2。将这两辆车所负责的配送任务合并,即合并后的配送任务包含n+m个回路(若此配送任务不可行,则放弃)。
②将①所得配送任务的n+m个回路视为一个回路列表,并对其进行路径调整。
a.用最近插入法[14]将回路列表中两条回路进行合并(若此合并不可行,则放弃),并记录其节约值(调用算法2)。
b.重复a,将所有可行的合并列出,并计算其成本节约值(调用算法2)。
c.记录b中节约值最大的合并。刷新回路列表,将由此合并得到的路径加入回路列表,并从回路列表中删除被合并的两条回路。转a,直到没有可行的回路合并为止,得到调整后的配送任务。
③记算②所得调整后的配送任务的总成本(调用算法2),并计算其合并节约值。
(3)重复(2),将所有可行的配送任务合并列出,并计算其成本节约值(调用算法2)。
(4)记录(3)中节约值最大的合并。刷新配送任务列表,将由此合并所得的配送任务加入配送任务列表,并从配送任务列表中删除被合并的两个配送任务。转(2),直到没有可行的配送任务合并为止,得到合并后的配送任务组合。
算法2:求解车辆v所负责的配送任务的周期、各回路的不缺货时间及总成本
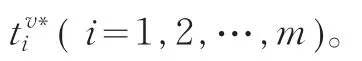
(2)判断Tv∗是否超界,并对Tv取值(若超界则取边界,若不超界则取最优周期),由约束式(9)求得在此Tv条件下每条回路的不缺货时间上界,并判断是否超界。
(3)若所有的都不超界,则将Tv和代入成本函数式(1)即得此配送任务的成本。针对每个超界的,依次将不缺货时间取为边界值,并带入成本函数式(1),并重新求解新的周期、其他回路的不缺货时间和此时的成本函数值(由式(1)确定,周期和不缺货时间超界则取边界)。
(4)返回(3)所得的配送任务成本的最小值,以及得出此最小成本的周期和各回路的不缺货时间。
根据命题1,各个不缺货时间的最优解虽然相同,但是由于约束式(9),不同回路的不缺货时间边界值可能不同,实际上根据算法2求得的各不缺货时间是可以不同的。
上述算法在Visual C++6.0平台上进行程序编写和运行,运行环境为:CPU—Inter®Core™2 Duo,2.0GHz,内存—2G,操作系统—Windows XP。
4 算例分析
基础数据来源于文献[9],有1个供应商给15个零售商配送一种腐败率固定的易腐品,相关基本参数为:车辆行驶速度σ=50千米/小时;车辆最大载重ψ=100吨;车辆单位时间固定成本κ=50元/小时;车辆单位路程行驶费用δ=1元/千米;零售商单位产品单位时间库存成本h=0.1元/小时*吨;单位缺货成本b=1元/小时*吨;单次装卸费用φ=50元;产品腐败率θ=0.03;单位产品腐败成本p=100元/吨;15个零售商的需求率分别为{0.109;0.326;0.322;0.478;0.134;0.429;0.381;0.503;0.187;0.123;0.953;0.638;0.247;0.188;0.441}。零售商及配送中心位置和距离矩阵见参考文献[9]。
求解结果为:供应商需要2辆车为零售商送货,第一辆车不重复装货,行驶路径为0-7-8-4-12-11-0,配送周期为33.86小时,路径不缺货时间为0.51小时,配送任务单位时间总成本为140.18元;第二辆车重复装货,行驶2条回路,路径为0-13-15-1-0-10-14-3-5-6-2-9-0,配送周期为55.31小时,第一条回路的不缺货时间为11.73小时,第二条回路的不缺货时间为11.73小时,配送任务单位时间总成本159.25元。单位时间系统总成本为299.43元。车辆行驶路径网络图1。
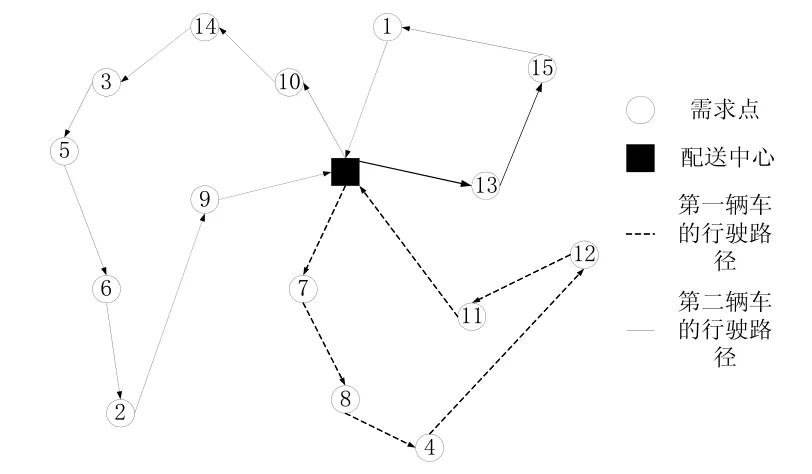
图1 车辆行驶路径网络图
当零售商处不允许缺货时,配送策略为:供应商共需要3辆车为零售商补货,第一辆车不重复装货,路径为0-15-1-14-10-0,配送周期为50.02小时,任务单位时间总成本为95.76元;第二辆车也不重复装货,路径为0-9-3-5-6-2-0,配送周期为38.2小时,任务单位时间总成本为114.16元;第三辆车重复装货,行驶2条回路,路径为0-7-8-4-0-13-12-11-0,配送周期为32.26小时,任务单位时间总成本为138.18元。单位时间系统总成本为348.1元。
以上测试结果表明,缺货策略会使系统总成本减小。这是由于在缺货状态下,不会发生产品腐败,客户需求量一定时,系统货运总量降低,对供应商的运输能力要求降低,因此供应商所需车辆数目减少,车辆固定成本减少,产品库存成本和腐败成本也减少。这两组测试说明,在不影响顾客需求的前提下,适当缺货会使供应链总成本降低,提高供应链整体效益。
5 结论
本文在现有易腐品允许缺货的库存问题和IRP问题研究的基础上,综合考虑易腐品供应链上的配送成本、库存成本、腐败成本和缺货成本,研究了两级供应链允许缺货的易腐品IRP问题,同时决策零售商的库存策略和配送策略。通过建立合理的数学模型,证明了当某一配送任务的路径确定后总成本与配送周期及各路径的不缺货时间等多个变量相关,且各路径在不考虑约束时的最优不缺货时间都相等。证明了成本函数的性质,在解析分析的基础上,以改进的节约算法得到配送路径,结合变量的边界条件,设计算法求解配送周期和各路径的不缺货时间。以算例验证问题和算法的有效性,测试结果分析表明,允许零售商部分缺货,会明显提高供应链的整体利益。
本文的模型只考虑了零售商处的腐败及缺货,并没有考虑供应商处的生产及腐败问题,然而在现实中,若供应商对产品进行相应的处理、包装,则会改变产品的腐败率及配送方式,进而改变供应链的总成本。如何在考虑供应商生产的条件下,综合权衡配送成本、库存成本、腐败成本和缺货成本,决策最优的配送方式和运输路径,将是笔者进一步研究的方向。
[1]Yang H L.Two-warehouse Inventory Models for Deteriorating Items with Shortages under Inflation[J].European Journal of Operational Research,2004,(157).
[2]Rong M,Mahapatra N K,Maiti M.A Two Warehouse Inventory Model for a Deteriorating Item with Partially/Fully Backlogged Shortage and Fuzzy Lead Time[J].European Journal of Operational Research,2008,(189).
[3]Hou K L.An Inventory Model for Deteriorating Items with Stock-Dependent Consumption Rate and Shortages under Inflation and Time Discounting[J].European Journal of Operational Research,2006,(168).
[4]Lo S T,Wee H M,Huang W C.An Integrated Production-Inventory Model with Imperfect Production Processes and Weibull Distribution Deterioration under Inflation[J].International Journal of Production Economics,2007,(106).
[5]Federgruen A,Zipkin P.A Combined Vehicle-routing and Inventory Allocation Problem[J].Operations Research,1984,(32).
[6]Anily S,Federgruen A.One Warehouse Multiple Retailer Systems with Vihicle Routing Costs[J].Management Science,1990,(36).
[7]Viswanathan S,Mathur K.Integrating Routing and Inventory Decisions in One-Warehouse Multiretailer Multiproduct Distribution Systems[J].Management Science,1997,(43).
[8]Qu W W,Bookinder J H,Iyogun P.An Integrated Inventory-Transportation System with Modified Periodic Policy for Multiple Products[J].European Journal of Operational Research,1999,(115).
[9]Aghezzaf E,Raa B,Landeghem H.Modeling Inventory Problems in Supply Chains of High Consumpution Products[J].European Journal of Operational Research,2006,(169).
[10]Abdelmaguid T F,Dessouky M M,Ordonez F.Heuristic Approaches for The Inventory-routing Problem with Backlogging[J].Computers&Industrial Engineering,2009,(56).
[11]Hemmelmayr V,Doerner K F,Hartl R F,et al.Delivery Strategies for Blood Products Supplies[J].Operations Research,2009,(31).
[12]Ouyang L Y,Teng J T,Goyal S K,Yang C T.An Economic Order Quantity Model for Deteriorating Items with Partially Permissible Delay in Payments Linked to Order Quantity[J].European Journal of Operational Research,2009,194(2).
[13]Clarke G,Wright J W.Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J].Operations Research,1964,(12).
[14]卢开澄.图论及其应用[M].北京:清华大学出版社,1981.
——基于集成射频识别技术

