基于模糊识别和神经网络的电网覆冰长期预测方法
宋尖,陆佳政,李波,张红先,徐勋建
(1.长沙理工大学,湖南长沙 410114;2.国家电网公司输变电设备防冰减灾技术重点实验室,湖南长沙 410007)
2008年我国发生了罕见的雨雪冰冻灾害,导致国民经济和人民财产遭受了重大损失,其中湖南受灾严重〔1〕。随着全球气候变暖,持续低温、雨雪、冰冻等灾害性天气出现的概率将会增长〔2〕。因此,有必要研究电网覆冰的长期预报,使其能够更好地为湖南电网防冻融冰工作计划提供指导。电网覆冰的长期预报时空尺度大、影响因素多,存在很大的不确定性,而人工神经网络能够很好地处理非线性、模糊性和不确定性关系的问题,本文采用误差反向传播算法的BP(Back Propagation)神经网络,结合湖南省往年的平均覆冰天数和气象历史数据,探讨湖南电网覆冰的长期预报。
1 预报因子的筛选
1.1 影响因子的选取
电网覆冰的形成与气象要素有密切的关系,而这些气象要素又受大气环流的支配〔3〕。将电网冬季覆冰现象之前的3—10月 (春夏秋季)的74项大气环流指数和4个湖南地面国际交换站的气温数据作为长期气象因子,并与湖南电网历史平均覆冰天数数据进行相关性分析,筛选出27个具有统计显著性的与湖南电网覆冰相关的影响因子。
其相关系数的计算公式为:

式中 xj,yj分别为气象因子和覆冰天数的历史值;¯x,¯y分别为xj,yj的平均值。
1.2 模糊识别的预报因子筛选方法
由于电网覆冰现象的影响因素多,且具有很大的不确定性,不少影响因子的物理意义尚不十分明确,如何从这些与预报对象相关性差异不大的众多影响因子中筛选出与覆冰现象最为密切的预报因子是值得深入探讨的问题。本文采用水文长期预报中的模糊识别方法来提取电网覆冰的长期预报因子。
根据模糊识别模型〔4-6〕,假设有n个平均覆冰天数历史数据,m个影响因子特征值,则n个样本的m个因子组成的矩阵X为X=(xij),其中xij为第j个样本的第i个影响因子的特征值,由于m个影响因子特征值的物理量级、量纲的不同,需对预报因子特征值做以下归一化处理:

其中,ximax,ximin分别为n个样本中第i个因子的最小特征值和最大特征值。当影响因子与样本呈正相关时使用式 (2),负相关时使用式 (3),则得到了因子规格化矩阵X'=(x'ij)。
接下来需要将n个样本分为c类,将覆冰天数按轻度、中等、严重分为3类,得到模糊划分矩阵U=(uhj),uhj为样本j对类h的相对隶属度,需要满足条件
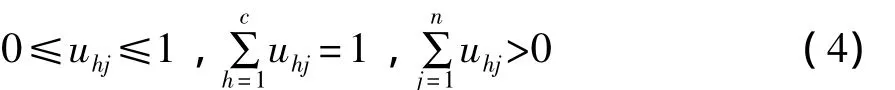
设定满足式 (4)的初始模糊划分矩阵 (uhj),根据模糊识别循环迭代模型,给定计算精度ε=10-6和权向量的初始值,即
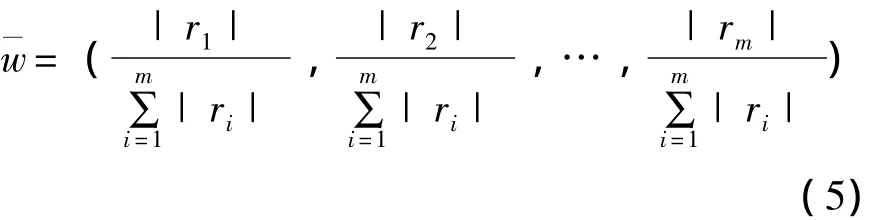
其中,r为样本与预报因子xij之间的相关系数,则可解得最优模糊识别矩阵 (u*hj)。最后根据矩阵 (u*hj)可确定n个样本3个类别的特征值向量H:

根据式 (1)计算H与n个样本间的相关系数r,r表示样本与影响因子之间的相关密切性,r绝对值越大,模糊相关程度就越高,相应地预报精度也就越高。
1.3 预报因子提取步骤
由上面的理论,可以通过以下步骤来筛选预报因子〔7〕:
(1)分别计算每个影响因子作用下的r值,为了检验其稳定性,防止假相关,可以计算多个年份的r值,记其绝对值平均为|ra|。如果r值波动很大,甚至出现正负值变化,则认为此影响因子与预报对象之间无显著相关性,可视为无效因子予以剔除。将剩余影响因子按|ra|从大到小排序,分别设为xi,i=1,2,…,m,r值分别设为ri,i=1,2,…,m。
(2)将x1暂定为有效因子,并与x2综合作用,计算得到其相关密切性r12,如果r12>r1,则视x2为有效因子,否则视为无效因子。
(3)若x2为有效因子,将x1,x2,x3综合作用,得到r123,如果r123>r12,则视x3为有效因子,否则称为无效因子;若x2为无效因子,则将x1与x3综合作用,得到r13,如果 r13>r1,则视x3为有效因子,否则视为无效因子。
重复步骤 (3),即可得到多个有效因子,表1为筛选出来的预报因子及r的绝对值平均。

表1 长期预报因子及其|ra|
2 电网覆冰的预报模型
2.1 BP神经网络模型
BP神经网络已被广泛地应用在天气气候预测中〔8〕,这里通过MATLAB中提供的神经网络函数建立电网覆冰的长期预报模型。MATLAB中对BP神经网络提供了多种可以选择的算法,这里我们选用动态自适应学习速率的梯度下降BP算法,该算法能够在较少的训练次数和较短的训练时间内达到目标精度。为了保证运算的收敛速度,训练样本量不宜过大〔8〕,取1977—2006年的湖南电网平均覆冰天数和其对应的4个前期预报因子作为模型的输入,经过多次试验发现,当隐含层节点数为5,目标精度为0.03时,模型具有较好的稳定性。运用该模型对2007—2010年的覆冰天数进行预报,结果列在表2中,其中2003—2006年的样本用于模型的校验。
2.2 逐步线性回归模型
为了比较模糊识别与神经网络相结合的预报模型与传统线性模型的优劣,建立了用途广泛的逐步线性回归模型。该模型是通过逐步引入每个变量,并每次计算变量的显著性,在最后一个变量被选择或剔除后,建立线性回归模型,其方法简单、建模方便。选取27个影响因子作为自变量,n个样本作为因变量,在MATLAB中建立逐步回归线性模型,得到了以3月亚洲纬向环流指数 (x1)、7月北半球副高脊线 (x2)、10月印度副高脊线 (x3)、10月北美副高脊线 (x4)为预报因子的线性归回模型,其表达式为:

同样将2003—2006年的样本作为模型的校验,将2007—2010对应的x1,x2,x3,x4带入式 (7),其对应Y值即预报结果也列在表2中。

表2 2003—2010湖南电网覆冰预报模型结果比较
从结果中可以看出,模糊识别方法和神经网络相结合的预报结果比逐步回归方法精度更高。但在2007年2种预报模型的预报值与实际值相差甚远,这主要是因为2007年的覆冰数据超过了历史样本均方差3倍,属于统计学中的异常值〔9〕,长期预报因子很难提供足够的预测信息对其进行准确预报,需要与中、短期预报相结合才能达到更好的预报效果。
3 结论
通过统计分析方法得到了与湖南电网覆冰相关的27个影响因子,又分别通过模糊识别和逐步回归方法从这些影响因子中筛选出了湖南电网覆冰的4个长期预报因子,并分别建立了4因子的BP神经网络预报模型和线性回归预报模型,其结果表明神经网络模型具有更好的预报效果。虽然这些长期预报模型对于2007年的严重覆冰预测得不够理想,但总体趋势预测准确,能够为电网防冻融冰计划提供指导。
〔1〕陆佳政,彭继文,张红先,等.2008年湖南电网冰灾气象成因分析〔J〕.电力建设,2009(6):29-32.
〔2〕陆佳政,蒋正龙,张红先,等.湖南电网2008年冰灾技术分析〔J〕.湖南电力,2008(3):1-9.
〔3〕徐敏亮,于会芳,冯本领.74项环流指数在水文长期预报中的应用〔J〕.黑龙江水利科技,2011(1):144.
〔4〕陈守煜.中长期水文预报综合分析理论模式与方法〔J〕.水利学报,1997(8):15-21.
〔5〕白子岩.模糊模式识别法在中长期预报中的应用〔J〕.水利水电技术,1999(2):50-51.
〔6〕李希灿,刘桂生,张波,等.水文中长期预报成因模糊综合分析预测模式〔J〕.黑龙江水专学报,1998(3):67-71.
〔7〕胡国华,宋荷花,李正最.基于人工神经网络的湘江最大洪峰流量中、长期预报〔J〕.长沙交通学院学报,2008(2):72-77.
〔8〕刘德,李晶,李永华,等.BP神经网络在长期天气过程预报中的应用试验〔J〕.气象科技,2006(3):250-253.
〔9〕施能.气象统计预报〔M〕.北京,气象出版社,2009.

