基于免疫遗传算法的含分布式电源配网规划

戴小庞，周洪，海晓涛

(1.河源源城供电公司，广东河源 517000;2.湖南省电力勘测设计院，湖南长沙 410007;3.中国电力科学研究院，北京 100192)

分布式电源 (distributed generation，DG)是指发电功率在数千瓦至50 MW的小型化、模块化、分散式、布置在配电网或用户附近的小型发电系统，具有污染少、能源利用率高、安装地点灵活等优点〔1〕。配网规划是在满足用户供电和保证网络运行约束的前提下，确定1组最优决策变量，使得投资、网损以及用户停电损失之和最小，属于离散、非线性、多目标组合优化问题〔2〕。

分布式电源大量接入配电网，其输入和输出的随机性特点使配网规划复杂性大大增加，如:单向潮流变为网格化潮流〔3〕、负荷预测更难以确定、电能质量控制更复杂、寻优变量种类和维数增加等。传统规划方法由于难以定量表达不确定因素，已难以解决含分布式电源的配网规划问题〔4〕。遗传算法虽然是一种基于多点随机搜索的启发式算法，但迭代后期由于个体多样性缺失易陷入局部最优，若通过加大交叉率和变异率来避免，则可能导致最优解搜索效率降低，从而减缓收敛速度。

为克服遗传算法在配网规划计算中的早熟收敛问题，提高遗传算法的全局收索能力，本文将免疫系统与遗传算法相结合，形成免疫遗传算法(Immune Genetic Algorithm，IGA)，可实现群体收敛性和个体多样性间的动态平衡，具有良好的全局收敛能力和收敛速度。算例验证了本文所提方法的有效性。

1 含分布式电源配网规划模型

计及分布式电源配网规划分为DG布点规划和考虑DG配网扩展规划，由于前者着重电源规划，所以本文重点对含DG配网扩展规划进行研究，即系统达到容量限制时，在满足各约束条件的前提下，以经济成本最小为目标，提出可以满足负荷增长要求的系统最佳增容方案，由电网升级、新建线路、变电所增容扩容以及在适当位置安装适当容量DG所组成的最佳方案〔5〕。

(1)目标函数

考虑到配电网设备使用寿命与分布式电源有所不同，本文采用等年值法将投资费用折算为年费用，目标函数为:

式中 CL为折算到每年的线路建设费用和运行费用;CDG为分布式电源的年发电费用 (包括建设费用、运行费用、燃料费用等);Cen为从常规电源购电的年费用。(2)等式约束条件节点功率平衡约束:

式中 Sij和Sji分别为支路ij的正、反向潮流;M，N分别为系统节点总数和负荷节点总数;Zij和ΔUij分别为支路ij的阻抗和两端电压降;SDG，j为节点j处DG的装机容量;Pj为节点j的负荷需求。

(3)不等式约束条件

电流约束:Iij≤Iijmax

电压约束:Uimin≤Ui≤Uimax

分布式电源容量约束:

为使分布式电源接入后的配网潮流可控，限制分布式电源的最大接入总容量为系统新增负荷总量的20%。

式中 Iij和Iijmax分别为支路ij上电流及最大电流限值;Ui和Uimin，Uimax分别为节点i电压及节点电压上、下限;SDGmax为新增负荷总量的20%。

(4)辐射状运行约束

M=L+1

式中L为新建线路数及原有线路数总和。

2 基于免疫遗传算法的含分布式电源配网规划

免疫遗传算法是基于生物免疫机制提出的一种改进的遗传算法，将求解问题的目标函数即年费用最小对应为入侵生命体的抗原，而含DG配网优化规划的解对应为免疫系统产生的抗体。

(1)抗体编码

采用变长度的整数编码，编码长度与DG接入比例以及每个DG容量相关。DG布置方案由变量C={c1，c2，…，cn}确定，ci为零表示节点i不安装DG;ci为整数K则表示节点i规划安装DG且其容量为K×0.1 MVA。

(2)产生分布式电源位置和容量的初始抗体

DG位置和容量方案的随机产生会出现许多不可行解，为提高免疫遗传算法搜索的速度、效率和最终收敛到全局最优解，文中产生DG位置和容量初始抗体的步骤如下:

①计算配网新增负荷总量，DG最大接入总量为新增负荷总量的20%;

②对随机生成初始抗体群进行校验，若所有抗体对应的DG容量小于相应位置的负荷量，且总接入容量小于规定值，则该抗体群作为DG位置和容量的初始解;否则重新生成抗体，替换不符合要求的抗体。

(3)产生配电网扩展规划的初始抗体

配电网扩展规划主要是待建线路的选择，既要保证连通性又要具有辐射性。考虑到随机产生的初始抗体群存在大量不可行解，文中采用根节点融合法〔5〕产生初始抗体群，其中修建线路用1表示，不建线路用0表示。

(4)计算抗体亲和度和抗体浓度

依据目标函数的值决定抗原与抗体的亲和度，依据解的相似程度决定抗体之间的亲和度，利用这2种亲和度对抗体进行评价和选择。

抗体i浓度=与抗体i相似度大于λ的抗体数和/抗体个数;λ为相似度常数，本文取0.95。

(5)抗体的抑制和促进

保留抗体群中浓度最大的抗体，为维持种群的多样性，防止抗体群向单一化发展，对浓度较高的抗体进行抑制淘汰，随机产生新的个体代替被淘汰的个体。通过计算抗体的期望值来决定抗体的生存率，期望值等于抗体的亲和度比上抗体浓度，若期望值高则被选择的概率就大，使得与抗原亲和度高而浓度低的抗体得到促进;否则，抗体得到抑制。

(6)交叉和变异

在2个父代抗体上随机选择一个交叉点，按交叉概率Pc仅交换该点对应基因。若交叉后出现环路，则分别断开其支路，寻找抗体对抗原适应度最大的支路;若出现孤立节点集，分别选择与孤立节点相连的支路，寻找抗体对抗原适应度最大的支路。

将抗体中随机确定的基因按变异概率Pm进行取反操作，满足连通性和辐射性作为子个体，否则采用与交叉相同的方法进行可行性处理。

基于免疫遗传算法的含DG配网规划流程如图1所示。

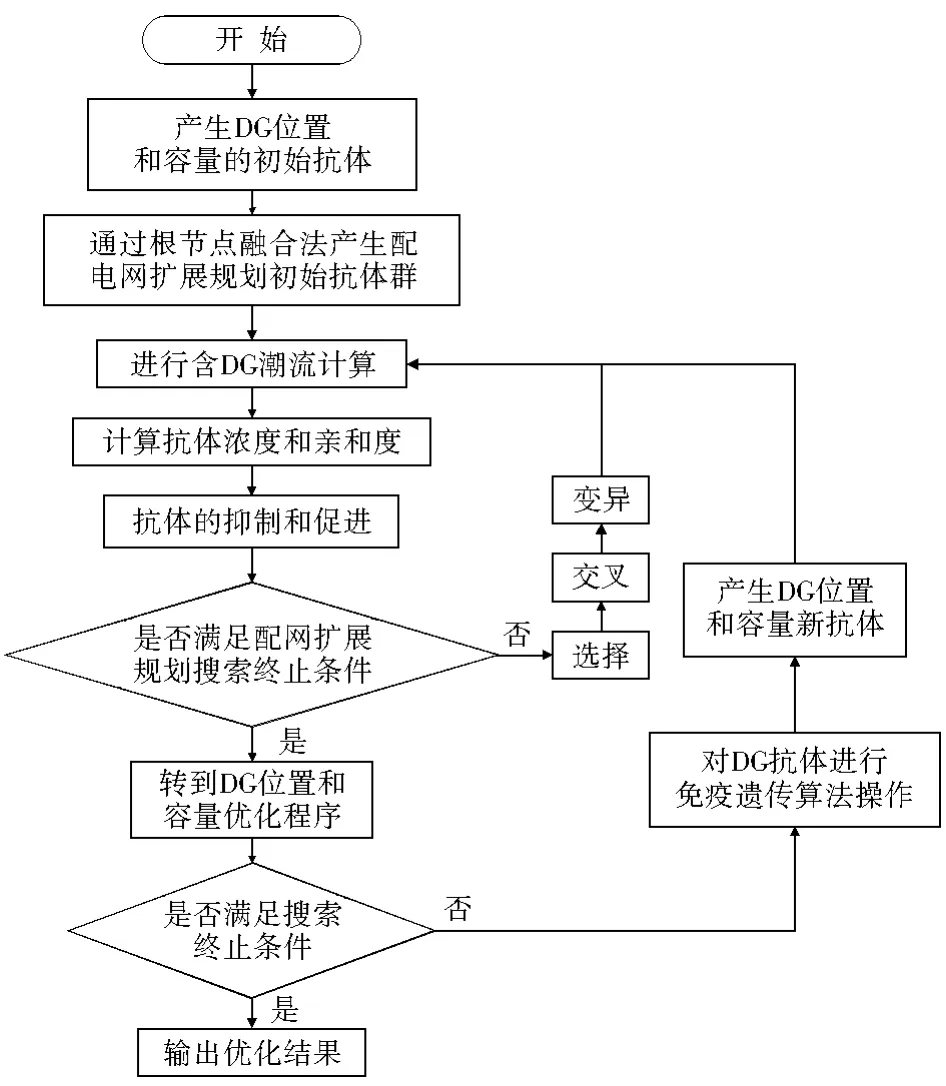
图1 基于免疫遗传算法的含DG配网规划流程图

3 算例与分析

分别运用简单遗传算法和文中提出的免疫遗传算法对图2所示的配电网进行DG定位、定容和网络优化规划。实线为已有线路，虚线为待选线路，节点负荷数据及其他系统参数见文献〔6〕。节点1为配电站，其余为负荷节点，节点4—10为新增节点，节点2—10允许接入DG。

图2 配电网初始结构

由文献〔6〕节点负荷数据可知，新增有功负荷为4.8 MW，假设单个DG功率因数为0.9，则DG在电网最大接入容量为1.07 MVA。文中抗体规模取50，最大进化代数为100，Pc为0.9，Pm为0.02。

采用简单遗传算法得到DG安装位置分别为节点5，9，10，容量均为0.3 MVA，安装DG后配网扩展优化规划方案如图3所示。运用免疫遗传算法计算得到DG安装位置分别为节点3，9和10，容量分别为0.4 MVA，0.3 MVA和0.2 MVA，安装DG后配网扩展优化规划方案如图4所示。由于DG对线路潮流的影响，可以看出DG主要位于辐射线路的中末端。无DG配网扩展优化规划方案如图5所示。3种规划方案的费用比较如表1所示。

图3 含DG配网优化规划 (简单遗传算法)

图4 含DG配网优化规划 (免疫遗传算法)

图5 不含DG配网优化规划结果

由表1可看出:

(1)DG接入对线路负载能力和潮流的影响使得线路投资、运行费用以及网损费用均低于无DG接入的配网规划，其中网损费用减小最为突出;

表1 不同规划方案费用 万元

(2)采用免疫遗传算法优化的网络的线路费用、网损费用及总费用比遗传算法优化后网络的相关费用均有所减少，其中总费用减少5.366万元;

(3)因目前DG发电成本仍较高，含DG配网规划的经济优势相对不明显。但是DG接入系统所带来的巨大的社会效应，以及随着技术发展带来DG成本的降低，使得在配网中引入DG具有重要的意义。

4 结论

文中以年费用最小为目标函数建立了含DG配网规划数学模型，并提出采用免疫遗传算法解决该复杂问题。通过算例分析，文中提出的免疫遗传算法较简单遗传算法更适合于求解含DG的配网规划问题，得到的含DG规划方案较无DG规划方案具有很大的经济和社会效益。

〔1〕张建华，黄伟.微电网运行控制与保护技〔M〕.北京:中国电力出版社，2010:1-26.

〔2〕方兴，郭志忠.配电网规划研究述评〔J〕.电力自动化设备，2003，23(5):71-74.

〔3〕苏玲，张建华，王利，等.微电网相关问题及技术研究〔J〕．电力系统保护与控制，2010，38(19):235-239.

〔4〕王成山，陈恺，谢莹华，等.配电网扩展规划中分布式电源的选址和定容〔J〕.电力系统自动化，2006，30(3):38-43.

〔5〕王凌.智能优化算法及其应用〔M〕.北京:清华大学出版社，2001:25-38.

〔6〕杨期余.配电网络 (第1版)〔M〕.北京:中国电力出版社，1998:42-57.