基于偏微分方程解析求解的图像矢量化方法

张靖磊，余正生，樊志华，朱婧

(1.杭州电子科技大学图形图像研究所，浙江杭州310018;2.杭州电子科技大学机械工程学院，浙江 杭州310018)

0 引言

在科学工程领域中，图像矢量化技术有着非常广泛的应用，图像矢量化是将光栅图像转换为矢量图形。矢量图形体积小，可扩展，易于编辑，最大的优点在于无论放大、缩小或旋转等不会失真。不同于光栅图形，矢量图用点、直线或者多边形等基于数学方程的几何图元来表示图像，便于图像的处理［1］。基于矢量图的这些优点，在大量领域中都用到了矢量图形。由于图像复杂性和多样性，图像矢量化的方法也有所不同，比较有代表性有基于细化的矢量化方法［2］，抽取图像轮廓线并进行矢量化的方法［3］，用给定的正方形网格分割图像［4］。偏微分方程(Partial Differential Equation，PDE)曲面［5］是一种新出现的强有力的曲面造型工具。PDE方法将曲面看作椭圆型偏微分方程在边界条件下的解，由于PDE方法只需少量边界条件即可表示复杂的三维曲面，所需存储量少因而高效。近年来国外学者研究了采用椭圆型偏微分方程作为曲面模型，将从未知曲面提取出的轮廓线作为边界条件，通过PDE方法拟合曲面的基本原理和应用［6］。本文利用偏微分方法构造曲面的原理，提出了利用偏微分解析求解进行图像矢量化方法，提取图像的轮廓线作为边界条件，通过求解析解法进行拟合，能有效的将处理图形的方法来处理图像。

1 PDE方法图像矢量化

这一部分介绍利用偏微分方程构造曲面的原理以及如何使用解析解法进行图像矢量化。

1.1 PDE法构造曲面的原理

在应用中，通常将曲面表示为含有参数的形式:X(u，v)。设 X(u，v)=(x(u，v)，y(u，v)，z(u，v))表示曲面上的点，参数u，v看作是在从平面区域Ω到物理空间上的映射，记为:Ω→R3。PDE曲面是一个参数曲面 X=X(u，v)，通常采用椭圆偏微分方程［7］。设 Ω ={0≤u≤1，0≤v≤2}，给定类双调和方程:

将取待生成的偏微分方程曲面的4条轮廓线作为4个边界条件，给定方程1的4个傅里叶级数表示的周边边界条件:

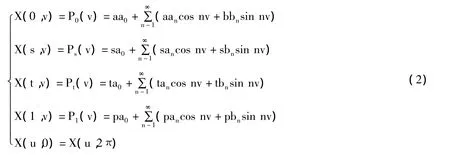
式中，P0(v)，P1(v)分别定义了曲面在u=0，1上的边界曲线;Ps(v)，Pt(v)分别定义了曲面在内部u=s，t上的边界曲线。X(u，0)=X(u，2)表示边界条件是周期的，即曲线为闭曲线。通过分离变量法得到式1、2的解:

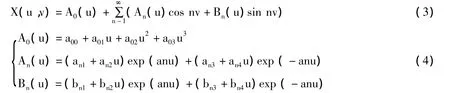
由式2、4得知:

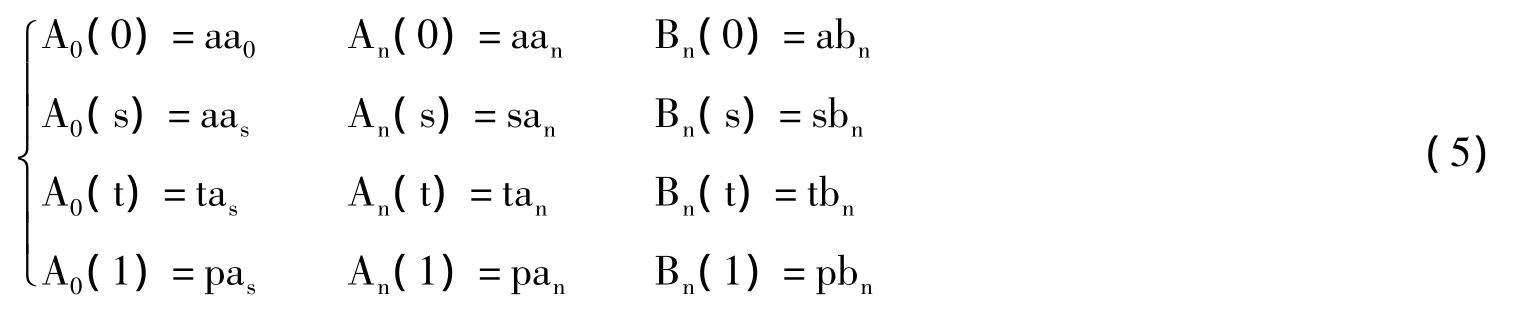
方程组中，未知数和方程个数都是为 4 个，可以求出 aa0，sa0，ta0，pa0，aan，san，tan，pan，abn，sbn，tbn，pbn。若假设 s=0.333 33，t=0.666 67 给定边界条件:

由式6可知傅里叶级数的最高项cosv和sinv，最高项决定了n的取值上限，即n最大为1。则式3演化为:

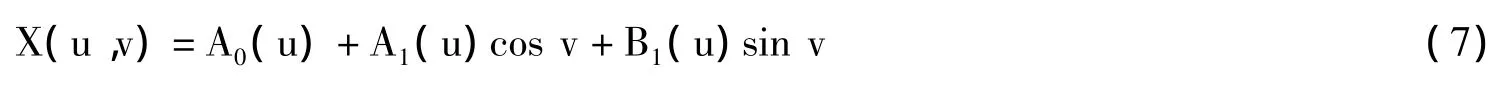
将 u=0，s，t，1 代入 A0(u)，An(u)，Bn(u)中，解得:a00=0.000 00，a00=3.000 13，a00= －0.000 40，a00=0.000 27。同理可解 a10，a11，a12，a13，b10，b11，b12，b13。则曲面为:边界曲线如图1所示，生成的PDE曲面如图2所示:

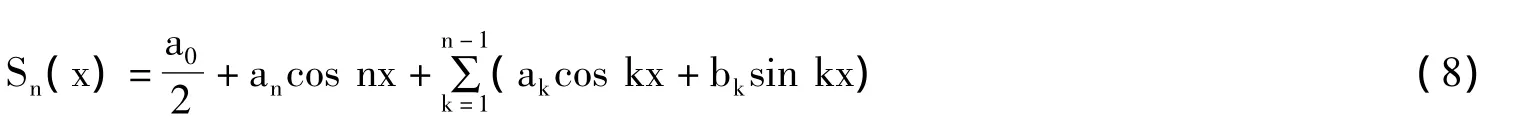
图1 由(6)生成的四条边界曲线

图2 由图1生成的PDE曲面

1.2 基于PDE法的图像矢量化

通过偏微分方程实现图像矢量化，一张图片有很多个象素点，每一个都有一个特定的坐标、象素值，记为P(x，y，r，g，b)，为了确定边界条件，由式2可知边界条件需拟合成傅里叶形式的曲线，对这些散乱点按特定的要求，求其离散最小二乘逼近［8］来拟合出一条傅里叶级数曲线。如图3所示:

图3 一个鸡蛋的例子

例如图3(a)的一点为 P(139，31，0.949，0.922，0.859)，为了达到一定的拟合效果，取n=20，例如图3中第一条被拟合成的曲线系数如下所示(系数形式(ak，bk)):(303.000，0.000)(－ 10.512，0.636)(0.000，0.000)(－1.145，0.210)(0.000，－0.000)(－0.396，0.123)(0.000，0.000)(－0.190，0.085)(－0.000，－0.000)(－0.105，0.064)(－0.000，－0.000)(－0.063，0.049)(－0.000，0.000)(－0.038，0.038)(0.000，－ 0.000)(－ 0.024，0.030)(0.000，－0.000)(－0.014，0.023)(－0.000，0.000)(－0.008，0.017)。依据这些系数，得到边界条件。依据边界条件，可知:X(0，v)=P0(v)，X(s，v)=Ps(v)，X(t，v)=Pt(v)，X(1，v)=P1(v)，X(u，0)=X(u，2)。

每4条边界条件生成一个PDE曲面，相邻2个曲面片之间共用1条边界曲线，如图4所示:

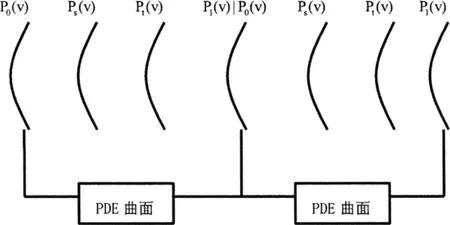
图4 7条边界曲线构成2个PDE曲面片

若曲面由n个曲面片组成，则边界曲线共有3n+1条。因此每一个图像块等同于是一张PDE曲∞面，图像块满足 X(u，v)=A0(u)+n∑－1(An(u)cos nv+Bn(u)sin nv)，图 3(b)显示了(a)图经过图像矢量化后的图像。

2 基于PDE方法图像矢量化的例子

依据前面的方法，这一部分展示了两个例子。如图5所示:

图5 一个红椒的例子

图5 (a)是扫描出来的图像，图5(b)显示了图5(a)经过图像矢量化后的图片。对原图的象素点进行最小二乘逼近，拟合成207条傅里叶曲线作为边界条件。

依据每4条边界条件生成一个PDE曲面，相邻2个曲面片之间共用1条边界曲线，则共有130个曲面片，每个曲面片通过4条边界曲线唯一的确定。

3 结束语

根据椭圆偏微分方程的表示，本文首先介绍了PDE方法构造曲面的基本原理;然后对提取出来的图像的离散点进行最小二乘拟合，以图像的轮廓线作为边界条件，划分图像块，运用PDE解析解方法高效的重构一张图像;PDE方法简单易行、速度快，并由于边界条件生成的图像块保留了原始图像的基本特征，能高效的重构图像。本文所提出的方法对于图像不是很复杂的情况下还是十分高效和方便的。

［1］ 彭容杰.图像矢量化方法研究与英语［D］.武汉:华中科技大学，2006.

［2］ Pavilidis T.An asynchronous thinning algorithm［J］.Computer graphics and Image Processing，1982，20(2):133 －157.

［3］ Hori O，Tanigawa S.Raster－to－Vector Conversion by Line Fitting Based on Contours and Skeletons［C］.Tsukuba Science City:Document Analysis and Recognition，1993:353－358.

［4］ Vaxiviere P，Tombre K.CAD Conversion of Mechanical Drawings［J］.IEEE Computer，1992，25(7):46 －54.

［5］ Bloor M I G，Wilson M J.Generating blend surfaces using partial differential equations［J］.Computer－ Aided Design，1989，21(3):165 －171.

［6］ Ugail H，Kirmani S.Shape Reconstruction using Partial Differential Equations［J］.WSEAS Transactions on Computers，2006，10(5):2 156 －2 161.

［7］ 朱心雄.自由曲线曲面造型技术［M］.北京:科学出版社，2008:250－271.

［8］ Richard L Burden，Douglas J Faires.数值分析［M］.北京:高等教育出版社，2005:420－445.