高阶WENO格式数值粘性对模拟R-T不稳定性的影响

王革，谢昌坦，张斌

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001;2.北京航空航天大学宇航学院，北京100083)

受扰动的轻重流体的交界面，当受到方向由重流体指向轻流体的重力或惯性力作用时，扰动将发展，界面将失稳，2种物质将发生湍流混合，这种不稳定现象称为Rayleigh-Taylor(R-T)不稳定性.当相互接触的2层流体间存在切向速度差时，界面也会扰动发展，这种不稳定现象称为 Kelvin-Helmholtz(K-H)不稳定性.一般在R-T不稳定性发展的后期，流体界面处会产生强剪切流，K-H不稳定性被激发并导致流体的小尺度混合.因此，R-T不稳定性常常伴随着K-H不稳定性，而后者的出现加重了前者后期的非线性发展，加剧了界面附近流体的混合程度.上述2种不稳定性在天体物理、激光聚变、高速碰撞和加速等高技术领域中都是客观存在的，甚至对水力机械以及各种发动机也都是非常重要的［1］.

由于R-T不稳定性自身的复杂性，一般只有采用高阶精度格式才能获得较好的模拟效果.1987年，Harten等提出了一种完全考虑TVD性质，通过节点模板的单调选择、扩展来达到高分辨率的数值方法——ENO 格式［2］，而后 Osher、Shu 等避开节点模板选择，利用加权思想构造了WENO格式［3-4］.大量的理论研究和实验表明，ENO和WENO格式特别适合用于求解既包含激波、间断又包含光滑区域的复杂流场.

任何数值格式都具有数值粘性，而且数值粘性的大小有时会对数值解产生很大影响.格式的精度越高，计算网格越密，则数值粘性越小.然而数值粘性的定量求解是一项极其繁杂的工作，这点对于高分辨率格式尤为突出.为此本文主要通过一个经典的二维R-T不稳定性算例定性研究了高阶WENO格式的数值粘性，分别应用3、5、7、9阶精度WENO格式求解二维无量纲Euler和Navier-Stokes方程获得了不同网格尺度下无粘和有粘时的数值解.通过研究R-T不稳定性后期激发出的K-H不稳定性的强弱，分析了数值粘性和物理粘性对数值流场细微结构的影响趋势.

1 控制方程及其数值解法

含有重力源项(假设重力方向竖直向上，重力加速度取)的二维无量纲Navier-Stokes方程为

式中:ρ、p分别表示流体的密度和压力，u、v分别表示流体沿 x、y方向的速度分量，总能)，γ为比热比，Pr为普朗特数，Re为雷诺数.当S(U)=0即Re→∞时，式(1)便退化为含有重力源项的Eluer方程.

采用文献［5］介绍的时间分裂法求解式(1)，即将式(1)分解为Euler方程和源项2部分单独求解，如下:

式(2)的空间项分别采用基于特征分解法的3、5、7、9 阶有限差分型 WENO-LF 格式求解［6-7］，时间项采用三阶TVD-Runge-Kutta法求解［3］.为保证与式(2)的精度一致，式(3)的空间项分别采用2、4、6、8 阶中心差分格式，时间项采用三阶Runge-Kutta法求解.

2 数值算例及结果分析

本算例的计算区域为［0，0.25］×［0，1.0］，计算网格为方形网格，其宽度用h表示.初始时刻界面位于y=0.5处，重气体位于界面以下，参数为ρ=2.0，u=0.0，p=2y+1，v=-0.025c cos(8πx);轻气体位于界面以上，参数为 ρ=1.0，u=0.01，p=y+1.5，v=-0.025c cos(8πx)，c 为音速，c=，γ =1.666 7，Pr=0.7.左右边界设为反射边界条件，上下边界设为无反射边界条件，上边界参数为 ρ=1.0，u=0，p=2.5，v=0，下边界参数为 ρ=2.0，u=0，p=1，v=0.计算至时刻 t=1.95.

2.1 无粘情况

无粘情况下的数值流场是通过求解Euler方程得到的.图1为不同精度WENO格式和不同网格数量条件下区域［0，0.25］×［0.2，0.9］的 15 条密度等值线分布图.为简便，引入符号WENO-N-X，其中，N代表WENO格式的精度，N=3、5、7、9;X 代表计算网格的宽度 h，X=C(h=1/400)、M(h=1/800)、F(h=1/1 600).

从图1可以看出，采用Euler方程模拟R-T不稳定性，数值格式的精度和网格的数量对其数值解有很大影响.WENO-3-C、WENO-3-m和 WENO-5-C的数值结果基本相同.在重力作用下，下层重流体以尖钉的形式侵入上层轻流体，而上层轻流体以气泡的形式侵入下层重流体，两层流体交界面形成了清晰的蘑菇状结构，这种结构也是R-T不稳定性发展到后期的典型结构.由于此时数值格式的数值粘性较大，K-H不稳定性较弱，流体的交界面比较平滑.比较WENO-3-F、WENO-5-M，WENO-5-F，WENO-7-C，WENO-7-M，WENO-9-C，WENO-9-M可知，随着格式精度的提高和网格数量的增加，数值格式的数值粘性减弱，K-H不稳定性增强，蘑菇的伞状结构在轻流体的作用下翻转，并在K-H不稳定性的作用下断裂、碎化，轻重流体混合加剧，导致伞状结构内部的流场极其复杂，两层流体的交界面变得模糊.蘑菇的杆状结构处也出现了涡状结构，但因涡的形状比较大、数量少且排列有序，流体交界面仍然清晰可辨.高精度密网格情况下，数值流场的对称性结构被破坏，如WENO-7-F和WENO-9-F所示，这完全是由Euler方程本身造成的，此时所得的数值解是非物理的［8-9］.

图1 无粘时的密度等值线分布Fig.1 The contour lines for density for non-physical viscosity

所以，当采用Euler方程模拟R-T不稳定性时，由K-H不稳定性导致的物质界面处复杂结构的细节强烈依赖于所采用数值格式的数值粘性，网格细化所得的数值解一般不具有强收敛性，而且当网格过度细密时，数值流场的复杂结构往往是非物理的.正确计算R-T不稳定性的方法应当采用带有真实物理粘性的 Navier-Stokes方程［8，10］，如3.2 节所示，当数值格式的数值粘性远远小于流体的物理粘性时，所得的数值解一般是可信的.

2.2 有粘情况

图2、3分别为雷诺数Re=30 000，60 000时的15条密度等值线分布图.为了能更好的了解R-T不稳定性的数值解随网格数量的变化情况，取图2和图3中y=0.6处即流场结构最复杂地方的密度沿x方向的分布为研究对象，如图4、5所示，相应的L1误差［10］列于表1、2.

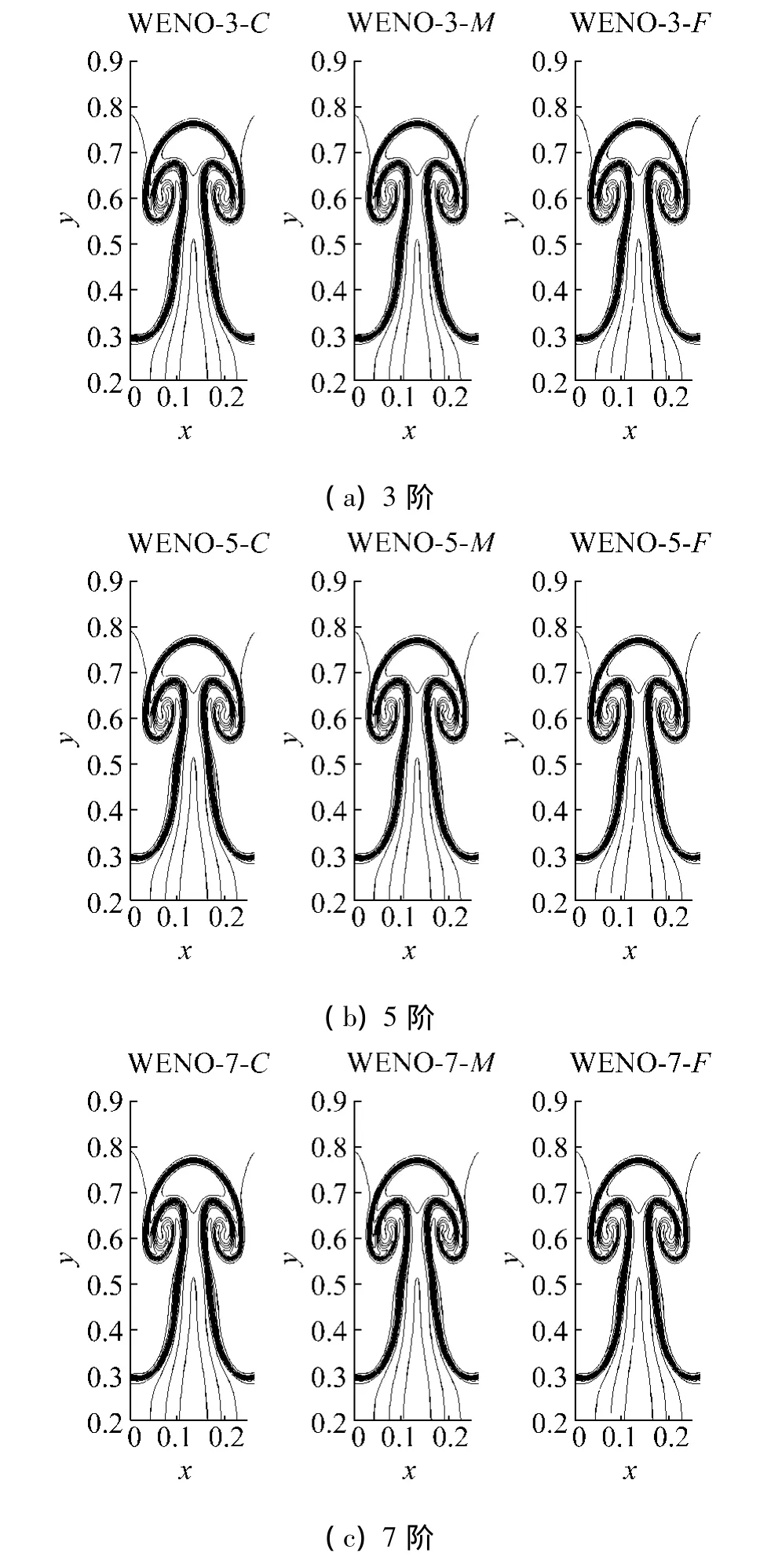
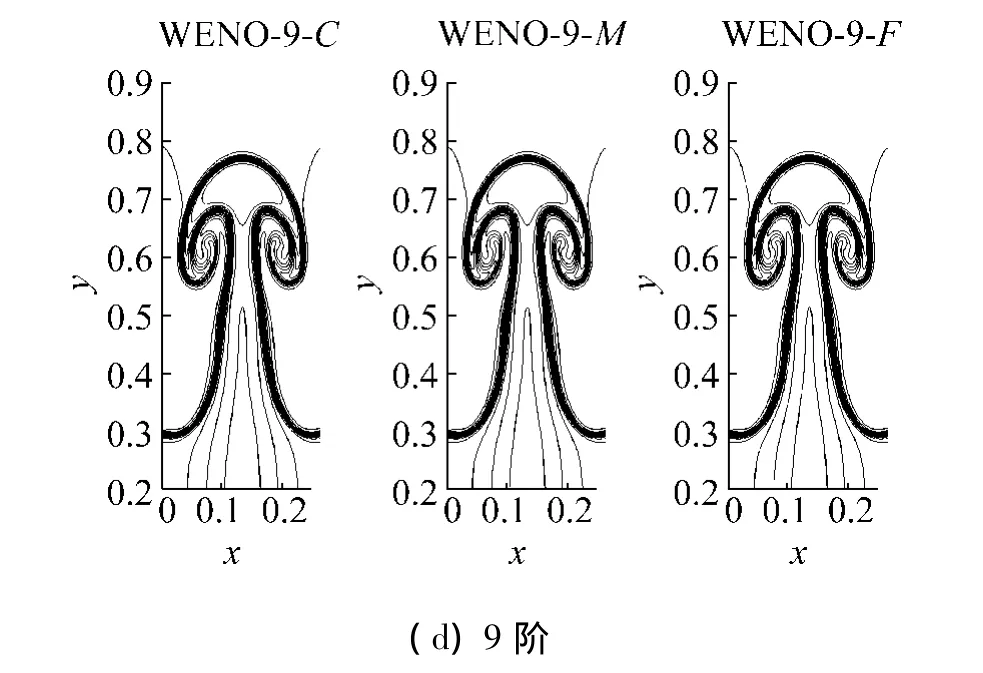
图2 Re=30 000时密度等值线分布Fig.2 The contour lines for density with Re=30 000

可以看出，采用Navier-Stokes方程模拟R-T不稳定性，随着网格数量的增加，WENO格式的数值粘性逐步减小，流体的物理粘性逐步占优，L1误差减小.若规定L1≤1.2×10-3时数值解收敛，那么当Re=30 000时，WENO-5-M、WENO-7-M、WENO-9-m及 WENO-N-F的数值流场已基本稳定;Re=60 000时，WENO-7-M、WENO-9-m和 WENO-5-F、WENO-7-F、WENO-9-F的数值解已基本收敛，这说明此时数值格式的数值粘性已经远远小于流体的物理粘性了.同一雷诺数条件下，不同精度WENO格式所获得的稳定流场的结构基本相同，且格式的精度越高，获得稳定解所需的网格越少.同一精度条件下，雷诺数越高，流体的物理粘性越小，则掩盖数值粘性的影响所需的网格也就越多，稳定流场的结构越复杂.

图3 Re=60 000时密度等值线分布Fig.3 The contour lines for density with Re=60 000

图4 Re=30 000时y=0.6处密度沿x方向的分布Fig.4 Distribution of density along x at y=0.6 with Re=30 000

表1 Re=30 000时WENO-N-X的L1误差(×102)Table 1 The L1 error of WENO-N-X when Re=30 000

图5 Re=60 000时y=0.6处的密度沿x方向的分布Fig.5 Distribution of density along x at y=0.6 when R e=60 000

表2 R e=60 000时WENO-N-X的L1误差(×102)Table 2 The L1 error of WENO-N-X when Re=60 000

图6给出了Re=140 000时WENO-9的密度在不同网格数量条件下的分布图，y=0.6处的密度沿x方向的分布如图7所示.可以看出，图6中的前3幅图的密度分布随网格的加密变化较大，如图7(a)所示.这是因为在雷诺数很高的情况下，流体物理粘性很小，网格较粗时的数值粘性占绝对优势，初步加密网格后其值迅速减小但仍远大于物理粘性.随着网格的继续加密，物理粘性的影响开始体现出来并且逐步占优，流场结构随着网格数量的加密变化缓慢，当网格加密到一定程度后，数值粘性便远小于物理粘性了，流场结构达到稳定状态，如图7(b)所示.稳定流场的流体交界面比较平滑，蘑菇的伞状结构内部形成了2个较大且清晰的涡状结构，杆状结构的下部也形成了2个较小的涡状结构.

图6 Re=140 000时WENO-9的密度等值线分布Fig.6 Distribution of numerical density for WENO-9 with Re=140 000

图7 Re=140 000时y=0.6处的密度沿x方向的分布Fig.7 Distribution of density along x at y=0.6 with Re=140 000

3 结论

本文通过利用高阶WENO格式求解无粘Euler和Navier-Stokes方程模拟了二维可压缩流体中的R-T不稳定性问题.数值结果表明，R-T不稳定性的复杂流场结构的细节取决于其后期激发出的K-H不稳定性的强弱.无粘情况下，K-H不稳定性的强弱取决于所采用的数值格式的数值粘性，也就是格式的精度和网格的数量;有粘情况下，随着精度的提高和网格的细化，当数值粘性远小于物理粘性时，流场的细微结构唯一取决于流体的物理粘性，所得到的数值解是可信的.

［1］王继海.二维非定常流和激波［M］.北京:科学出版社，1994:348-471.WANG Jihai.Two dimensional unsteady flows and shock waves［M］.Beijing:Science Publishing Press，1994:348-471.

［2］HARTEN A，ENGQUIST B，OSHER S，et al.Uniformly high order essentially non-oscillatory schemes［J］.JComput Phys，1987，71:231-303.

［3］JIANG G S，SHU CW.Efficient implementation of weighted ENO schemes［J］.J Comput Phys，1996，126:202-228.

［4］LIU X D，OSHER S，CHAN T.Weighted essentially nonoscillatory schemes［J］.JComput Phys，1994，115:200-232.

［5］TORO E F.Riemann solvers and numericalmethods for fluid dynamics［M］.3rd Ed.Berlin:Springer，2009:531-542.

［6］KAMANISN A，DOUGALIS V A，EKATERINARIS JA.Effective computationalmethods for wave propagation［M］.NewYork:Chapman＆ Hall/CRC，2008:533-540.

［7］BALSARA D S，SHU CW.Monotonicity preserving weighted essentially nonoscillatory schemes with increasingly high order of accuracy［J］.J Comput Phys，2000，160:405-452.

［8］SHI J，ZHANG Y T，SHU CW.Resolution of high order WENO schemes for complicated flowstructures［J］.JComput Phys，2003，186:690-696.

［9］SAMTANEY R，PULLIN D I.On initial-value and self-similar solutions of the compressible Euler equations［J］.Physics of Fluids，1996，8:2650-2655.

［10］ZHANG Y T，SHIJ，SHU CW，etal.Numerical viscosity and resolution of high order weighted essentially non-oscillatory schemes for compressible flowswith high Reynolds numbers［J］.Physical ReviewE，2003，68:046709.