水下航行体超空泡外形控制的数值研究
胡晓,郜冶,熊永亮
(哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001)
航行体在高速入水和水下高速运动过程中,会产生空泡(或超空泡),空泡的外形和尺寸会对航行体的水动力特性产生重大影响,从而影响实际的水弹道以及对航行体的控制[1-2].
要维持理想的流动体制,对超空泡外形的控制就非常必要,目前国内公开的文献中主要是通过改变空化器线性和外形参数来控制空泡形态[3-5],Savchenko Yu.N对锥形空化器和Σ形空化器开展了研究,给出了它们的阻力特性与形状参数和空化数的函数关系式,同时还对Σ形空化器的稳定性进行了深入的研究分析[6];或者通过采用非零攻角的空化器来实现非对称超空泡流动模式,从而达到控制水下高速航行体运动姿态和受力的目的,Waid[7]和Semenneko[8]对带攻角的空化器形成的空泡形态进行了研究,黄海龙等[9]通过数值模拟的方法详细分析了不同攻角的圆盘空化器生成自然超空泡的形态特征及升阻力特性.
当航行体运动速度增加并接近蒸汽空泡状态时,可以通过改变空化器阻力系数cx0来控制超空泡参数,随着空化器阻力系数的变化,超空泡尺寸也会相应改变.
本文对不同中心锥角的变阻力空化器在空泡外形的控制能力进行了数值研究,比较了不同中心锥角空化器的阻力系数和空泡尺寸响应速度;并提出了一种新的空泡控制方案,数值模拟结果也证明了该方案在阻力控制方面的灵敏性和可操作性.
1 控制方程与数值模型
1.1 控制方程
利用 FLUENT6.2中的 Mixture多相流模型[10],对混合相的连续性方程和动量方程进行求解.
混合相连续性方程:

式中:xi为笛卡尔坐标向量,ρm为混合介质密度:

式中:αk、ρk分别表示第k相的体积分数和密度,ui
为混合物的质量平均速度:

式中:uk为第k相的速度矢量.
混合相动量方程:

式中:p为压力,μt为湍流粘性系数,μm为混合粘性系数,其表达式如下:
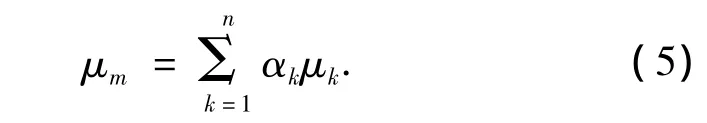
式中:μk为第k相的粘度.
湍流模型采用标准k-ε两方程模型,近壁区域的流动采用标准壁面函数法处理.
1.2 自然空化模型
FLUENT6.2中的自然空化模型[11]模拟的空泡流包括水和水蒸汽介质,空泡流建模采用混合均质流理论,整个混合物允许对流,蒸汽相传输方程如下:

式中:f为蒸汽相质量分数,Re和Rc是蒸汽产生和溃灭项:

式中:下标l和v分别表示液相和汽相,σ为液体的表面张力,Ce和Cc为经验常数,其值分别为0.02和 0.01.
1.3 动网格技术
采用动态分层法对变形区域网格进行更新,与动边界相邻的网格层(图1中的层j)依据其网格高度h被切割或与下一网格层(图1中的层i)合并,具体法则如下:
hmin>(1+αs)hideal,j层网格被分割;hmin<αchideal,j层网格被合并(溃灭).
其中,hmin为网格层j的最小网格高度,hideal为理想网格高度,αs、αc分别为网格层分割和溃灭因子.
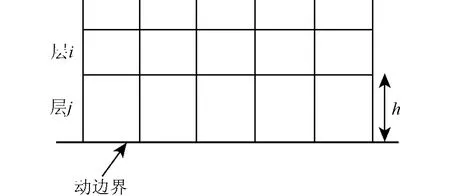
图1 动态分层法Fig.1 Dynamic layering method
2 数值计算
2.1 传统变阻力空化器
图2是文献[12-13]中提到的变阻力空化器.空化器由带尖锐前缘的外腔体1,以及安装于腔体内部,与1有着相同直径Dn的中心锥形元件2组成.通过改变外体1和中心元件2的相对位置,可以使空化器在不改变直径的情况下阻力发生变化.

图2 传统变阻力空化器示意图Fig.2 Scheme of the traditional variab le-drag cavitator
试验[6]研究表明,空化器阻力系数cx和工作行程x的变化幅度均随中心元件锥角2β的减小而增大,可以看出,中心锥角2β=60°时,在工作行程内可得到阻力系数几乎3倍的变化.
由于以上试验是基于稳态过程进行的,并不能反映超空泡外形随阻力变化的瞬态响应,本文展开了基于动网格技术的空泡流瞬态数值计算.图3为中心元件锥角2β=90°时变阻力空化器附近的网格划分.
计算中设置入口速度为30 m/s,空化数为0.174.初始时刻,中心元件最左端与外体尖缘部分位于同一竖直平面(x=h),首先进行自然空泡流的稳态计算,并以此作为动态计算的初始流场,之后中心元件在12 s内以uc=0.1m/s的速度往前移动,其中空泡面定义为蒸汽相体积分数为0.5的等值面.

图3 90°锥角变阻力空化器附近网格Fig.3 Grid around the variable-drag cavitator,2β =90°
2.2 变阻力空化器瞬态空泡流模拟结果分析
2.2.1 不同中心锥角空化器的空泡流计算结果
图4给出了2β=60°、90°的变阻力空化器在不同工作行程x处的空泡外形.可以看出:1)虽然空化器一直向前运动,但在中心元件完全露出来之前(0≤x≤h),空泡长度几乎没有变化;2)随着中心元件的继续运动,其尖缘部分开始空化,空泡长度也逐渐减小,达到稳定后不再变化;3)中心锥角越大,稳定状态所对应的工作行程越大:2β=90°时,空泡长度在x=-0.8Dn之后便不再变化,而且由于空化器阻力在x=-0.3Dn处的突然降低,在原来较大的空泡与新生成的较小空泡之间形成了明显的阶梯式边界(见图4(b)),这与文献[6]中观察到的空泡形态相符.


图4 不同工作行程处的空泡外形Fig.4 Cavity shapes at different working stokes
图5给出了60°、90°和120°中心锥角空化器的阻力系数计算结果(其中阻力系数Cd=F/0.5ρv2S,F为阻力,S为空化器的最大横截面积).图5(a)为90°中心锥角空化器的阻力系数计算值与试验数据的对比,由曲线可以看出,模拟值与试验值变化趋势大体一致,与模拟结果相比,稳态试验中的阻力随工作行程的增加,其增长速度更为缓慢.由图5(b)可以看出,中心元件的运动使空化器的阻力系数发生了明显变化,其变化的幅度随中心锥角的减小而增大,其中60°锥角的变阻力空化器在工作行程内可得到阻力系数约2.4倍的变化,这与试验数据是相吻合的;阻力系数在初始时刻最大,其最大值与圆盘空化器的阻力系数相接近;随着中心锥角的减小,空化器对应的阻力系数下限值也有所降低.


图5 阻力系数随工作行程的变化曲线Fig.5 Curves of drag coefficients of the cavitator on working stokes
图6为无量纲空泡尺寸的变化曲线,由图6知,空泡长度Lc和最大直径Dc的变化趋势基本一致:即在x=0.0Dn处空泡尺寸由最大值开始减小,x=-0.80Dn处,空泡长度及最大直径降至最低,之后不再变化;Lc、Dc的变化幅度随锥角的减小而增大:2β=60°时,工作行程内可得到空泡长度1.15倍和最大直径1.29倍的变化.不同中心锥角的变阻力空化器可获得的最大空泡尺寸与中心元件形状无关,当工作行程值x接近中心元件高度h时(见图2(a)),空泡尺寸达到最大.
结合阻力系数和空泡尺寸的变化曲线可以看出,两者变化并不同步,空泡长度及最大直径变化要滞后于阻力的变化,初始时刻(x=h),阻力系数和空泡尺寸取得最大值,之后随着工作行程值x的逐渐减小,阻力系数开始减小,在x=-0.50Dn达到最小,而空泡长度及最大直径在x=0.0Dn处才开始变化,在x=-0.80Dn处降至最低.


图6 不同锥角变阻力空化器的空泡尺寸变化曲线Fig.6 Curves of variance of cavity size for the variable-drag cavitatorswith different cone angles
2.2.2 中心元件速度对模拟结果的影响
为研究中心元件的运动速度对空泡流场结构的影响,本文选取中心锥角2β=60°的变阻力空化器,对其中心元件速度uc=1 m/s时的瞬态空泡流进行了模拟计算.
图7为不同uc下的阻力系数Cd曲线,由图知2种速度下的阻力系数变化趋势基本一致:即随着工作行程值x的减小,阻力系数逐渐下降,降至最低值后不再变化,中心元件速度为1 m/s时,计算的阻力系数值要略大些.

图7 阻力系数随工作行程变化曲线,2β=60°Fig.7 Curves of drag coefficient on working stoke,2β =60°
空泡尺寸随工作行程变化曲线如图8,随着工作行程值x的减小,空泡长度Lc和最大直径Dc并没有马上减小,而是经过一段时间的迟滞才开始变化;由于与速度为0.1 m/s的计算结果相比,中心元件速度为1 m/s时得到的阻力系数值要稍微大些,故该速度下计算的空泡尺寸也有小幅增加,由于迟滞效应,1 m/s速度下计算的空泡长度在x=0.466Dn时开始增加,直到工作行程值x=-0.80Dn,2种中心元件运动速度下的空泡长度不再变化;而空泡最大直径的增加与阻力系数同步.

图8 不同中心元件速度的空泡尺寸随工作行程变化曲线,2β=60°Fig.8 Curves of cavity size on working stoke at different velocity magnitudes of central element,2β =60°
结合图7、8可以看出,中心元件运动速度地大小对变阻力空化器的空泡流模拟结果有一定影响,随着速度的增大,空泡尺寸及阻力系数值均有所增加,其中空泡长度的增加幅度最大达到了10%,而空泡最大直径和阻力系数受速度影响较小.
2.3 改进的可变侧向力空化器
2.3.1 控制方案与内部结构
上述变阻力空化器虽然可以比较快速的改变航行体阻力和空泡尺寸,然而要想获得良好的控制效果,需要其控制机构能够轻易提供数十万牛顿的力,这一控制方法很难实施.考虑到空化器侧面的压力较低,而且通过增加空化器有效面积同样可以改变航行体的受力,本文提出了如图9所示的可变侧向力空化器的控制方案:在锥形空化器内部安装一外径小于Dn的可动元件3,通过可动元件3的横向运动来控制元件2的位置,元件2、3均设计成4瓣,控制元件2内部共有8对弧形钢片4,其中每瓣的两端均有一对弧形钢片,可动元件3由锥形可动部分和圆柱操纵杆连接而成,4瓣圆柱操纵杆分别控制4瓣圆锥部分的横向位移,从而改变控制元件的周向位移hn值,使前端空化器1的有效工作面积变化,进而改变空泡尺寸;当可动元件任意两侧位移不一致时,控制元件具有不对称性,前端锥形空化器产生不对称受力,使空泡形态发生变化,可以有效的控制航行体运动姿态,有关可变侧向力空化器的具体内容可参考文献[14].


图9 可变侧向力空化器的控制方案Fig.9 Control scheme of the variable-lateral force cavitator
2.3.2 空泡流模拟结果
图10、11给出了45°锥角空化器的控制元件2上半周部分突出1/10Dn时的空泡流计算结果,由于元件2的不对称性,在空化器上产生竖直向下的升力,导致空泡上下截面不对称(如图10所示).3种空化数下得到的空化器阻力系数分别为0.620、0.553和0.544,相比于圆锥空化器,可变侧向力空化器在相同空化数下的阻力系数增加了近60%,证实了其在阻力控制方面的灵敏性.

图10 可变侧向力空化器的空泡形态Fig.10 Cavity shapes of the variable-lateral force cavitator
空化数为0.190时的空化器前端纵剖面的压力系数分布如图11所示,可以看出,凸出的元件2导致了不对称的压力分布,从而在空化器上产生了相当于30%阻力的升力,升力系数达到0.177;此外压力系数等值线显示,控制元件2外表面的压力非常低,这保证了元件的可操作性.

图11 可变侧向力空化器前端压力系数等值线,σ=0.190Fig.11 Contours of pressure coefficient in front of the variable-lateral force cavitator,σ =0.190
3 结论
本文利用FLUENT6.2的自然空化模型和动网格技术对水下超空泡航行体的瞬态空泡流进行了数值模拟,得到了以下几点结论:
1)传统变阻力空化器的阻力响应速度较快,空泡外形的变化则要滞后于阻力变化;随着工作行程值的减小,不同锥角的变阻力空化器的阻力系数和空泡尺寸也逐渐减小;
2)中心锥角越小,对应的空化器工作行程及阻力系数(空泡尺寸)的变化幅度也就越大,2β=60°时在工作行程内可得到阻力系数几乎3倍的变化;
3)中心元件运动速度对模拟结果也有一定影响,速度值从0.1m/s增至1m/s时,空泡尺寸有小幅增加;
4)数值模拟结果显示可变侧向力空化器对阻力和升力的控制非常灵敏.
[1]MAY A.Water entry and cavity-running behavior ofmissles[R].AD-A020259,1975.
[2]WOLFE wP.Drag of revolution in supercavitating flow[J].Journal of Fluids Engineering,1989,112:23-30.
[3]贾力平,张嘉钟,于开平,等.空化器线形与超空泡减阻效果关系研究[J].船舶工程,2006,28(2):20-23.JIA Lingping,ZHANG Jiazhong,YU Kaiping,et al.Research on the relation of cavitator profile and supercavity dragreduction[J].ShipEngineering,2006,28(2):20-23.
[4]顾建农,张志宏,高永琪,等.充气头型对超空泡轴对称体阻力特性影响的试验研究[J].兵工学报,2004,25(6):766-769.GU Jiangnong,ZHANG Zhihong,GAO Yongqi,et al.An experimental study about the influence of ventilated headforms on the drag characters of a super cavitation axisymmetric body[J].Acta Armamentarll,2004,25(6):766-769.
[5]贾力平,王聪,于开平,等.空化器参数对通气超空泡形态影响的实验研究[J].工程力学,2007,24(3):159-164.JIA Liping,WANG Cong,YU Kaiping,etal.Experimental investigation of cavitator parameters effecting on ventilated supercavity shape[J].Engineering Mechanics,2007,24(3):159-164.
[6]SAVCHENKO Y N.Control of supercavitation flowand stability of supercavitating motion of bodies[C]//The RTO AVT Lectures Series on"Supercavitating Flows",RTO Lecture Series 005.Ottawa:St.Joseph,2002:313-341.
[7]WAID R L.Cavity shapes for circular disks at angles of attack[R].California Institute of Technology.Report No.E-73.4,1975.
[8]SEMENENKO V N.Artificial supercavitation physics and calculation[C]//RTO/AVT lecture series on"supercavitating flows",RTO Lecture Series 005,Ottawa:St.joseph,2002:195-227.
[9]黄海龙,王聪,黄文虎,等.变攻角圆盘空化器生成自然超空泡数值模拟[J].北京理工大学学报,2008,28(2):100-103.HUANG Hailong,WANG Cong,HUANG Wenhu,et al.Numerical simulation on natural supercavity based on diskcavitator with variable attack angle[J].Transactions of Beijing Institute of Technology,2008,28(2):100-103.
[10]MANNINEN M,TAIVASSALO V,KALLIO S.On the mixturemodel for multiphase flow[M].Espoo:Technical Research Center of Finland,VTT Publications,1996:3-67.
[11]SINGHALA K,ATHAVALEmM,LIH Y,etal.Mathematical basis and validation of the full cavitation model[J].Journal of Fluids Engineering,2002,124:617-624.
[12]FU Huiping,LU Chuanjing,LIJie.Numercial research on drag reduction characteristics of supercavitating body of revolution[J].Journal of ShipMechanics,2004,8(3):1-8.
[13]SAVCHENKO Y N,VLASENKO Y D,SEMENENKO V N.Experimental study of high-speed cavitation flows[J].Jof Fluid Mechanics Research,1998,26(3):103-111(in Russian).
[14]哈尔滨工程大学.可变侧向力空化器[P].中国:20091007,2007.3,2011,4.21.

