超重型数控镗铣床精度可靠性研究

胡占齐，解亚飞，刘金超

(燕山大学机械工程学院，河北秦皇岛066004)

重型和超重型数控机床是机械制造业的重要基础制造装备，其特点是批量少、使用寿命长、维修成本高，一旦加工中出现问题造成的损失大.因此，科学地预测重型数控机床的精度可靠性，保证其服役期间的使用性能，降低维护成本是重型制造装备(maintenance，repair＆ operation，MRO)技术的重要基础环节，是精益制造思想的具体体现［1-2］，也是目前MRO技术研究中较少被关注的内容.

机械系统的可靠性还处于发展时期，现有的可靠性理论和方法主要是在电子工程领域发展起来的，带有电子工程的烙印［3］，而不同系统、不同的失效机理需要不同的模型，甚至不同的概念和定义.不加区别地直接应用传统方法与模型、或隐含地做出不合理的假设都会导致可靠性分析、评价失去价值，甚至得出错误的结论［4］.

对于数控机床的可靠性，目前大都局限于一定批量生产的中小型机床［5］.由于重型数控机床的数量较少，无法形成足够的统计样本，很难用统计学方法研究其可靠性.本文针对这一特点，将精度可靠性的概念用于重型机床可靠性的研究，以某型号超重型落地数控镗铣床为研究对象，在机床多体运动学模型基础上，提出其精度可靠性的预测模型.用精度可靠性模型可以预测机床的维护周期，机床维护周期可以作为重型机床维护、维修管理中的基本依据，也是机床MRO数据库的基本数据之一.该方法还可将MRO的范围扩展到机床的设计阶段，为机床产品的全寿命周期的优化提供了技术支持.

1 重型数控机床的空间误差模型

某型号超重型落地铣镗床的几何模型如图1所示.该铣镗床镗轴直径 320 mm，镗轴行程为1 800 mm，滑枕行程为2 000 mm，回转工作台承重500 t，是重型装备制造业的关键技术装备.由图可见该镗铣床由12个部件组成.

图1 某型号超重型落地铣镗床几何模型Fig.1 Geological module of a supper heavy m ill-bole machine tool

根据部件间的拓扑结构，可以列出其低序体阵列，再根据低序体阵列所表示的拓扑关系和各部件间的运动关系，就可以得出各部件间的理想静止、运动特征矩阵和静止、运动误差特征矩阵.例如部件1(床身)和部件2(滑台)间的理想静止特征矩阵和静止误差特征矩阵均为4阶方阵，理想运动特征矩阵和运动误差特征矩阵分别为

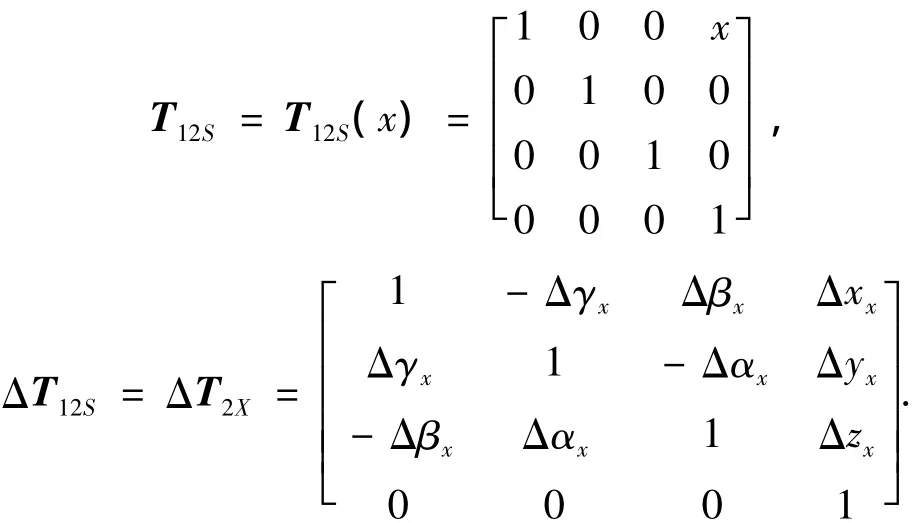
式中:x为滑台相对于床身沿x方向的位移，Δxx为滑台相对于床身沿x方向的位移误差，Δyx为滑台相对于床身沿y方向的位移误差，Δzx为滑台相对于床身沿z方向的位移误差，Δαx为滑台相对于床身绕x轴的转角误差，Δβx为滑台相对于床身绕y轴的转角误差，Δγx为滑台相对于床身绕z轴的转角误差.

列出所有部件间的理想静止、运动特征矩阵和静止、运动误差特征矩阵，可以得出刀具成型点的实际位置和设计位置之间的误差［6］:

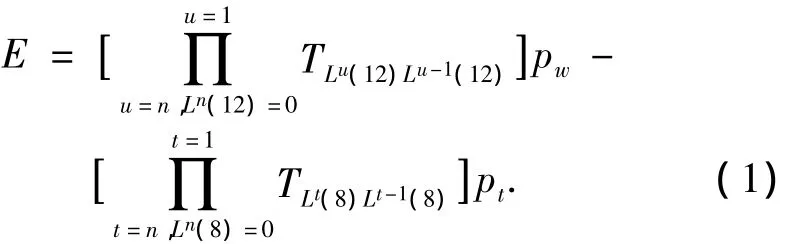
式(1)即为该超重型落地铣镗床的空间误差模型，E值的物理意义是刀具理想位置和实际位置的误差向量.其中:Pw为理想加工点在工件坐标系中的齐次坐标;Pt为实际加工点P在刀具坐标系中的齐次坐标;TuL(j)TLu－1(j)为单元体j和相邻低序体转换矩阵，在本例当中，工件所在单元序号为12，刀具所在单元序号为8.

当机床部件较多时，式(1)将非常复杂，因此实际应用过程中通常会根据研究问题的侧重点不同，并考虑各部件的磨损量对加工精度影响的不同，对式(1)做不同程度的简化.根据对上述超重型数控铣镗床工作原理的分析，认为机床主轴和滑枕对于加工精度的影响较大.为说明问题简化起见，本文仅研究主轴和滑枕对加工精度的影响，同时以考虑工件和刀具的安装误差，式(1)可以简化为

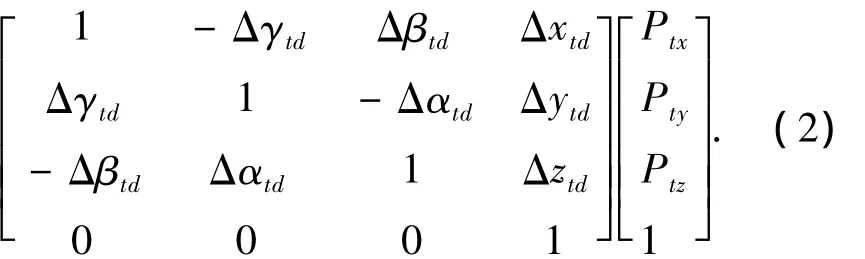
式中:脚标wd的元素为工件的安装位置及安装误差，脚标td的元素为刀具的安装位置及安装误差，脚标yC和xC的元素分别表示主轴轴承磨损引起的C轴与x轴和y轴的夹角误差，脚标z的元素表示滑枕磨损引起的z轴与其他2个坐标轴的角误差.式(2)描述了由于各种原因引起的机床部件间位置误差导致的工件加工误差，本文将以此为基础研究超重型落地铣镗床的精度可靠性以及在MRO技术中的应用.

2 运动副磨损对机床加工精度的影响

机床上有相对运动的表面间都会有磨损，但是每个运动副的磨损量对加工精度的影响是不同的，各个运动副在机床工作过程中的有效作用时间也不一样，还需考虑到加工精度敏感方向的影响，因此机床加工精度随机床工作时间的推移而变化的情况极其复杂，应该具体情况具体分析.考虑到运动副在加工过程中工作的频繁程度和对加工精度敏感方向影响的大小，这里只选择镗床的主轴和滑枕对加工精度影响较大的相对运动表面作分析，其他运动副的分析方法完全相同.

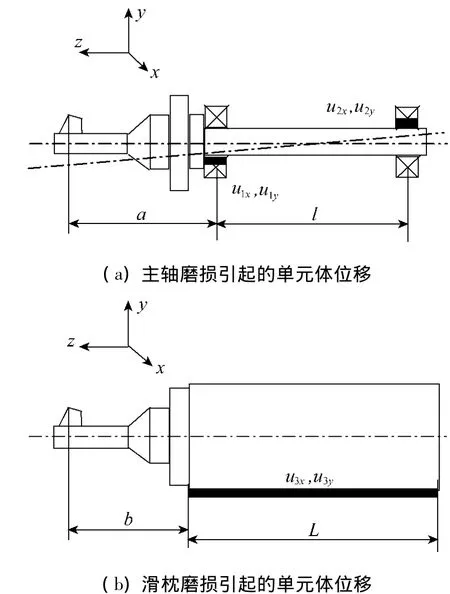
图2 主轴和滑枕的磨损导致所在单元位置的变化Fig.2 Position change of unit of spindle and slider caused by wear

图2是主轴和滑枕的磨损引起的单元体位移的示意图，而单元体的位移表现为式(2)中相应转换矩阵元素的变化.分析转换矩阵中元素随时间变化的规律，就能间接地获得机床加工精度随时间变化的规律.下面以上述误差引起的主轴位移为例，分析超重型落地铣镗床的精度可靠性.

设主轴轴承发生磨损 u1x、u1y、u2x、u2y后，引起的主轴倾斜角度为ΔαxC和ΔγyC，滑枕发生磨损u3x、u3y后，引起的滑枕相邻低序体转换矩阵中的元素变化为 ΔαZ、ΔγZ，、ΔxZ和 ΔzZ，由图(2)所示的几何关系，可以得出磨损量和转换矩阵相应元素间的关系为

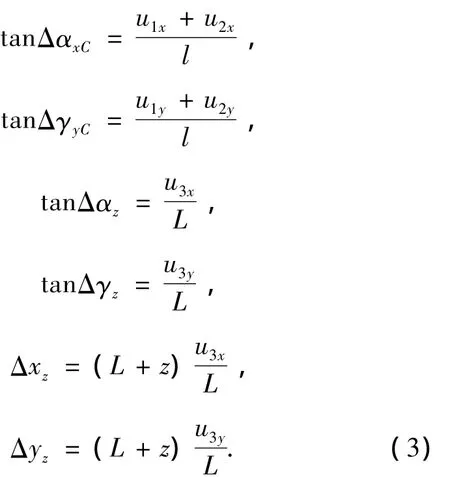
运动副间的磨损量与接触面间的法向压力以及接触面间的摩擦系数有关，接触面间的法向压力可以通过有限元方法计算，接触面间的摩擦系数可以通过运动副材料的摩擦学试验得到.一般在正常磨损期间，磨损量与摩擦路程或时间成正比，可以表示为

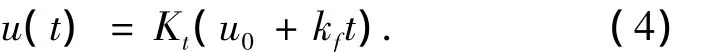
式中:u0和kf为运动副材料的摩擦学常数;Kt为运动副的有效工作时间系数，是机床工作状况的统计参数，表示某一部件工作时间占机床总的工作时间的比例.

特别要指出的是，机床种类不同，机床的加工对象不同，都会影响到加工精度的变化规律，因此要针对具体机床的具体工作情况分析加工精度的变化才有意义.

3 精度可靠性及维护周期的预测模型

将式(3)、(4)代入式(2)可以得到机床加工精度的时间函数，机床误差矢量在精度敏感方向的投影可以表示为

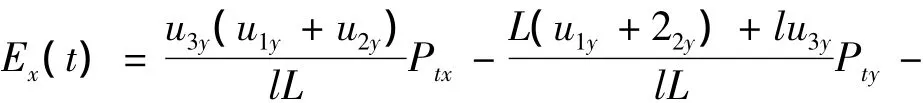
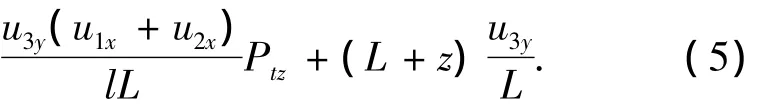
式中:uij为相应运动副间的磨损量，为时间函数，可参考式(4)得到.

精度可靠性是指机床的加工精度保持在设计加工精度范围内的可信程度，对于重型机床这类缺少足够统计样本的大型制造装备，可以用维护周期来衡量其精度可靠性.一般来说，随着机床工作时间的推移，其加工误差会逐渐增加，维护周期是指机床加工误差超出设计指标前，机床的有效工作时间，或2次保养之间机床的机动时间.将机床允许的最大误差值Ex0带入式(5)就可以求出维护周期Tc.科学有效地预测机床的维护周期，无疑是重型机床MRO技术的基本内容之一.

式(5)即所研究型号落地铣镗床维护周期的预测模型，它反映了机床的加工误差随着时间推移而变化的情况，以及机床部件间运动副磨损量和加工误差的变化情况.维护周期的概念可以用图3来说明，图中同时表示了运动副间磨损量随时间的变化、机床的加工误差随磨损量的变化和机床加工误差随时间的变化情况.若只考虑一个运动副的影响，图中第3象限表示运动副之间的磨损量随时间增加的情况，第2象限的曲线表明运动副磨损量和机床加工精度间的关系，则第1象限的曲线则表明机床加工误差随时间增加的情况.Ex0表示加工敏感方向的最大加工误差，加工误差达到Ex0之前所经历的时间Tc即为机床的维护周期.如果将机床考虑成线性系统，则总的误差应为每个运动副引起的加工误差之和.

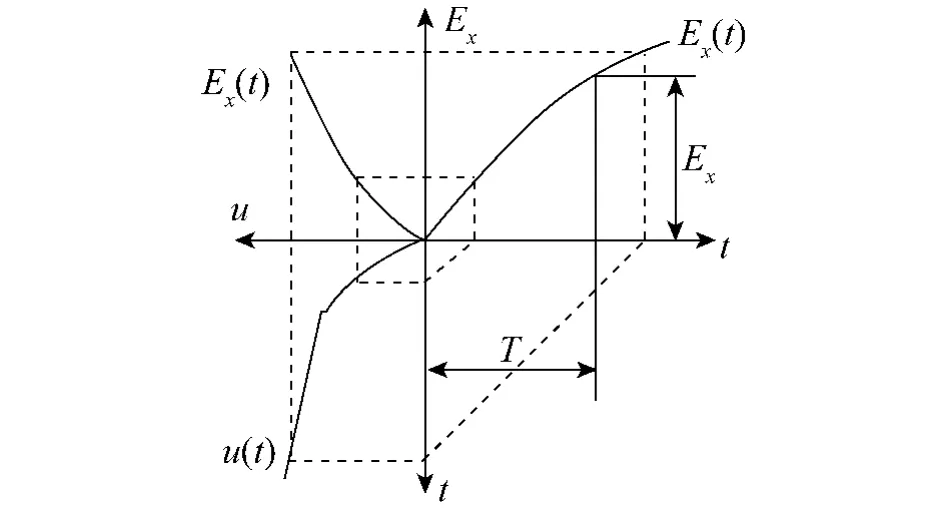
图3 机床维护周期的预测模型Fig.3 Predicting module ofmaintenance cycle of machine tools

特别要考虑的是，每个运动副的磨损量都是随机变量，由此得出的机床加工误差也是随机变量.运动副磨损量的均值和方差可以由摩擦学实验得到.一般认为各随机变量均按正态分布，加工误差的均值和方差可以按下面的方法求出.

将加工误差按照泰勒级数在磨损量均值处展开，忽略二阶及以上导数的高次项，得到各摩擦副误差引起的加工误差为

由这些参数引起的加工误差的均值和方差可表示为

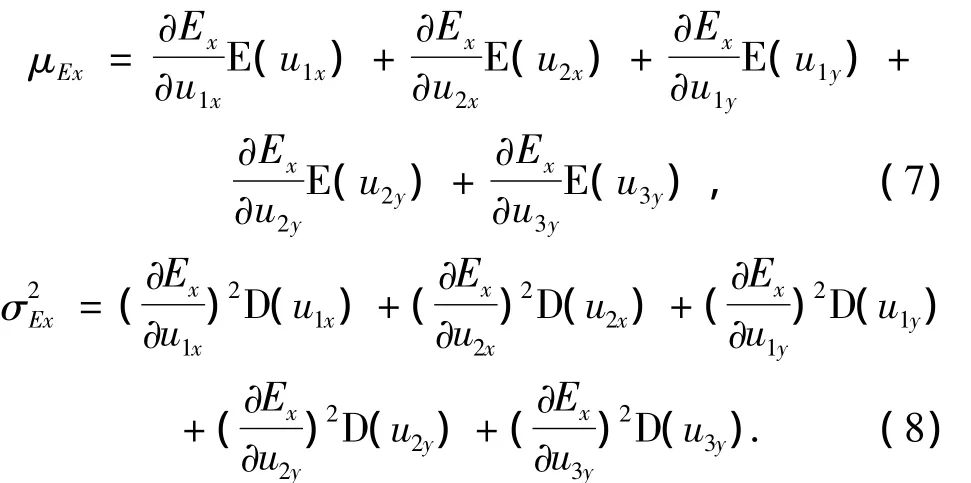
式中:E(*)表示随机变量的均值，D(*)表示随机变量的方差.为了准确地预测机床的维护周期，必须知道数学模型中的各项参数的准确数值，其中包括运动副的摩擦学特性，机床运动副间的受力情况.运动副的摩擦学特性可以通过相同材料的摩擦学试验获得，而运动副间的受力情况可以通过有限元方法准确计算出来，因此重型机床维护周期的预测是可行的.该方法的意义还在于，在机床的设计阶段就能够对机床的精度可靠性进行预估，以利于用最少的成本和最短的时间制造出符合要求的产品.同时这一方法将MRO技术延伸到产品的设计阶段，实现了机床产品的全生命周期的优化设计，这对于单件小批量生产的重型数控机床产品无疑具有非常重要的意义.

机床结构比较复杂时，理论计算非常复杂，实际中也可以用统计模拟方法也称蒙特卡罗方法来实现精度可靠性的预测.

4 运动副初期磨损的预测

运动副磨损过程的重要特点之一是存在着初期磨损阶段也称磨合期.在磨合期内，磨损量与时间之间呈现非线性关系，这是进行精度可靠性评估和预测时必须注意的特点.产生磨合期现象的原因大致可以归纳为零部件的制造误差、工作中的受力变形和摩擦过程中的接触条件3个方面［7］.下面以所研究的铣镗床中部件1和部件2间的初期磨损阶段为例做简要说明，图4表示了在磨损初期的接触情况.由于制造精度和载荷的影响，造成导轨工作面接触不良.假设导轨面仍为平面，θ表示实际接触面的倾斜角，在磨合期内实际接触宽度小于名义接触宽度，B＜B0，设导轨长度为L，则摩擦表面的压强与磨损量的关系为

当磨损与压力及速度成线性关系时，有

将式(9)代入式(10)并积分得

式(11)说明在初期磨损阶段，磨损量和时间成非线性关系.

令u=u0=B0tanθ，可得磨合期为

式(12)说明耐磨性好的材料(kf较大)，需要的磨合期较长.式(12)是预测磨合期的基本方程.磨合期结束时，通常要对机床做一次调整.进入正常磨损阶段后，磨损量与时间将成如式(4)所示的线性关系.这时，产生与磨合期同样的磨损量，经过的时间将是磨合期的2倍.

图4 导轨的初期磨损阶段Fig.4 Earlier wearing period of slider

5 实例分析

设某超重型落地铣镗床滑枕移动200 mm，2个运动副处的摩擦系数均值分别为0.06和0.08，方差均为0.01，有效工作时间系数分别为kt1=kt2=kt3=1，摩擦学常数u01=u02=u03=0，滑枕行程及铣轴伸出量l=L=1 000 mm，在工件坐标系和刀具坐标系内取一相同点 p(1，2，3，1)T，将式(3)代入式(2)可得:

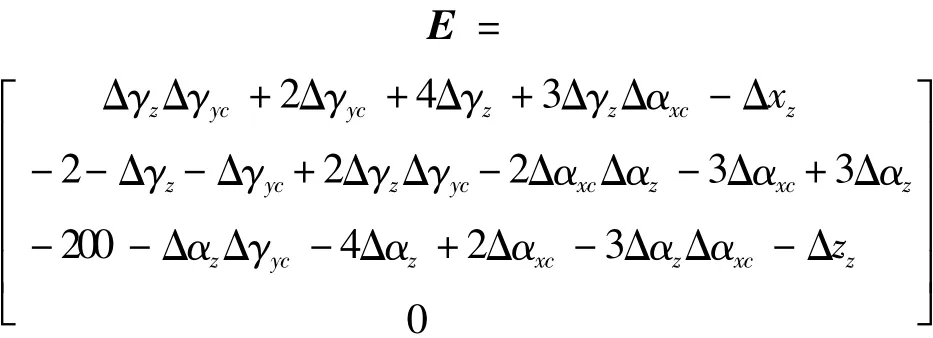
可令:

得

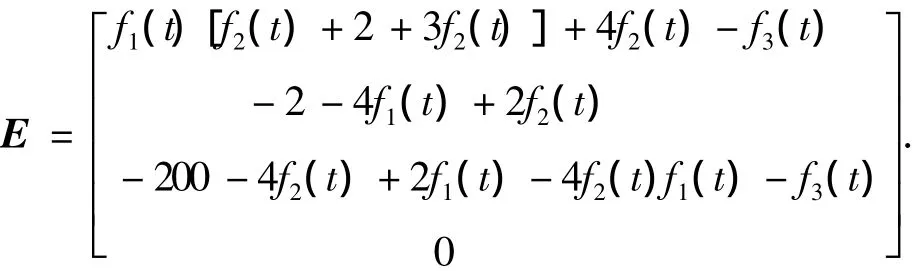
参照标准 JB/T 8490.1 － 96［8］，得到精度各个方向的平均允差均为0.01，方差均为0.01，则各个方向的可靠度为

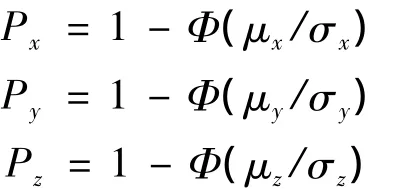
对机床的精度保持性能进行分析，如图5所示.

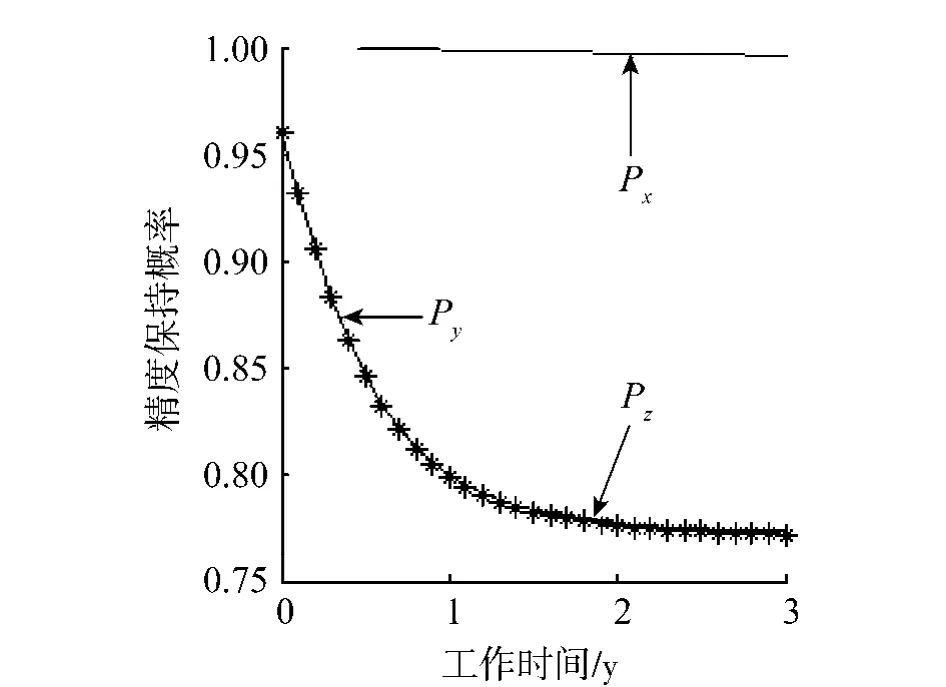
图5 机床精度保持概率Fig.5 Precision probability of machine tools

通过对结果的分析可知，x、z方向的误差对加工精度保持性能的影响最大.工作1年时间内精度保持性能变化比较大，随后平缓上升，具体的维修周期根据各个厂家的不同Tc值而定.

6 结论

MRO技术不仅是机床使用过程中的管理问题，对于重型数控机床而言，在设计阶段就尽可能地考虑到保养、维修和运行问题，实现重型数控机床的全寿命周期的优化设计，对提高重型数控机床的质量、降低成本具有重要的意义.

对于难以用统计学方法进行可靠性研究的重型数控机床来说，建立精度可靠性的数学模型，进行维护周期的预测，具有较大的实用价值.数学模型的准确性取决与机床运动副的摩擦学特性和机床部件间的载荷计算的准确性.

误差对于某一运动副的导数反映了这一运动副的磨损量对于机床加工精度影响的程度，因而精度可靠性的数学模型还可用于误差源的分析，帮助设计者找出对加工精度影响最大的因素，然后改进设计，提高机床的性能.

［1］詹姆斯.P.沃麦克，丹尼尔.T.琼斯.精益思想［M］.沈希瑾，译.北京:商务印书馆，2003:254-256.WOMACK J P，JONES DANIEL T.Lean thinking［M］.SHEN Xijin.Beijing:Shangwu Press，2003:254-256.

［2］LUKE TM，CHAN SP.Economic analysis in the MRO industry:an options approach［J］.The Engineering Economist，2004，49(5):21-41.

［3］谢里阳，王正，周金宇，等.机械可靠性基本理论与方法［M］.北京:科学出版社，2009:3-9.XIE Liyang，WANG Zheng，ZHOU Jinyu.et al.Theory ＆method of mechanical reliability［M］.Beijing:Science Press，2009:3-9.

［4］CONNER P D T.Reliability——Past，present，and future［J］.IEEE Transactions on Reliability，2000:1-6.

［5］肖俊，胡伟，鲁志政.数控车床故障率的可靠性分析［J］.现代制造工程，2006，12:14-16.XIAO Jun，HU Wei，LU Zhizheng.Analysis of failure of CNC Lath［J］.Modern Manufacturing Engineering，2006，12:14-16.

［6］李圣怡，戴一帆.精密和超精密机床精度建模技术［M］.长沙:国防科技大学出版社，2007:54-58.LIShengyi，DAIYifan.Precision modeling of precision ＆super-precision machine tools［M］.Changsha:Defense Science＆ Technology University Press，2007:54-58.

［7］四川省机械工程学会编译.机器可靠性［M］.成都:四川人民出版社，1983:380-390.Sichuan Mechanical Society.Reliability of machine［M］.Chengdu:Sichuan People Press，1983:380-390.

［8］中华人民共和国机械行业标准.落地镗铣床、落地镗铣加工中心精度检验［S］.JBT/8490.1-96，1996:3-9.Mechanical Engineering Standard of China.Precision test of floor type boring and milling machine tools［S］.JBT/8490.1-96，1996:3-9.

［9］KEN TR.An enterprise approach to total life cycle systems management［EB/OL］(2011-05-10.)http://www.osd.atl.mil/UCMC.PPT.Apr.15.2004.