基于概率算法的混流式水轮机转轮叶片组合优化模型

李文俊，陈 娟，刘 进

（东芝水电设备有限公司，杭州 311504）

水轮机转轮静平衡是转轮制造过程中的重要组成部分，通过静平衡可以消除因转轮重量不平衡产生的不平衡力矩对水轮机振动的影响，确保水轮机安全、稳定运行[2]。而要保证转轮厂内静平衡时偏心车削尽量少，关键的步骤需在组焊转轮各叶片时，根据各叶片重量进行组合排序，以使得组合后不平衡力矩最小。若叶片数量少时，可采用完全枚举法，利用排列组合的方法，找出不平衡力矩最小的组合方式这一最优解。但枚举法枚举时间随叶片个数增加成指数增长，所以该算法需要极长的运行时间与极大的存储空间，以致根本不可能在现有计算机上实现，即所谓的 “组合爆炸”。对于大规模此类问题，人们至今仍未找到完美的求解方法，只能通过各种优化算法求得一定精度内的近似解，在合理的运行时间内使其更接近最优解[3]。

传统方法处理叶片优化组合时，根据各叶片重量人工对称布置叶片，并根据雷达图手动调整，以期获得静平衡力矩最小的排列组合，人工进行数据处理，计算工作量大，工作内容不断重复。本文提出在Visual Basic环境下采用基于概率算法寻求最优解的组合优化设计模型，在计算过程中引入随机数，以提高搜索寻优的速度，并使在合理运行时间内求出满意解成为可能。

1 基本理论

叶片组合优化问题同著名的旅行商问题（Traveling Salesman Problem，TSP）一样，是一个典型的组合优化问题，易于描述却难于求解，是个 NP complete（non-deterministic polynomial complete）难题[3]。从完全图的意义上来说，该问题实际上也是图论中的最小Hamilton圈问题[4]。转轮叶片组合问题可描述为：给定n张叶片及各个叶片的质量mi，各叶片质心分布半径为R，求使其不平衡力ΣM矩最小的叶片组合方法。

混流机叶片质量分布不均匀而产生离心力。转轮运转过程中必然产生惯性力，从而在转动副中引起附加动压力，这种不平衡离心力作用在轴承上会引起振动。所以在计算中使用转轮的静不平衡力矩作为设计目标。

不考虑转轮上冠、下环的情况下，我们来考虑叶片组合对转轮静不平衡的影响。假定有N个叶片，在N个位置，按照排列组合原理，可能的排列组合一般应为PN=N×（N-1），…，×1，由于是环形布置，彼此之间顺序相同的组合即可认为是相同的组合，此时排列组合应为P （N-1） = （N-1） × （N-2）， …， ×1[5]。 现假设每个叶片的质量为mi和质心分布半径为R，对于上述任意组合，可由下式计算出转轮静不平衡力矩：

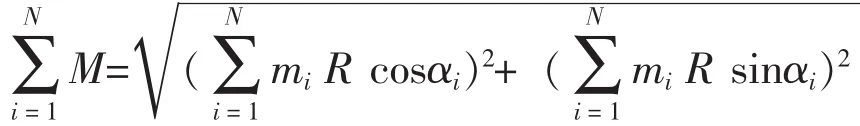
2 优化模型

这里讨论在VB环境下以概率算法寻优的模型，对叶片的可能的情况进行搜索，在合理的运行时间内搜寻令人满意的最优解。

Visual Basic 6.0作为一款可视化、面向对象和采用事件驱动方式的结构化高级程序设计语言，可用于开发Windows环境下的各类应用程序，具有简单易学、效率高、功能强大、交互性和兼容性强等特点[6]，因此选择VB作为优化设计模型的程序开发工具。

2.1 概率算法

相对于精确算法的每一个计算步骤都是固定的而言，概率算法允许算法在执行的过程中随机选择下一个计算步骤。许多情况下，当算法在执行过程中面临一个选择时，随机性选择常比最优选择省时。因此概率算法可在很大程度上降低算法的复杂度。在许多情况下，要计算出问题的精确解是不可能或没有必要的，因此用概率算法可得到相当满意的解。概率算法的搜索寻优过程具有随机性，不断扩大搜索范围，容易得到全局最优解。因此，数值概率算法已被成功地应用于许多领域中。

2.2 优化程序分析

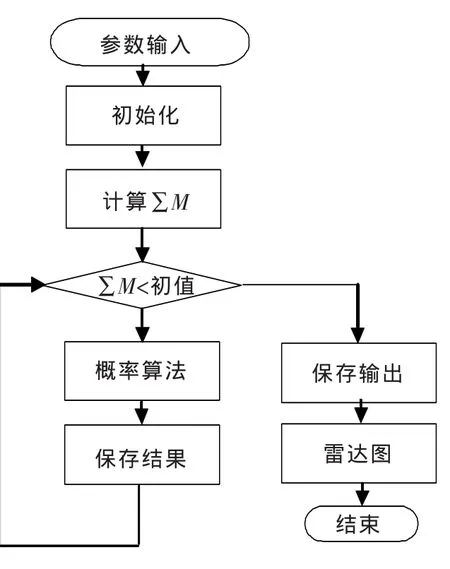
图1 概率算法流程

概率算法虽然所得到的是近似解，但近似解的精度随计算次数的增加不断提高。假设现将叶片所有可能的排列方案按从优到差进行排序。假设概率寻优得到满意解的概率为0.01%，显然每次随机方案只有0.01%的概率符合要求；但若进行10万次概率寻优，则会有99.995%的几率得到满意解。由上述分析知，概率算法寻优方案完全能保证在合理的运行时间内搜寻到满意解。

2.3 设计变量

由上述理论分析知，此程序需包含的主要参数为：叶片数量n_blade，叶片重量arr_blade（），运算次数random_times。这些参数由输入界面进行手工输入。因为叶片重量为系列值，定义为数组型，用于存储初始状态的叶片序列。为便于存储概率运算寻优过程中对各叶片的不同排序方式，再定义另一arr_patern（）数组，存储概率运算后的叶片序列。

为便于计算各叶片力矩在+X、+Y轴上的分量，分别定义数组arr_sin（）、arr_cos（）存放叶片质心与X轴夹角的正弦值和余弦值；定义数组arr_cos_m （）、arr_sin_m （） 存放叶片在+X、+Y轴力矩分量。

其中arr_sin（）、arr_cos（）可采用循环语句进行赋初值，语句如下：

for i=1 to n_blade

arr_sin （i） =sin （2× （i-1）*PI/n_blade）

arr_cos （i）=cos （2× （i-1）*PI/n_blade）

next

VB程序中计算正弦值和余弦值时，角度必须采用弧度制，所以在赋值时注意采用如下公式进行角度与弧度转化：将π定义为常量，赋值为PI=3.1415926。

力矩公式为M=mi×R，其中mi为叶片质量，R为叶片质心距转轮中心距离。各叶片力矩在+X、+Y的投影由公式计算：

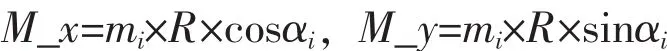
可采用如下公式进行赋值：

for i=1 to n_blade

for j=1 to n_blade

arr_sin_m（i， j）=arr_w（i，1）×arr_sin（j，1）

arr_cos_m（i， j）=arr_w（i，1）×arr_cos（ j，1）

next j

next i

2.4 目标函数

2.5 程序界面

参数及目标函数定义完全后，进行程序界面设计。本程序输入界面如图2所示，该界面包括叶片数量和运算次数输入选项。为便于输入、输出各叶片重量排列顺序，本程序采用VB中的Spreadsheet控件。

图2 输入界面

3 计算实例及分析

为验证上述优化模型的准确性，本算例采用东芝水电设备 （杭州）有限公司在制的某混流式水轮机转轮的基本数据。该机组转轮叶片数量为13只，叶片重量分别为 3597、3574、3570、3594、 3592、 3608、 3608、 3616、 3602、 3634、3574、 3609、 3575， 单位为kg。

各参数输入程序后 （见图3），程序会根据输入叶片数量，自动调整控件spreadsheet1显示的范围，并将spreadsheet1中第一列自动列出叶片序列编号。

本例通过9999次数概率算法运算，将最优结果及对应排序后的叶片编号输出至spreadsheet2中 （如图4所示），并可根据此叶片排序组合输出雷达图 （如图5所示）。由运算结果可以看出，经过9999次概率运算寻优，最终转轮叶片的静平衡力矩为0.24。传统手动排列时只要满足<1即为满意解，且为寻求此满意解，往往需要2～3天时间。而应用本优化程序，寻求此满意解花费时间仅需2min。由此验证本优化模型，请算法可以在合理的运行时间内寻求到满意解。

图3 参数输入后界面

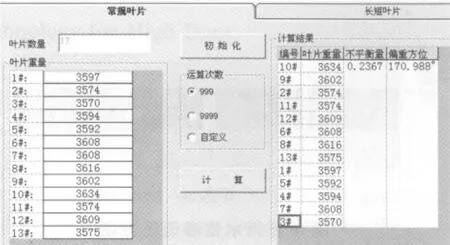
图4 优化运算结果

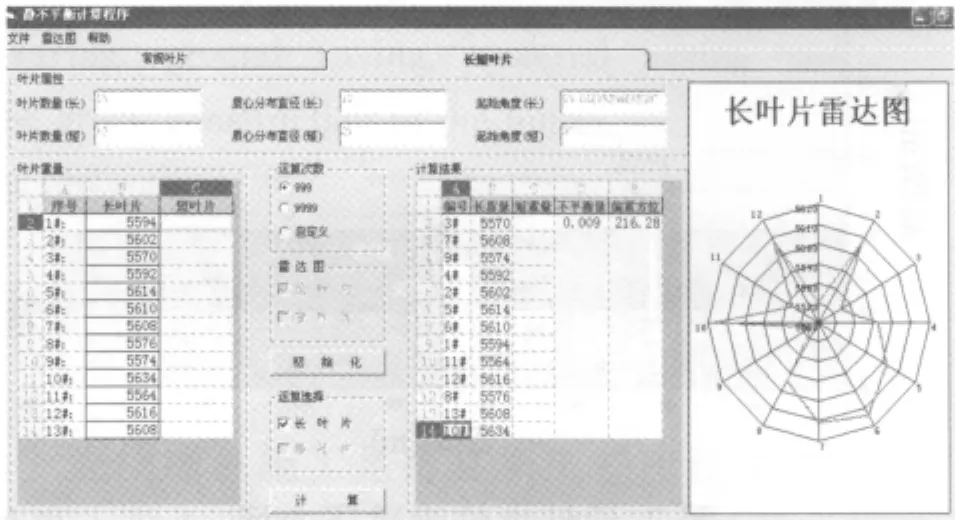
图5 雷达图显示结果

4 结语

本文提出了应用概率算法的混流机转轮叶片组合优化模型，与传统方法的对比可以看出，本模型的计算精度和效率均有很大提高，证明了其在求解此类问题上具有切实的可行性。

本模型仅考虑了概率寻优的方法，若能在寻优算法中结合诸如遗传算法、模拟退火算法、贪婪算法等启发式搜索算法，则优化程序在精度、效率上将会有更大提高。

[1] 巫发明,王立鹏,杨从新,等.基于遗传算法的直叶片垂直轴风力机风轮优化设计[J].西华大学学报（自然科学版）,2009,28(5):36-39.

[2] 许辉,王维平.三支点称重式压力传感器静平衡法及其在转轮静平衡中的应用[J].东方电机,2009，(3):13-18.

[3] 朱献文,李福荣.求解旅行商问题的几种智能算法[J].计算机与数字工程，2010，(1):32-35.

[4] 马良,王龙德.旅行商问题的一个精确算法[J].上海机械学院学报,1991,13(1):103-109.

[5] 谢伟.五叶调距桨的桨叶优化组合及整桨静平衡方法研究[J].舰船科学技术,2004,26(5):7-10.

[6] 张树兵,戴红,陈哲.Visual Basic 6.0入门与提高[M].北京:清华大学出版社,1999.