电力系统稳定器在喜河水电站的应用研究

申吴刚，董开松

（1.陕西汉江投资开发公司喜河水力发电厂，陕西 石泉 725271； 2.甘肃电力科学研究院,兰州 730050）

近几年，自并励静止可控硅微机励磁方式在同步发电机组上得到了广泛应用，该方式最大的优点是缩短了励磁调节器的时间常数，提高系统响应速度。但这种快速励磁系统由于大大减小了整个励磁系统的时间常数，使系统阻尼降低，导致系统抑制自身振荡的能力下降。根据国内外的相关研究及实践，目前消除互联电网负阻尼低频振荡最经济有效的方法就是投入电力系统稳定器（PSS， Power System Stabilizer)[1-4]。

喜河水电站安装3台60MW轴流转桨式水轮发电机组，励磁系统为自并励励磁方式，采用广州电科院生产的EXC9000微机励磁调节器，其主通道（电压调节）采用PID调节，附加励磁控制为以发电机电功率和角速度作输入信号的PSS。由于电站远离负荷中心，处于陕西南部电网330kV互联系统的弱联络线上，但同时它又是该系统的重要联络点。随着电网系统规模的扩大和快速励磁系统的大量采用，系统的正阻尼变弱，致使联络线上极易出现功率低频振荡，影响电网的安全稳定运行。本文通过建立PSS模型、整定PSS参数，以及对发电机励磁调节器相频特性的测量，验证PSS对电网低频振荡的抑制作用。

1 水轮机PSS模型

采用中国电力科学研究院的 “电力系统分析综合程序”，利用其中的自定义建模功能建立了喜河水电站3号机组的PSS模型，如图1所示。考察研究了运行年大方式，并以此为基础进行了PSS参数整定计算，计算结果见表1。

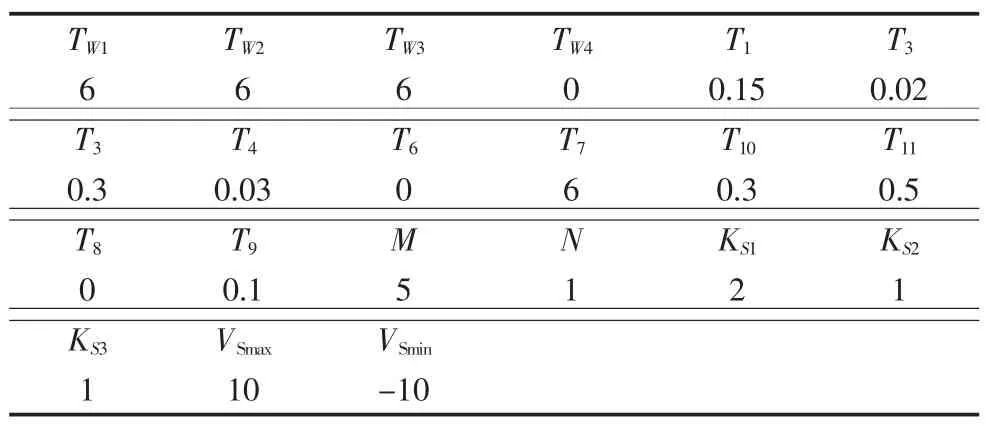
表1 电站3号机组PSS模型参数

喜河水电站3号机组的PSS模型为标准的IEEE PSS2A模型，输入为电功率和角速度，经过隔直、放大、超前滞后校正，输出到励磁调节器的电压叠加点，可以正确地区别功率正常调整与波动。它是EXC9000系统的一个标准功能。这个功能包含于测量单元板 （MUB）的软件中。附加的反馈信号为机组的加速功率 （由电功率信号ΔP和转子角频率信号Δω综合而产生的），这种模型可以克服单纯的以ΔP为信号的PSS产生的反调现象，当原动机功率发生变化时，靠Δω与ΔP通过KS3放大综合计算，然后与ΔP信号进行叠加，将原动机功率变化量抵消，PSS不输出控制信号，避免出现反调。

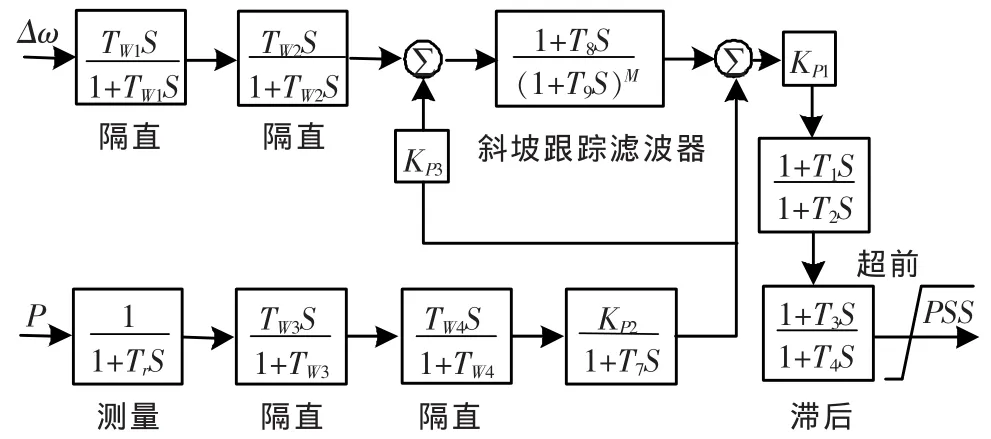
图1 喜河水电站3号机组PSS模型

图1中，TW1、TW2、 TW3、 TW4为隔直环节时间常数；T1、T2、T3、T4为超前滞后时间常数；T7为惯性时间常数；T8、T9为陷波器时间常数。

2 试验结果及分析

2.1 励磁系统滞后特性测量 （无补偿特性）

试验条件：有功功率P=52.696MW，无功功率Q=5.115MVar，机端电压U=10.361kV，功率柜单柜自动运行，退出PSS功能，定子电压接入频谱仪输入通道2，把频谱仪输出信号加在电压控制器上，电压控制器把该信号迭加在给定电压上，手动逐步增加频谱仪输出信号电平，记录输入信号与定子电压之间的频率特性。结果见表2。

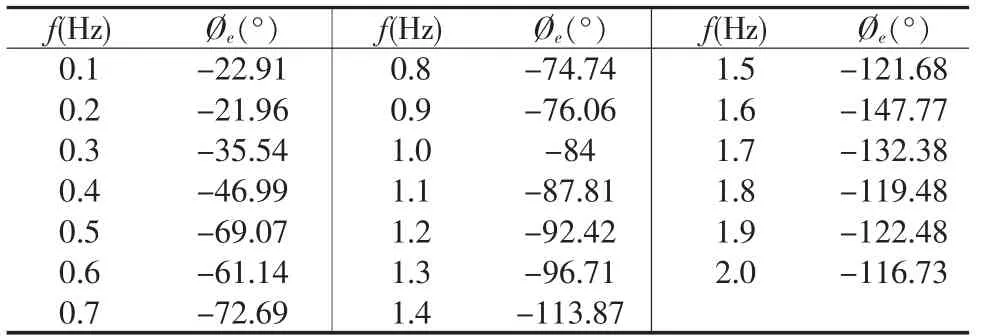
表2 电站3号机组励磁系统频率特性

2.2 PSS相位补偿特性及参数整定

喜河水电站PSS输入信号为转速和电功率，分别经两级隔直环节后再经二级超前滞后环节组成。PSS的参数整定应使PSS在0.1～2.0Hz的频率范围内提供尽可能大的正阻尼力矩。我们用覫e表示励磁系统相位、覫PSS表示相位，那么PSS参数应使得在低频 （0.1～2.0Hz）之间的 覫e+覫PSS（即有补偿特性） 在－80°～－135°之间。

有了PSS模型、励磁系统频率特性和PSS整定原则，采用逐步逼近法可以得到PSS参数如TW3=6,TW4=0,T1=0.15,T2=0.02,T3=0.3,T4=0.03。

根据图1的模型和上面的参数，计算可得到PSS环节的有补偿相频特性，见表3。

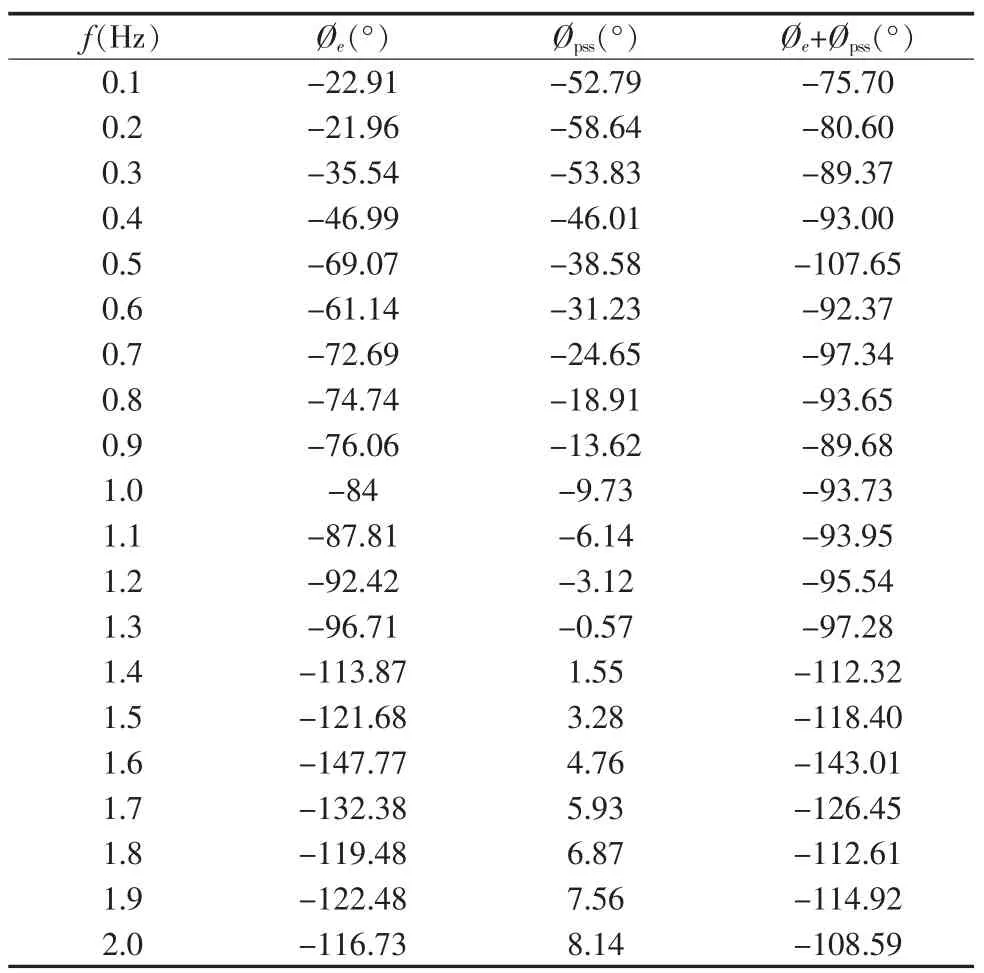
表3 电站3号机组PSS相频特性

从表3可以看出：当频率在0.2Hz到2Hz的范围内时，PSS所产生的电磁力矩对应滞后70°～150°之间，即PSS在0.1～2Hz频率范围内可以提供正的阻尼力矩。

2.3 PSS增益调整

由于电力系统是一个复杂的系统，PSS增益的理论值和实际值之间有较大的差异。在实际中增加PSS的增益不仅增加了机电振荡的阻尼，同时也可能产生电磁振荡的负阻尼，引起励磁电压和无功功率的振荡，从而导致系统的不稳定现象。因此，PSS的实际最大增益必须通过实际的现场试验来确定。

具体现场试验方法是：选定相位补偿，缓慢增大PSS增益，进行负载阶跃试验[5]，同时注意观察发电机励磁系统，当发电机转

子电压出现频率较高的剧烈振荡时，记录对应的PSS增益就是最大增益。针对喜河水电站的IEEE PSS2A模型实际增益就取试验所得增益的1/2到1/3。图2为喜河水电站3号发电机PSS增益增大为KS1=10、KS2=1、KS3=1时的波形图，此时发电机励磁电压 ULD及无功功率Q变化较大，实际运行的增益取KS1=2。

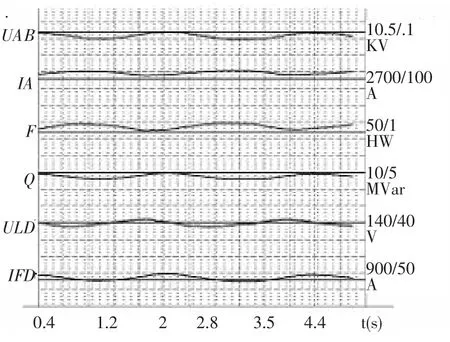
图2 电站3号机组PSS临界增益波形

2.4 PSS校核

分别在PSS投入和退出两种工况下进行发电机±3%负载阶跃响应试验，对试验结果进行对比，验证PSS的效果。试验波形如图3和图4所示。

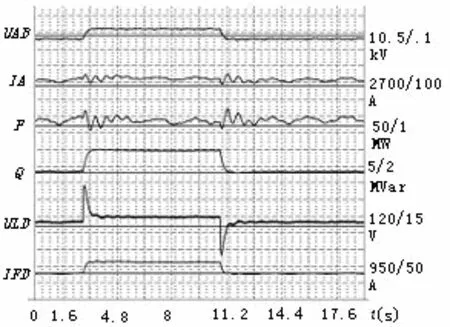
图3 无PSS时3号机组3%负载阶跃波形

多个频率叠加后，有功功率P会产生非对称波动，在图4中，PSS投入的情况下尤为明显。阻尼比采用峰峰值的计算方法：

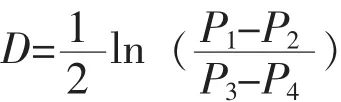
从表4可以看出，PSS投入后，增加了系统的阻尼比，提高了机组抑制系统低频振荡的能力。从PSS投入和退出的波形对比来看，PSS抑制本机振荡的效果还是比较明显的。试验结果满足DL/T650-1998标准要求。

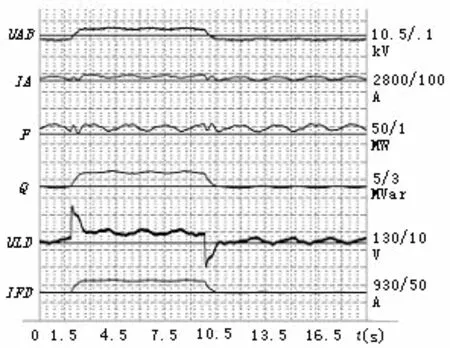
图4 有PSS时3号机组3%负载阶跃波形

表4 投退PSS效果对比

2.5 PSS投退及反调

PSS的原理是通过调整励磁系统来抑制有功功率的低频振荡。当系统正常时，PSS功能的投入会引起励磁电压的波动，但只要所引起的无功波动小，就不会影响机组和系统的正常运行。现场进行PSS的投入和退出试验，监视发电机励磁电压和无功功率的变化，未见异常，试验波形如图5所示。

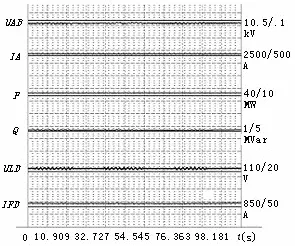
图5 电站3号机组PSS投退试验波形

在水轮机功率发生变化时，如果PSS不能区分这种变化，而把这种变化认为是系统波动，还继续作用于励磁系统，就会造成无功功率和有功功率朝相反的方向波动，也就是反调。喜河水电站3号机组PSS采用的是以电功率和转速的合成功率作为输入信号的PSS2A模型，能有效抑制反调。从图6可以看出，在有功功率快速变化的过程中，无功功率基本无反调现象。

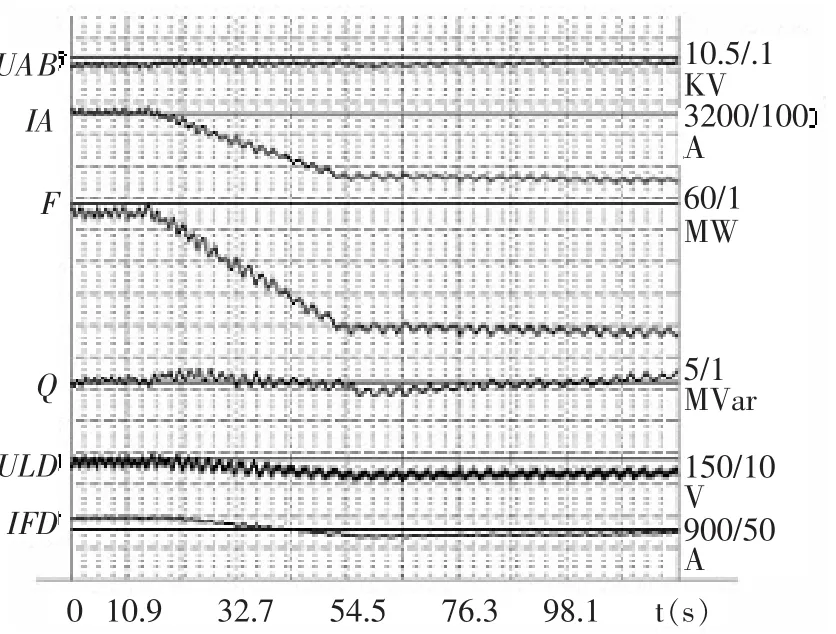
图6 电站3号机组反调试验波形

3 结论

本次试验完成了喜河水电站3号机组励磁系统模型参数测试，建立了励磁控制系统空载阶跃响应仿真模型。该模型及其参数可供调度运行部门在进行电力系统稳定分析计算中使用。

测试结果表明，喜河水电站3号机组励磁系统性能满足国家标准要求，其PSS能正确补偿相位，增加系统阻尼，明显加强了机组对于本机振荡的阻尼作用，可长期投入运。同时其PSS的投入对于西北电网可能出现的0.2～0.5Hz区域间低频振荡具有较好的抑制作用。

[1]李强,袁越,周海强.浅谈电力系统低频振荡的产生机理、分析方法及抑制措施[J].继电器,2005(9):78-84.

[2]郝思鹏.电力系统低频振荡综述 [J].南京工程学院学报(自然科学版).2003(1):1-8.

[3]韩慧云,黄梅.电力系统低频振荡与PSS分析[J].华北电力技术,2005(7):1-4.

[4]李基成.现代同步发电机励磁系统设计及应用 [M].中国电力出版社,2009.

[5]方思立,谭有信,黄文灵.电力系统稳定器参数计算及调试方法[J].中国电力,2000(6):29-32.

[6]沈利平,付廷勤,王茂元.PSS模型比较及反调试验的应用[J].水电站机电技术,2008(12):89-92.