基于详细化学动力学的AP气相数值模拟①

赵 瑜，鲍福廷，胡声超

(西北工业大学航天学院，西安 710072)

0 引言

AP是目前固体火箭发动机燃料中广泛采用的氧化剂，因为它具有与其他组分相容性好、气体生成量大、生成焓大、吸湿性较好、成本低、各项性能都较好等优点。与其他固体燃料一样，AP气相燃烧模型的发展同样经历了3个阶段［1］:

(1)总体动力学模型。该模型出现于20世纪60～70年代，只求解能量方程，并采用了火焰面假设。

(2)准总体动力学模型，即包含几个有限化学反应的模型。该模型产生于20世纪70～80年代，其弱化了火焰面假设，并同时求解能量和组分方程。

(3)详细化学动力学模型。其抛弃了火焰面假设，并包含多个有限化学反应，同时通过求解完整的N-S方程，来得到火焰结构和组分浓度、速度、密度等在求解域内分布。

目前，国外已对多种常用固体推进剂建立了详细化学动力学模型，但国内在这方面还是空白。遇到的主要问题有:

(1)详细化学动力的引入，将导致控制方程的刚性严重。其直接后果就是只能采用很小时间步来推进，使得求解耗时过长。

(2)固体推进剂燃烧时，燃面处火焰区域属于低马赫数可压流范围。因此，空气动力学中适用于求解高速流动的可压流计算方法不再适用，需做一些特殊处理。

(3)固体推进剂燃烧时，燃面处火焰区域压力波动十分微小。如利用一般的N-S方程，这种微量的波动，将导致求解困难，甚至得不到收敛结果。

针对以上难题，本文分别采用了以下方法:

(1)并行计算。通过缩减方程每次迭代所需的时间，从而显著地加快了得到收敛结果的过程。

(2)预条件化处理。通过在原始方程两端乘以特定的矩阵，使传统的可压流计算方法适用于低马赫数区域。

(3)涡速方程。通过涡量的引入，使压力波动项在方程中消失，避免了微小压力波动对收敛的负面影响。经过上述方法，AP气相燃烧的详细化学动力学模型最终被建立，并与实验结果进行了比较。

1 模型描述

1.1 控制方程

涡速方程由N-S方程变形而来，相当于用涡量替代了压力项，更适用于求解压力波动微小的燃烧问题，特别是对求解固体推进剂燃烧这类火焰结构十分微观的模型十分有利。其方程如下:

上述方程建立在二维柱坐标系下，其中vr为径向速度;vz为轴向速度;w为涡量;ρ为密度;μ为粘性;V为速度矢量;g为重力加速度矢量;cp为定压比热容;T为温度;λ为热导率;Y为质量分数;为扩散速度;h为焓;W为相对分子质量;为反应速率;

1.2 计算网格和边界条件。

在二维柱坐标系下，计算网格取为4×25，径向4个节点，轴向25个，且沿轴向网格在燃面处有加密，具体如图1所示。AP燃烧本质是一维预混燃烧，这里选取二维柱坐标系的原因是为以后扩散燃烧做准备。因此，图1中网格径向长度的选取可随意，轴向长度的选取要根据计算结果来确定。

图1 网格示意图Fig.1 Mesh example for AP

边界条件的确定如下:

对左右边界:

出口边界:

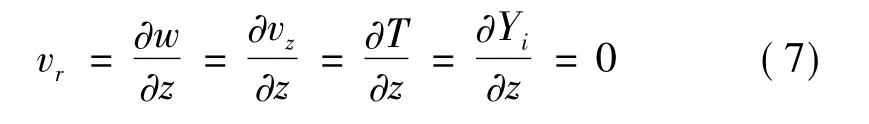
入口边界:

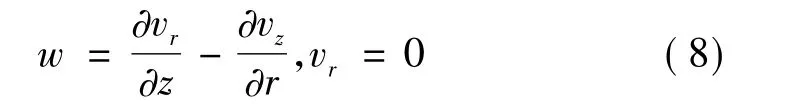
其他入口参数取自Ermolin［2］的试验数据，其AP燃烧的表面温度约800 K，处于0.6 atm下，入口组分摩尔分数见表1。

1.3 差分格式。

模型采用有限差分法求解，对一阶差分:

二阶差分:

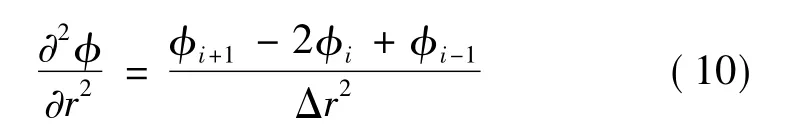
二阶差分中含变量的采用如下格式:

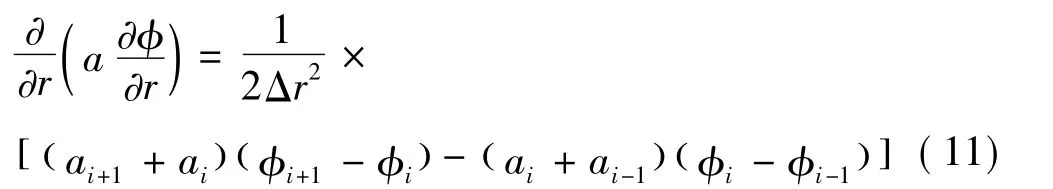
交叉的二阶差分采用:

1.4 反应方程

模型中所采用的有限化学反应方程见表2［3］。

表1 Ermolin的AP燃烧试验数据Table 1 Experiment data for AP at inlet from Ermolin

表2 AP气相燃烧反应方程Table 2 Reactions for AP in gas phase

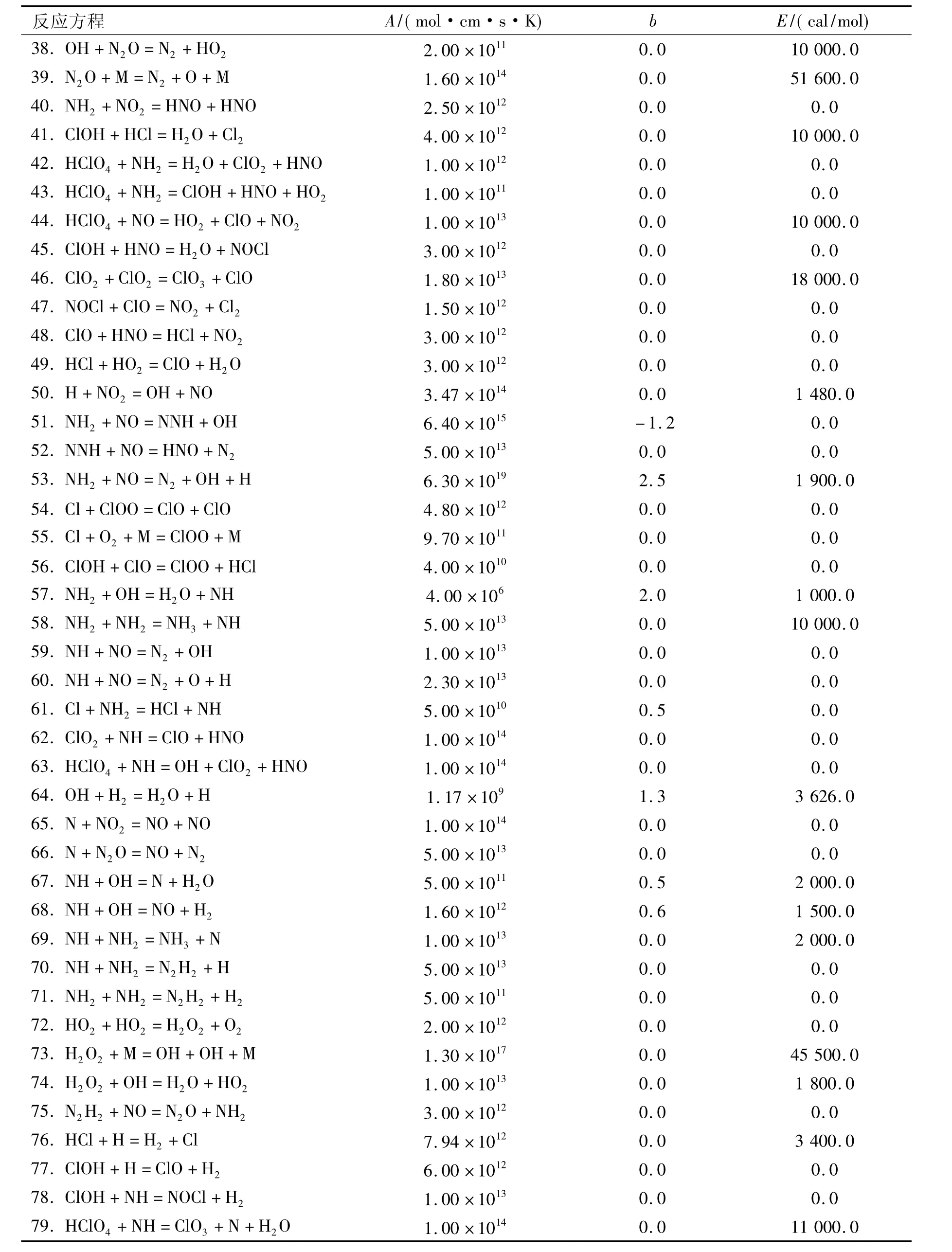
续表2Table 2 (continued)

以上79个反应方程共包含29个组分。

模型求解的代码建立在PETSC［4］上，PETSC全称为便携可扩展科学计算工具库，对求解大型偏微分方程组十分有效，提供各种常用预条件化处理格式，支持并行计算。

2 计算结果

模型在6核处理器下并行计算，耗时一天得到收敛结果。AP燃烧属于预混燃烧，因此其各项参数的变化仅存在于轴向。这里选取二维网格的目的是为以后扩散燃烧做准备。其温度在轴向的分布如图2所示。由图2可看出，模型所得到的温度分布与试验结果十分吻合，很好地模拟了AP燃烧温度的变化。

燃烧主要产物在轴向的分布如图3(a)所示，以下各图中的空心符号均代表来自Ermolin的试验数据。燃烧次要产物在轴向的分布如图3(b)、(c)所示。图3(c)中，来自Ermolin的OClO和HClO4的试验数据基本相同。因此，只用了同一空心圆来表示。

由图3(a)可见，主要燃烧产物摩尔分数的分布与试验结果只存在很小差异，而且其变化趋势和试验结果一致。图3(b)、(c)中，次要燃烧产物摩尔分数的分布与试验结果有一定偏差，但控制在一个不大范围内。同时，其变化趋势仍与试验结果保持一致。

图2 AP燃烧温度沿轴向的分布Fig.2 Temperature distribution along axis for AP combustion

图3 主要及次要燃烧产物沿轴向的摩尔分数分布Fig.3 Mole fraction distributions along the axis for main and minor combustion products

3 结论

通过涡速方程建立的AP气相燃烧详细化学动力学模型是成功的。与试验结果相比，其对主要参数的捕捉十分精准，对次要参数的捕捉有一定精度。因此，完全可用来模拟AP气相燃烧，并提供更多、更接近真实情况的数据，以供分析和研究。同时，该模型的建立为以后模拟各种预混和扩散燃烧打下了基础，特别是对固体火箭推进剂中大量采用的AP/HTPB的燃烧模拟提供了有效手段。

［1］Merrill W Beckstead，Karthik V Puduppakkam and Vigor Yang T.Modeling and simulation of combustion of solidpropellant ingredients using detailed chemical kinetics［C］//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit，2004.

［2］Ermolin N E，Korobeinichev O P，Tereshchenko A G，et al.Measurement of the concentration profiles of reacting components and temperature in an ammonium perchlorate flame［J］.Combustion，Explosion and Shock Waves，1982，Vol.18.

［3］Ermolin N E.Model for chemical reaction kinetics in perchloric acid-ammonia flames［J］.Combustion，Explosion and Shock Waves，1995，31.

［4］Balay S Buschelman，Eijkhout K V，et al.PETSc users manual，mathematics and computer science division［M］.Argonne National Laboratory，Revision 3.0.0.