固体火箭发动机喷管内气粒两相流动的CFD-DSMC模拟①

吴限德，张 斌，陈卫东，夏广庆，陈茂林

(1.哈尔滨工程大学航天与建筑工程学院，哈尔滨 150080;2.西北工业大学燃烧、流动和热结构国家级重点实验室，西安 710072;3.大连理工大学工业装备结构分析国家重点实验室航空航天学院，大连 116024)

0 引言

从20世纪后期起，美军就开始了空天项目的研究与开发，其中包括作战保障卫星系统、反导武器系统、反卫星武器、空天飞机、轨道轰炸机等。在众多的空天项目中，各类固体火箭发动机作为一种重要动力装置，扮演着重要角色。如超高声速拦截弹中采用的侧喷直接力控制技术，在美国的PAC-3、俄罗斯的S-400和欧共体的ASTER中已获得成功运用［1－3］。在许多情况下，由于从固体火箭发动机喷管喷出的高温高速颗粒的冲刷效应会给空天平台的热防护系统造成严重破坏，此时气粒两相稀薄羽流对空天平台的影响不容忽视。因此，急需开展高空环境中固体火箭发动机气粒两相流动的研究工作。

为了能更好地模拟高空环境中喷管内外的气粒两相流动，需将二者结合进行一体化计算。实现一体化计算的难点并不在于CFD方法和DSMC方法在模拟气相流动时界面处的处理，而是在于界面处颗粒相的处理。在连续流动中，颗粒相的描述通常采用“颗粒轨道模型”或“拟流体模型”［4］。

以此两种方法模拟得到界面处颗粒相的参数，很难在稀薄气粒两相流动的模拟中再现颗粒运动的随机性和真实性，同时不良的界面处理方法也会引入较大的人为误差。采用DSMC方法描述连续流中颗粒相的运动，则在界面处无需过多处理(仅需更换相互作用模型)，即可实现对其在稀薄流中的描述。

目前，国内仅有国防科大的陈伟芳［5］和黄琳［6］开展了超声速管道和气粒两相自由射流的CFD-DSMC研究，但未见对喷管这一典型的压-跨-超流动进行CFDDSMC的气粒两相模拟。文中采用CFD-DSMC方法，模拟了JPL喷管中的连续气粒两相流动，研究不同颗粒含量和颗粒粒径下气相和颗粒相的流动规律，并与“颗粒确定性轨道模型”和“拟流体模型”得到的结果进行了对比。

1 气相数值方法

1.1 控制方程

气相控制方程为不计体积力和无内热源的三维非定常N-S方程组。在笛卡尔坐标系下，其积分形式如式(1)所示。

控制方程中其余各项的物理意义和具体表达式见文献［1］。

1.2 计算方法

采用中心有限体积法求解。对流项采用中心差分格式，并添加各向异性人工粘性求解，扩散项采用中心差分格式求解，时间项采用显式四步Runge-Kutta法求解，同时采用隐式残值光顺法加速收敛，湍流粘性系数采用B-L模型求解。

1.3 边界条件

气相入口给定来流总温、总压、来流马赫数和方向角;气相出口处参数由内场按二阶外插获得;气相壁面采用绝热、无滑移固壁边界条件。

模拟工况:喷管入口处总压1.034 2 MPa，总温555.0 K，来流马赫数0.1，来流方向角0°。

2 颗粒相数值方法

2.1 气相对颗粒相作用的数学模型

颗粒相的位置、速度和温度的计算公式分别如式(2)～式(4)所示。

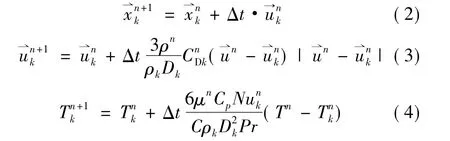
式中 下标k表示第k束颗粒;Dk为第k束颗粒的直径;为第k束颗粒的滑移速度;CDk为第k束颗粒的滞止系数;Cp和C分别为颗粒和气体的比热容;Nuk为第k束颗粒的努谢尔特数;Pr为Prandtl数。

2.2 颗粒相对气相作用源项的计算

颗粒相对气相作用源项的计算公式如式(5)所示。

式中 Vi，j，k为网格单元体积;Nk为第k束颗粒中的真实颗粒数。

2.3 边界条件

颗粒相入口给定颗粒的质量流率、温度、速度和相关物性参数(如密度、比热容)。在每个时刻步下，入口边界均有仿真颗粒进入计算区域，仿真颗粒的位置按随机方式给出。

颗粒相出口处按吸收边界处理，同时注销颗粒的编号和相应属性。

颗粒相壁面边界采用 Tabakoff［7］的经验公式，确定颗粒碰撞后的速度方向和大小。

模拟工况:颗粒的速度和温度与气相相同，颗粒密度为 4 004.62 kg/m3，颗粒比热容为 1 380 J/(kg·K)。计算中，选择的颗粒质量分数分别为0、0.10、0.30，选择的颗粒粒径分别为 1、10、20 μm。

3 计算结果与分析

JPL喷管的几何结构参见文献［7］。计算中，气相的计算区域为实体喷管的1/4，采用结构化网格计算;颗粒相的计算区域为气相计算区域的一个扇面，采用轴对称模型描述，每一时刻下对颗粒的速度和位置进行轴对称修正，并在径向对颗粒做复制-删除操作;两相耦合算法采用PSIC(Particle Source In Cell)算法，将颗粒相对气相的作用源项按位置施加给气相计算区域中的所有扇面。

3.1 气相和颗粒相参数分布规律

图1和图2给出了在颗粒质量分数0.30、颗粒粒径1 μm计算条件下，得到的喷管中气相和颗粒相的主要参数分布情况。由图1可看出，颗粒相对气相流动的阻滞作用非常明显，能显著影响气相流场中的速度和马赫数分布规律。同时，颗粒相对气相的加热作用也十分显著。

图1 气相参数分布Fig.1 Contours of gas-phase flow parameters

从图2可看出，颗粒在气相作用下加速运动，同时与气相间的传热，导致自身温度明显降低。由颗粒相浓度云图(c)可看出，壁面附近颗粒浓度最大。同时，在喷管喉部处，颗粒浓度梯度明显，且在轴线附近颗粒浓度较小。在相同工况下，由颗粒确定轨道模型计算得到的无粒子区中，仍有少量颗粒存在，且其分布具有一定的非连续性。

图2 颗粒相参数分布Fig.2 Contours of particle-phase parameters

3.2 颗粒质量分数对气相流动参数的影响

图3给出了不同颗粒质量分数下，气相在轴线上马赫数的分布。由图3可知，随颗粒质量分数的增加，气相在轴线上的马赫数逐渐降低。这是由于颗粒质量分数越高，单位体积内的颗粒数密度越大，对气相流动的阻碍作用越大。

图4给出了不同颗粒质量分数下，气相在轴线上温度的分布。由图4可知，随颗粒质量分数的增加，气相在轴线上的温度逐渐上升。这是由于颗粒质量分数越大，单位体积内颗粒对气相的热交换更为强烈，从而导致气相升温。以上结果与曾卓雄［8］采用拟流体模型获得的结果的分布趋势相同。

图3 不同颗粒质量分数下气相在轴线上的马赫数分布Fig.3 Distributions of Ma number along the axis at different concentrations of particles

3.3 颗粒粒径对气相流动参数的影响

图5和图6分别为不同颗粒直径下，气相在轴线上的马赫数和温度分布。颗粒直径越小，其表面积越大，与气相动量和能量的交换越显著。因此，随颗粒粒径的减小，气相在轴线上的马赫数逐渐降低，气相在轴线上的温度逐渐升高。

以上结果与于勇等［7］采用颗粒确定性轨道模型获得的结果分布趋势相同。

图5 不同颗粒粒径下气相在轴线上的马赫数分布Fig.5 Distributions of Ma number along the axis at different diameters of particles

图6 不同颗粒粒径下气相在轴线上的温度分布Fig.6 Distributions of temperature along the axis at different diameters of particles

4 结论

采用CFD-DSMC方法，模拟了JPL喷管中的气粒两相流动，得到了气相和颗粒相的主要参数分布规律，并研究了颗粒含量和颗粒粒径对气相流场的影响。研究表明:

(1)颗粒含量越高，对气相的减速作用越大，同时对气相的加热效应也越明显。

(2)颗粒的粒径越小，对气相的减速作用越大，同时对气相的加热效应也越明显。

(3)与采用颗粒确定性轨道模型计算得到的无粒子区对比发现，按照文中计算方法，该区域仍有少量且非连续的颗粒存在。

［1］徐敏，陈士橹.侧喷干扰流场计算及分析［J］.西北工业大学学报，2003，21(3).

［2］Roger R P.The aerodynamics of jet thruster control for supersonic/hypersonic endo-interceptors:lessons learned［R］.AIAA 1999-0804.

［3］Graham M J，Weinacht P.Numerical simulation of lateral control jets［R］.AIAA 1999-0510.

［4］方丁酉，张为华，杨涛.固体火箭发动机内弹道学［M］.长沙:国防科技大学出版社，1997.

［5］陈伟芳，常雨.三维管道超声速气固两相流动的CFD/DSMC 仿真［J］.推进技术，2005，26(3).

［6］黄琳，刘君.气-固两相自由射流的粒子仿真方法［J］.国防科技大学学报，2002，24(3).

［7］于勇，刘淑艳，张世军，等.固体火箭发动机喷管气固两相流动的数值研究［J］.航空动力学报，2009，24(4).

［8］曾卓雄.密相可压气固两相湍流流动的理论分析及其数值模拟［D］.西安:西安交通大学，2001.