具有消息恢复功能的盲签名方案
刘 媛,张秉儒
(青海师范大学,青海 西宁810000)
盲签名已经发展成为一类特殊的数字签名,签名者不知道所签消息的具体内容,接收者将盲签名进行脱盲变换转化为普通的签名,签名人即使记录每次签名的记录也不能将盲签名和脱盲后的签名相关联[1].在那些要求用户匿名性的场所,如匿名证券交易,口令认证,匿名电子现金和匿名电子投票等领域,盲签名技术发挥着重要作用.
在保证安全的前提下,密码学家们致力于尽量减少通信量研究,Nyberg-Rueppel提出了消息恢复签名方案[2],只需传递签名,接收方可以由签名和密钥恢复消息,直接缩短了传递的信息量,节省通信带宽,提高效率.
当前的签名方案多数是由一个安全的杂凑函数将消息m对应到h(m),以此保证消息的完整性、认证性和安全性.且h(m)的长度远小于m的长度.这样一来恢复的是h(m)而不是m;若在签名方案中用m,消息的保密性势必会受到威胁.冗余函数可以兼顾保密性和消息恢复特性,不过冗余函数的运算效率要低于 hash函数,因此其更适用于短消息传递.
签名技术发展到现在,对签名者的不可否认性进行了较为深入的研究,提出了各种签名者不可否认的方案.基于当前的网络技术,信息传送过程中的延迟或者丢失是客观存在的,如果接收方恢复了消息却予以否认,这样的纠纷必须通过监管和技术两方双管齐下予以解决.为了满足当今社会的需求,对收发双发不可否认的签名技术的研究至关重要.
笔者在已有研究基础上做了进一步尝试,结合公钥/私钥密码体制,提出一个收发双方都不能否认的具有消息恢复特性的盲签名方案,有效地解决了上述问题,具有很好的实用价值和应用前景.
1 冗余函数
2 具有消息恢复功能的双方不可否认盲签名协议
2.1 系统初始化
2.2 生成可恢复消息的盲签名
生成可恢复消息的盲签名步骤:
步骤1 签名人随机选择 k∈Zq,计算 r=gkmod p.
步骤2 将r发给消息拥有者;消息拥有者将消息进行冗余变换 m→R(m),随机选取 l1,l2,l3∈Zn,盲化R(m):

步骤3 将r'发送给签名人,签名人不知道R(m),计算s=r'x+k mod q,然后将s发给消息拥有者.消息拥有者验证gs=yr'r mod p是否成立.若成立,计算S=sl1+l2mod q,(R,S)为常规的具有消息恢复性能的的盲签名;否则输出“false”.任何人都可以验证签名的正确性:R(m)=g-SyRR mod p.再由公开的冗余函数恢复原消息.通常只希望指定的接收者能够恢复消息,将(R,S)处理得到一个指定接收者的签名[4].
2.3 (R,S)变换为指定接收者的盲签名
(R,S)变换为指定接收者的盲签名步骤:
步骤1 签名拥有者(以下称为A)随机选取对称密钥k,计算 M=Ek(R,S),与关键字ξ结合后签名并加密,发送m1给指定的接收人(以下称为B):

式中:ξ为关键字,包含报头,消息摘要等;ωn为实时时间戳,n=1,2,3,…,N;D 和 E 为 RSA 的加密/解密算法;PA,SA分别为A的公钥和私钥;PB,SB分别为B的公钥和私钥.
步骤2 B收到m1后,计算得到ξ和M,根据ξ中的内容判断是否继续通信过程.若不需要该报文,单方面终止通信,否则计算

步骤3 发送m2给A,A保留m2作为B收到m1的证据,将k签名加密得到的-k发送给B:

步骤4B解密-k得到T″,判断时间戳ω3是否合理且没有使用过,保存ω3,计算:

这样就可以验证签名的正确性,计算得到R(m),再利用R-1得到m.
3 对上述方案的进一步改进
上述方案中,B仍然可以通过否认最后一步曾经收到-k,来达到对自己有利但违背公平公正原则的目的.为此引入可信第三方CA来制衡.A选取a∈,传送λ =(,IDB,IDA)给B.B 选择随机数b∈,传送 μ =,gb,IDA,IDB)给 A,H 是收到 λ的反馈承诺.A收到μ以后,计算
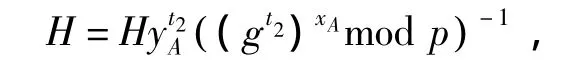
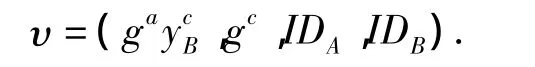
传送υ给CA,并通知B从CA处获得新数据.B通过与CA的身份认证得到υ,计算

B用消息密钥k解密

恢复R(m),检验如果R(m)∈R(M),则m=R-1(R(m));如果这个消息m有意义,并且和关键字ξ中的信息吻合,就认为这个消息是安全、可靠、有效的[5-6].
4 安全性分析
1)收方不能否认其收到签名.B首先收到的是加密后的签名,没有得到 ga之前,既不能对签名进行验证,也不能得到冗余消息R(m),他必须向A发送已经接收到签名的证据H,A才会将ga传送给B,而有关ga的数据A必须经由CA得到.这样,由于可信第三方的存在,B不能否认他收到-k,若出现了上述问题中的纠纷,只能由他自己承担责任.从而维护了信息交互过程的公平公正性,有利于进一步促进该类协议的发展,增强人们对密码学协议的信心,更好地服务人们的生活.
2)原始签名的不可伪造性.任何人要伪造一对有效的盲签名,使得

成立,有以下3种途径:①任取R,S,带入上式中,R(m)=g-SyRR mod p,这样得到的 R(m)冗余度非常高,逆函数得到的消息没有错误且有意义的概率小之又小,也就是说冗余函数的引进有效防止了恶意的伪造攻击;②任取消息m和R,从中解出S,等价于求解离散对数问题;③任取消息m和S,从中解出R,比求解离散对数问题还要困难.
3)签名者的不可否认性.签名中含有A的私钥,B在验证时用到A的公钥,A不能否认自己的签名.
4)CA不能冒充A,也不能验证签名.RSA算法保证了B可以确信消息来源和恢复消息,其他人要想求得A的私钥,面临求解离散对数难题.由于A将gα以加密的形式传送给TTP,在没有B的私钥的情况下,很难获得gα;即便是不幸CA知道了gα,但没有B的私钥,还是不能验证签名并恢复消息.这就有了双重的安全保障。
5)签名只能被指定的接收方验证恢复.RSA算法中含有接收方的公钥,只有知道接收方的私钥才能验证并恢复消息,故可以认为签名(R,S)只能被指定接收方验证并恢复消息.
6)盲性分析.可以证明这是一个强盲签名方案.签名人的视图为(r,r',s),指定的接收方视图为(R,S,M),他们关系如下:

任给一组(r,r',s)和 (R',S',M'),任选 l1,那么
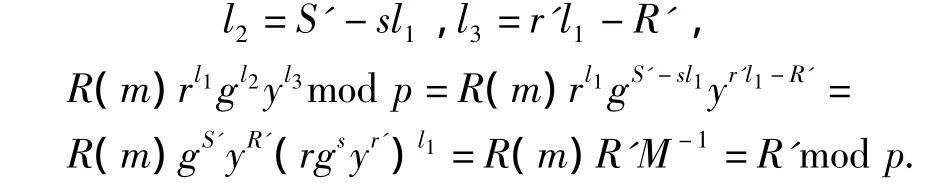
因此(r,r',s)与任意一组(R',S',M'),都存在一组l1,l2,l3与之对应,这个方案是无条件盲的.
5 结语
数字签名的作用之一是防止抵赖,已有的方案对签名人做了这方面的限制,但是对接收方行为的规范性研究较少.针对这个问题,在具有消息恢复功能的签名方案的基础上,提出了一种收方不可否认的方案.该方案过程简单明了,为构造更简洁实用的协议做了一些探索,多次信息交互所花费的时间和带宽,避免了上述漏洞引起的纠纷,彻底保证了通信的公平公正性.保密性好,特别适合于商业领域的信息交互.需要指出的是,最后一步的传递必须要通过可信第三方,而现实中完全诚实可靠的第三方是个较难实现的问题,在较大的系统中,可信第三方也会成为系统的瓶颈.
同一对消息签名,有的时候需要发送给不同的接收者,如果采用指定接收人的方案,对于每一个接收者,都要重新进行签名,这无疑是种浪费.方案中每一个消息(冗余消息)都只对应着一个原始的签名,用RSA密码算法,对不同的接收者使用不同的公钥加密,就可以发送给不同的接收者,只保证有指定的接收者能够验证并恢复消息.
[1]赵泽茂.数字签名理论[M].北京:科学出版社,2007.
[2] Nyberg K,Rueppel R.Message recovery for signature schemes based on the discrete logarithm[J].Designs,Codes and Crytography,1996,7(1 -2):61 -81.
[3]吴佩萱.引入冗余函数的基于椭圆曲线的消息恢复签名方案[J].长江大学学报,2005,2(10):351 -225.
[4]屈娟,张建中.具有消息恢复的指定接收者的代理盲签名方案[J].计算机工程与应用,2008,44(33):110-111.
[5]黄振杰,王育民,陈克非.Nyberg-Rueppel消息恢复盲签名的一般化和改进[J].通信学报,2005(12):131-135.
[6]赵泽茂,吴高远,刘凤玉.基于椭圆曲线的具有消息恢复的签名方案[J].计算机工程与科学,2005(2):3-4.

