缩进式Gurney襟翼对风力机流动控制的数值研究

赵万里，张利达

(华北水利水电学院，河南郑州450011)

流动控制技术是目前空气动力学研究的重要方向，以Gurney襟翼为代表的流动控制技术在大型飞机的流动控制中得到了快速发展和广泛应用［1－5］.关于Gurney襟翼在风力机中的应用，国外从20世纪末开始研究，并取得了一定的成果.文献［6－10］对在传统翼型NACA0015，NACA0020以及风力机专用翼型NREL S809上加装不同高度的正常式Gurney襟翼进行了试验研究，证实了Gurney襟翼在减少风力机叶片分离、提高效率方面具有明显的效果.

国内近几年才开始研究Gurney襟翼在风力机中的应用.文献［11］对大型风力机专用翼型FFAW3-211加装正常式Gurney襟翼后进行了数值模拟研究，验证了正常式Gurney襟翼能够有效提高风力机气动性能，获得了襟翼高度对风力机气动性能的影响规律，并得出最佳襟翼高度为(1% ～2%)c.文献［12］通过风洞模型实验，在垂直轴风力机叶片尾缘加装不同高度的正常式Gurney襟翼，通过测量风力机功率发现:在垂直轴风力机叶片尾缘加装Gurney襟翼能够提高风力机发电功率，并探讨了Gurney襟翼控制风力机性能的流动机理.

作者对大厚度、低雷诺数风力机专用翼型FFA－W3－211加装缩进式Gurney襟翼后进行了数值研究，探讨缩进式Gurney襟翼对风力机专用翼型气动性能的影响规律，并研究了最佳襟翼位置.

1 物理模型及数值方法

文献［2，5］的实验结果表明，加装Gurney襟翼后只对厚翼型或大后缘角的翼型可在全部攻角范围内提高其升阻比.这里采用大厚度、低雷诺数的FFA－W3－241翼型，相对厚度 24.1%，相对弯度2.2%，弦长 c=2.2 m，雷诺数 Re=1.5 ×106，来流速度 v=10 m/s.使用 FLUENT6.3.26 求解器，控制方程选为质量加权平均的N－S方程和低雷诺数SST k－ω湍流模型［12］.

1.1 低雷诺数SST k－ω湍流模型

SST k－ω模型用一个混合函数将k－ω和k－ε模型融合.在近壁区域使用k－ω模型，使计算更加稳定精确;在远场区域转变为k－ε模型.湍动能k和比耗散率ω的输运方程为:

设参数 φ(包括 σk，σω，β，β*，γ)的值是两组参数值的混合，

应用于边界层计算的常数φ1为:

应用于远壁区域计算的常数φ2为:

混合函数F1定义为:

涡黏性系数为:

1.2 计算网格

使用结构网格剖分计算区域，干净翼型网格数量18.7万，带 Gurney襟翼的网格数量39.1万.计算域的网格前为30倍弦长，后为40倍弦长，上下各为30倍弦长，第1层网格尺寸1×10－5.计算网格划分、整体网格以及局部网格分布如图1所示.

图1 计算网格及其分布

1.3 边界条件

计算域上、左和下边界均采用速度入口边界条件，计算域右边界采用压力出口边界条件，翼型以及缩进式襟翼作为无滑移壁面边界条件处理.

1.4 求解方法

采用有限体积法离散控制方程，对流项采用二阶迎风格式，扩散项采用中心差分格式，压力速度耦合采用基于压力的耦合算法处理，离散代数方程组采用 Gauss－Seidel迭代法求解［12］.

2 计算结果分析

2.1 襟翼高度对翼型升、阻特性的影响

相同襟翼高度、不同襟翼位置对应的升力系数随来流攻角的变化曲线如图2所示.从图2可以看出，缩进式Gurney襟翼同样会带来升力系数的增加，但升力线斜率几乎没有变化;失速攻角以后，大多数襟翼仍然具有较高的升力系数.这种升力的增加主要是由于Gurney襟翼增大了翼型的有效弯度，使上下翼面压差增大，从而提高升力.不难看出，加装Gurney襟翼与不加装Gurney襟翼的翼型处于同一攻角时，前者的有效攻角大于后者，因而升力较后者有所提高.这一结果与文献［3］吻合较好.从图2还可以看出，加装缩进式Gurney襟翼后，改变了翼型尾缘附近绕流，可以增大失速攻角.

图2 不同襟翼位置下Cl随AOA的变化曲线

襟翼高度为2%c(c为弦长)对应情况下(图2中g－2)的翼型升力系数明显大于襟翼高度为1%c对应情况下(图2中g－1)的翼型升力系数.在襟翼高度为2%c时，襟翼位置远离翼型尾缘，对应的升力系数反而下降，襟翼位置p=2%c时(对应图2中g－2－p－2)翼型的升力系数达到最大值.

相同襟翼高度、不同襟翼位置时，翼型升阻比随攻角的变化曲线如图3所示.从图3可以看出，实验与计算结果(干净翼型)的升阻比吻合较好;随着襟翼高度的增加，翼型的升阻比也相应增加;随着襟翼位置远离翼型尾缘，翼型升阻比反而下降.从图3还可以看出，加装Gurney襟翼后，翼型升阻比均大于干净翼型的升阻比.这主要是因为在干净翼型尾缘处增加了Gurney襟翼，能够有效增加翼型升力，但随着襟翼位置远离翼型尾缘，翼型阻力系数也逐渐增加，导致升阻比反而下降.结合升、阻力特性可知，最佳襟翼位置为p=2%c(图3中对应为g－2－p－2).

相同襟翼高度、不同襟翼位置时，翼型俯仰力矩系数随攻角的变化曲线如图4所示.从图4可以看出，当增加襟翼高度时，翼型低头力矩增加，且襟翼高度越大低头力矩增加越多，这再次说明Gurney襟翼使得翼型的弯度增加了［3］.

图3 相同襟翼高度、不同襟翼位置下Cl/Cd随AOA的变化曲线

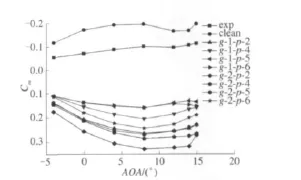
图4 相同襟翼高度下、不同翼型位置Cm随攻角AOA的变化曲线

2.2 Gurney襟翼位置对翼型流场特性的影响

2.2.1 相同攻角、不同襟翼位置下翼型流场

攻角AOA=0°，不同襟翼位置下翼型尾缘处局部的流场如图5所示.从图5可以看出，在来流攻角AOA=0°时，襟翼前方存在一个逆向分离区，在襟翼后方存在2个反向的涡，并且襟翼和尾缘处形成一个细长的尾流区;襟翼前方逆向分离区的漩涡范围随着襟翼高度的增加而增加，而襟翼后方尾流区的范围均随着襟翼离开尾缘的距离的增加而增加.

来流攻角AOA=14°，不同襟翼高度下翼型整体流场如图6所示.

由图6可知，与干净翼型相比，随着襟翼远离翼型尾缘距离的增加，翼型上翼面尾缘分离区面积先减少后增加，并且襟翼后方的尾流区范围也相应增加.这主要是当襟翼距离尾缘不远时，由于襟翼的存在，使得翼型上翼面前缘处的流速增加，在向下游流动的过程中，增大了边界层内的速度，提高了边界层抵抗逆压梯度的能力，因此使分离泡面积减小甚至消失.然而襟翼后方尾流区内2个反向涡随着来流攻角的增加，在攻角AOA=12°时，2个反向涡中的下方涡开始破碎，随着攻角的进一步增加，最终达到完全破碎.在襟翼高度很大的情况下，2个反向涡的下方涡会在尾流区内形成更大的漩涡结构，使得尾流区范围增加，进而导致整个翼型阻力增加.

2.2.2 相同襟翼高度和位置在不同攻角下翼型流场

襟翼高度h=1%c，襟翼位置p=4%c，不同来流攻角AOA下翼型流线如图7所示.从图7可以看出，随着来流攻角的增加，翼型上翼面靠近尾缘处开始出现分离泡，并且随着攻角进一步增加，分离泡的范围越来越大.但是与干净翼型相比，安装Gurney襟翼后翼型上翼面出现分离泡时的攻角AOA明显增加，即在相同来流攻角下，安装Gurney襟翼使得上翼面分离区面积减少，翼型阻力降低.另外，当AOA＞14°以后，襟翼后方的尾流区范围开始相应增加，原因和图6中尾流区范围增加的原因相同.

图7 襟翼高度h=2%c，襟翼位置p=4%c，不同AOA下翼型流线图

2.3 Gurney襟翼位置对翼型表面压力分布影响

2.3.1 相同襟翼高度和位置、不同角度下的压力分布

襟翼高度h=1%c，襟翼位置p=2%c时，翼型压力系数Cp沿弦长方向的分布随攻角的变化曲线如图8所示.由图8可知，在相同的襟翼高度和位置下，翼型上翼面吸力和下翼面压力分布随来流攻角变化明显.随着来流攻角的增加，翼型下翼面压力逐渐增加;翼型上翼面吸力逐渐增加，当来流攻角AOA=15°时，翼型上翼面吸力开始下降，翼型中部压力明显降低，这是因为在AOA=15°时翼型发生了失速，使翼型气动性能明显下降.

襟翼高度h=1%c，襟翼位置p=2%c，不同来流攻角下翼型压力等值线如图9所示.

图8 h=1%c，p=2%c，不同AOA下Cp分布曲线

图9 襟翼高度h=1%c，襟翼位置p=2%c，不同来流攻角AOA下压力等值线图

由图9可知，随着来流攻角的增加，驻点从前缘向翼型下表面移动，翼型上表面负压区明显增加，上表面前缘吸力增加，翼型下表面压力也逐渐增加，进而使得翼型升力系数随着攻角的增加而增加.

2.3.2 相同来流角度，不同襟翼位置的压力分布

AOA=14°，襟翼角度h=1%c，不同襟翼位置下翼型压力系数Cp的分布如图10所示.由图10可知，随着襟翼位置远离翼型尾缘，翼型上翼面吸力逐渐降低，下翼面的压力也逐渐减小，因此会使翼型的总的升力系数减小.

来流攻角AOA=12°，干净翼型以及不同襟翼位置下翼型压力分布等值线如图11所示.由图11可知，与干净翼型的压力分布相比，随着襟翼位置远离翼型尾缘，翼型上翼面负压区先增加而后减小，因而翼型的总升力先增加后降低，当襟翼位置p=2%c时，翼型上翼面负压区范围最大.

图10 AOA=14°，襟翼高度 h=1%c，不同襟翼位置的Cp分布

图11 AOA=12°，h=2%c，不同襟翼位置下翼型压力等值线图

3 Gurney襟翼控制流动的机理探讨

由于襟翼的存在增加了尾缘的曲率，导致翼型吸力面尾缘附近的流线向下弯曲，增大了翼型的弯度，增加了典型的环量，使升力增大.由于襟翼很小，位于边界层之内，因此它不能当作突起物.受黏性的作用，使襟翼之后形成了稳定的分离泡.该分离泡对翼型后的尾流有一个压缩作用，使尾流区变小，进而使阻力变小.

由于Gurney襟翼的存在，上翼面前缘附近吸力增加，气流流经翼型上翼面速度增加，气流在向下游流动时，将提高边界层抵抗逆压梯度的能力，进而尾缘分离区面积减少甚至消失.当襟翼位置增加到一定情况时，在一定大攻角范围内，襟翼后两个旋转方向相反的旋涡形成的分离泡下面的那一个会发生破裂，随着攻角的进一步增加，这个破裂的分离泡会在下游重新生成一个更大的漩涡结构，使得分离区面积增加，进而导致翼型阻力增加.

4 结语

对风力机专用的大厚度、低雷诺数翼型加装缩进式Gurney襟翼进行了数值模拟.研究发现，缩进式Gurney襟翼能够有效控制翼型的气动性能;加装缩进式Gurney襟翼能够提高翼型的最大升力，在合适的襟翼位置下能够降低翼型阻力，提高翼型的升阻比，进而提高风力机的气动性能.研究结果可为实际风力机的流动控制提供理论指导和技术支撑.

［1］ Mohamed Gad-EL-Hak.Flow Control:Passive，Active，and Reactive Flow Management［M］.United Kingdom:Cambridge University Press，2000.

［2］ Liebeck R H.Design of subsonic airfoils for high lift［J］.Journal of Aircraft，1978，15(9):547 －561.

［3］ Newhart D H，Pendergraft O C.A water tunnel study of gurney flaps［J］.NASA-TM-4071，1988.

［4］ Jang C S，Ross J C，Cummings R M.Numerical investigation of an airfoil with a Gurney flap［J］.Aircraft Design，1992，1(2):75 －88.

［5］ Myose R，Heron I，Papadakis M.The effect of Gurney on three-dimensional wings with and without taper，Sae technical paper 65514［R］.AIAA-96-0059，1996.

［6］ Kentfield J A C，Clavelle E J.The flow physics of the Gurney flaps devices for improving turbine blade performance［J］.Wind Engineering，1993，17(1):24 －34.

［7］ Kentfield J A C.Influence of free-stream turbine intensity on the performance of Gurney-flap equipment wind-turbines blades［J］.Wind Engineering，1996，20(2):93 －106.

［8］ Kentfield J A C.Theoretically and experimentally obtained performances of Gurney flap equipped wind turbines［J］.Wind Engineering，1994，18(2):63 －74.

［9］ Bloy A W，Durant M T.Aerodynamic characteristic of an aerofoil with small trailing edge flaps［J］.Wind Engineering，1995，19(3):167 －172.

［10］ Bloy A W，Harrison D F.Free-stream turbulence effect on Gurney-type flaps［J］.Wind Engineering，1998，22(3):149－158.

［11］赵万里，刘沛清，朱建勇，等.Gurney襟翼对风力机流动控制的数值研究［J］.电网与清洁能源，2011，27(9):85－92.

［12］赵万里.大型风力机气动设计与流动控制技术研究［R］.北京:北京航空航天大学，2011.