磁耦合调谐质量阻尼器的减振效果研究

李晓华，王宝基

(河南理工大学物理化学学院，河南焦作454000)

调谐质量阻尼器(Tuned Mass Damper，TMD)是目前高层建筑和高耸结构振动控制中应用最早的结构被动控制装置之一.目前，许多被动控制器成功地装置在世界各地的高耸建筑物和塔上.如美国纽约的Citicorp中心，波士顿的John Hancock塔，澳大利亚悉尼Centerpoint塔等.TMD系统是由弹簧、阻尼器和质量块组成的振动系统，如图1所示.

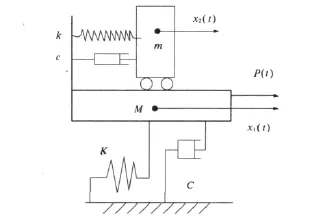
图1 TMD－结构力学模型

它对结构进行振动控制的机理是:结构在外部激励力作用下产生振动时，带动TMD系统一起振动，TMD系统相对运动产生的惯性力反作用到结构上调谐这个惯性力，使其对结构的振动产生抑制作用，达到减小结构振动反应的目的.TMD结构的应用思想最早来源于1909年Frahm研制的动力吸振器.在TMD不受约束的情况下运动，使得主结构的幅值频率得到突出的抑制［1－5］.但是，在实际工程中，当建筑物的距离或空间不能满足TMD的自由运动，TMD和墙或建筑物之间将产生碰撞.文献［6］研究了塑性碰撞TMD的参数优化，结果表明，在合理参数下能达到好的减振效果.闫安志等人［7］研究低速冲击下TMD冲击参数的敏感性.当TMD的自由运动空间有限时，虽通过参数优化也能达到较好的减振效果，但碰撞会产生噪声并减少主体结构的寿命.

通过改变系统的阻尼方式，在保证主体结构的减振效果的同时，减小TMD和主结构相对运动的位移，从而使TMD能够自由运动.避免碰撞引起的不必要的危害，为未来的高耸结构的减振提供有价值的理论参考.

1 模型和运动方程

为了便于分析有磁耦合的调谐质量阻尼器的动力学特性，建立了3个自由度的力学模型，如图2所示.模型通过磁耦合把电学部分和机械部分构成一个整体.因此，这2部分的耦合是通过永久磁铁引起的安培力来确保的，永久磁铁在机械部分产生一个安培力，同时在电学部分产生一个感应电动势.电学部分由电阻R、电感L和电容C组成;机械部分由质量m1，与受余弦P(t)=P0cos(Ωt+φ)激励的振荡器相连，质量m2放在质量m1上，质量m2通过一个刚度系数为k1的弹簧与质量m1相连.电学部分的作用是:当主体结构受到简谐激励P0cos(Ωτ)时，主体结构和TMD之间发生相对运动，带动线圈在磁场中切割磁力线，产生感应电动势，使机械部分增加一个安培力来阻碍二者之间的相对运动，从而减小和抑制机械振动的振幅.用基尔霍夫定律和牛顿定律，考虑安培力和感应电压的贡献，系统的微分方程为

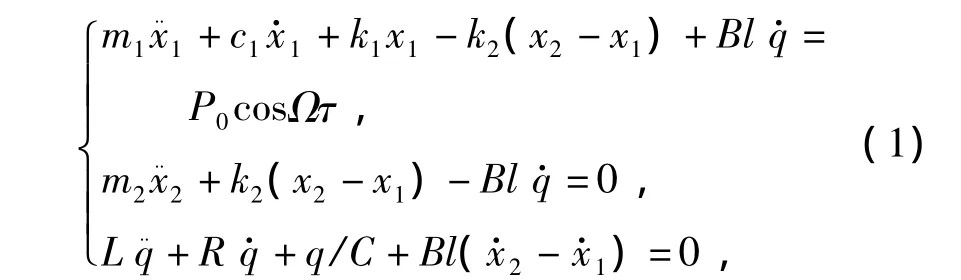
式中:x1，x2分别为主结构和TMD的位移;q为电容器极板上的瞬时电荷电量;变量上的“·”表示对时间求导;m1，m2分别为主结构和TMD的质量;k1，k2分别为主结构和TMD的刚度;l为磁场→─Bm中线圈的有效长度;L，R，C分别为线圈的电感、电阻和电容器的电容;P0cos(Ωτ)为系统受到的谐激励.

图2 有磁耦合的TMD结构力学模型

为了便于分析动力学特性和对参数进行研究，这里采用无量纲化，设无量纲变量为

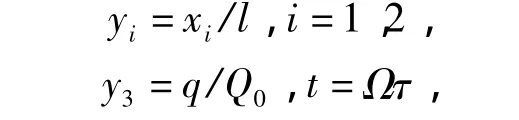
式中Q0为电容器的参考电荷电量.

将上面的无量纲变量代入式(1)，化简为

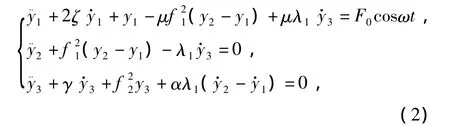
无量纲变量为:

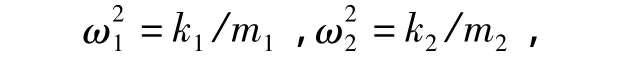
式(2)中:变量上的“·”表示对时间的求导;y1，y2分别为主体的位移和TMD的位移;y3为电容器的瞬时电荷;ζ，γ分别为主结构和电系统的阻尼比;λ1，α分别为耦合参数和正系数;β为非线性系数;f1，f2，ω分别为TMD、振荡电路和外激励的固有频率与主结构的固有频率的比值;F0为外激励的无量纲幅值;t为无量纲时间.

2 数值计算

2.1 参数优化

由于系统中的参数比较多，为了研究某一参数的影响，需先固定其它参数不变.设参数ζ=0.02，μ=0.02，γ =1，f1=1，f2=1，E0=0.5 不变，研究耦合参数λ1和耦合参数比α对系统减振效果的影响.对不同的耦合参数λ1和耦合参数比α进行数值计算，结果见表1.表1中Am，Bm分别表示主结构和TMD的稳态响应幅值的最大值.

表1 主结构和TMD的最大幅值表

从表1中很容易看出，当α=2.0和λ1=0.75时，TMD的所需的运动空间较小，但主结构减振效果就比较差;而当α=0.5和λ1=0.75时，不但主结构有很好的减振效果，而且TMD的所需的运动空间也相对较小.故现取耦合参数比α=0.5，耦合参数λ1=0.75，其它无量纲参数 ζ=0.02，μ =0.02，f1=1，f2=1，E0=0.5，γ 分别取 0.5，1.0，1.5，2.0 来研究主结构和TMD的频响曲线，结果如图3和图4所示.由图3和图4可知，要想保证主结构有好的减振效果，同时又使TMD的自由运动空间相对较小，γ=1.5是比较合适的参数.

综上所述，磁耦合TMD的耦合参数α=0.5，λ1=0.75，γ =1.5 为系统的相对较优参数.

2.2 有磁耦合的TMD和TMD的减振效果的比较

下面对磁耦合的TMD和普通TMD的减振效果的比较.虽与参考文献［8］中的无量纲标准不同，但各个参数的表达式除F0以外均相同，并且最佳参数的选取与F0无关，因此，这里仍可采用参考文献［8］中的最佳频率比和阻尼比的设计，参数之间的关系见式(3).

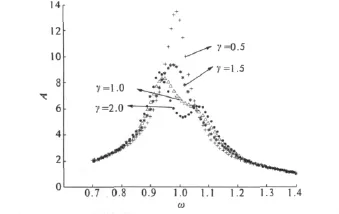
图3 不同γ下磁耦合TMD主结构的频响曲线

图4 不同γ下磁耦合TMD的TMD频响曲线

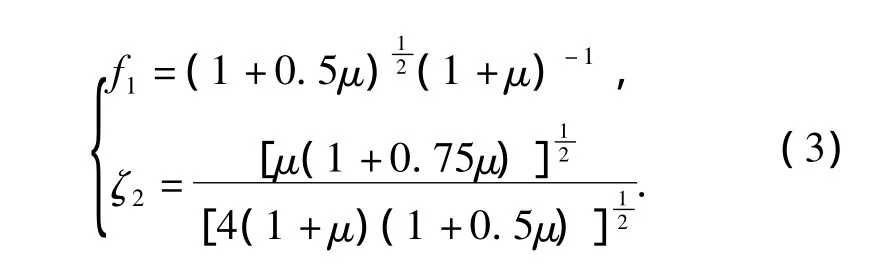
下面讨论在主结构、质量比和外激励相同的条件下，使TMD采用最佳频率比和阻尼比，其无量纲参数 ζ=0.02，μ =0.02，f1=0.98，E0=0.5，ζ1=0.005.有磁耦合的TMD采用文中研究的相对较优的耦合参数，其无量纲参数为 ζ=0.02，μ =0.02，λ1=0.75，α =0.5，γ =1.5，f1=1，f2=1，E0=0.5，来比较二者对主结构的减振效果，以及TMD相对于主结构的自由运动空间.有磁耦合TMD和普通TMD二者稳态时主结构和TMD的幅频特性曲线分别如图5和图6所示.

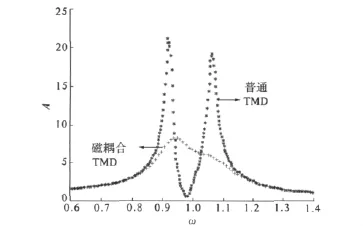
图5 磁耦合TMD和普通TMD的主结构的频响曲线

由图5和图6可以看出，虽然普通TMD在外激励频率 ω∈［0.94，1.03］时，处于反共振阶段，使得普通TMD优于磁耦合TMD，但此时有磁耦合的TMD的减振效果也比较好.从主结构的减振方面看，稳态时，磁耦合TMD的位移最大幅值为8，而普通TMD位移最大幅值为22.从TMD相对于主结构的运动空间来看，随着外激励频率的变化，TMD稳态时位移的最大幅值达到了180，而磁耦合TMD稳态时位移的最大幅值只有40.由此可见，在减振过程中，从主结构的减震效果和TMD所需的运动空间来看，磁耦合TMD远远小于普通TMD，可在很大程度上避免碰撞的发生，使人们的生活更舒适，并提高主结构的寿命和鲁棒性.

图6 磁耦合TMD和普通TMD的TMD的频响曲线

3 结语

建立了磁耦合TMD的力学模型，通过数值模拟对磁耦合TMD参数进行了优化，并将参数优化条件与普通TMD的减振效果进行了对比发现，在简谐激励下磁耦合TMD不但使主结构的减振效果得到了很好的提高，同时TMD的自由运动空间也获得大大节省，从而解决了TMD自由运动空间受限的问题.

［1］周定松，肖克艰.超高层建筑TMD风振控制实用设计方法［J］.建筑结构，2010，40(9):96 －99.

［2］ Benedikt Weber，Glauco Feltrin.Assessment of long-term behavior of tuned mass dampers by system identification［J］.Engineering Structures，2010，32(11):3670 － 3682.

［3］ Wang Min，Zan Tao，Yang Yi-qing，et al.Design and implementation of nonlinear TMD for chatter suppression:an application in turning processes［J］.International Journal of Machine Tools ＆ Manufacture，2010，50(5):474 －479.

［4］ Chunxiang Li，Weilian Qu.Evaluation of elastically linked dashpot based active multiple tuned mass damper for structures under ground acceleration［J］.Engineering Structures，2004，26(14):2149 －2160.

［5］唐易，顾明.某超高层建筑TMD风振控制分析［J］.振动与冲击，2006，25(2):16 －19.

［6］李晓华，闫安志.基于塑性碰撞的调谐质量阻尼器的减震效果的研究［J］.河南理工大学报，2009，28(3):340－346.

［7］闫安志，李晓华.低速冲击下TMD冲击参数的敏感性［C］∥第九届全国冲击动力学学术会议论文集.焦作:出版社不祥，2009，8:693 －698.

［8］ Warburton G B.Optimum absorber parameters for various combinations of response and excitation parameters［J］.Earthquake Engineering and Structural Dynamics，1982，10(3):381－401.