一类具有垂直传染和密度制约的SIS模型的性态分析

王彩霞，王战伟

(1.华北水利水电学院，河南郑州450011;2.郑州航空工业管理学院，河南郑州450015)

早在1927年，Kermark和Mckendrick就利用动力学方法建立了SIR传染病模型［1］.近20年来，国际上传染病动力学研究进展迅速，国内外众多的专家学者建立了大量的传染病数学模型［2－9］，对传染病的治疗和预防起到很大的作用.

很多传染病不仅可通过接触传染，而且感染者可能通过遗传传给下一代，如肝炎、肺结核等.以往的研究主要集中在水平传染上，也就是接触传染.为了更准确地了解传染病的性态，文献［6－9］研究了一些具有垂直传染的传染病模型.在传染病的研究中密度制约是不可忽略的因素.

1 传染病模型

在考虑传染病垂直传染的基础上同时考虑密度制约得到模型:

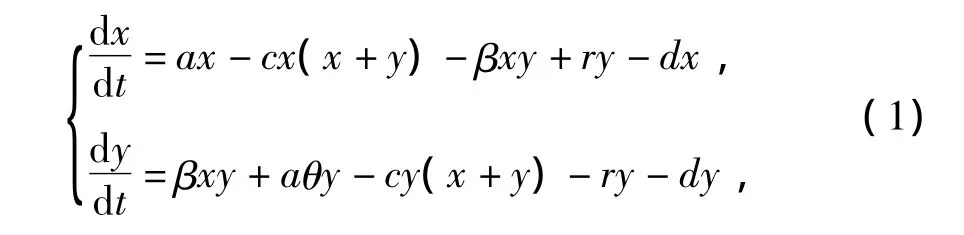
式中:x，y分别为易感者和感染者;d为死亡率;β为水平感染率;r为感染者的治愈率;ax，aθy分别为新增的易感者和感染者，0≤θ≤1反应疾病对生育能力的影响;cx(x+y)和cy(x+y)分别为易感者和感染者的密度制约项.假定所有的参数均为正，由模型的生物意义可知假定合理.

2 主要结果及证明

对于模型(1)，假设 N=x+y，有

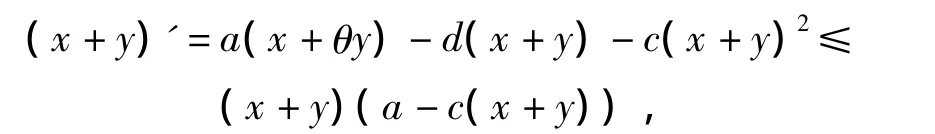
Γ ={(x，y)∈R2+:x+y ＜ －N}为模型(1)的正不变集.下面所有的分析都是在正不变集Γ内进行.

经计算可得到模型(1)的无病平衡点为E0=(0，0)，E1=(x0，0)=((a － d)c－1，0)，感染平衡点－E=(－x，－y).为了讨论平衡点的稳定性，下面给出模型(1)的雅克比矩阵

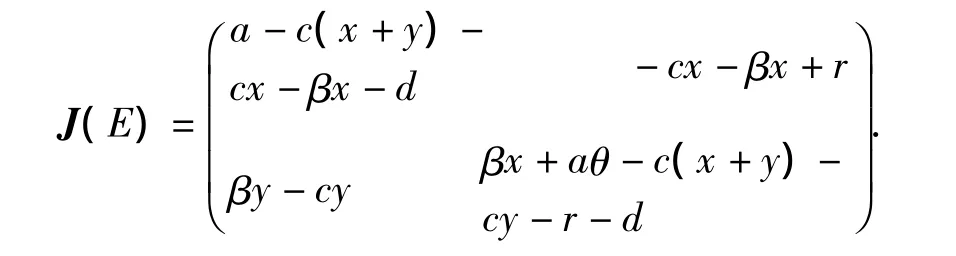
2.1 平衡点E0=(0，0)的稳定性

定理1 平衡点E0=(0，0)总是存在，并且当a ＜d时，E0=(0，0)是全局渐近稳定的.

证明平衡点E0=(0，0)的存在性由模型(1)易得.为了研究E0的稳定性，直接代入上述雅可比矩阵可得，当且仅当a＜d时，E0局部稳定.下面通过构造Lyapunov函数来证明E0的全局渐近稳定性.令

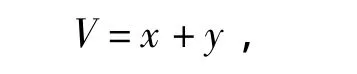
沿模型(1)的解求导计算后可得

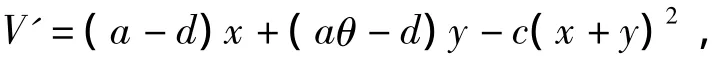
当 a ＜d 时，V'≤0，并且当且仅当(x，y)=(0，0)时V'=0.因此，利用Lyapunov-LaSalle不变原理得到当a＜d时，E0=(0，0)全局渐近稳定.

2.2 平衡点 E1=((a－d)c－1，0)的稳定性

定理2 当a＞d时，平衡点E0丢失它的稳定性，同时 E1=((a－ d)c－1，0)出现;当 R0＜1 时，无病平衡点 E1=((a－d)c－1，0)全局渐近稳定;当R0＞1时，E1是鞍点.

证明显然当a＞d时，E1存在.将E1代入雅克比矩阵整理后可得

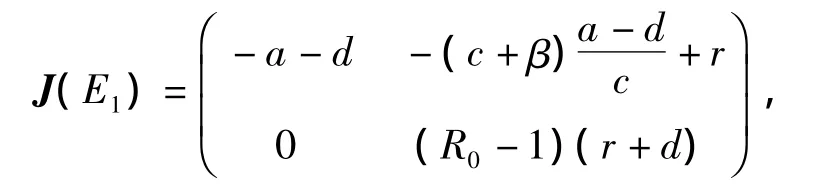
显然当R0＜1时，E1局部渐近稳定;R0＞1时，E1是鞍点.为进一步得到平衡点E1的全局性态，令

利用 Dulac 准则，构造函数 φ(x，y)=(xy)－1，由

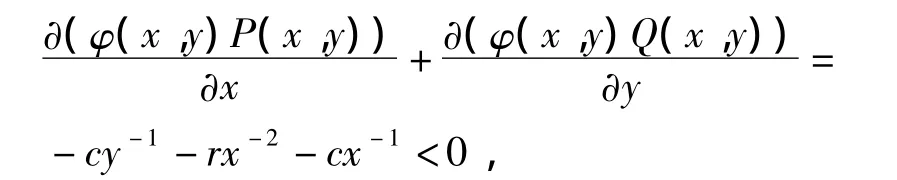
可知在正不变集 Γ内，系统(1)没有闭轨.根据Poincare-Bendixson定理可知当R0＜1时，E1全局渐近稳定.

2.3 感染平衡点－E=(－x，－y)的稳定性

由于感染平衡点的复杂性，需要先得到存在2个感染平衡点的条件.通过一般方法研究感染平衡点的稳定性非常麻烦甚至得不到结论，在这里笔者巧妙地构造了2个函数并用它们的几何特性得到了感染平衡点的局部稳定性.

令Q(x，y)=0，通过计算可以得到

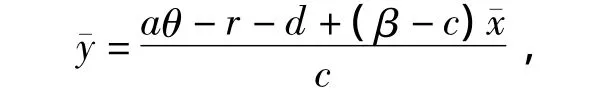
代入

可得

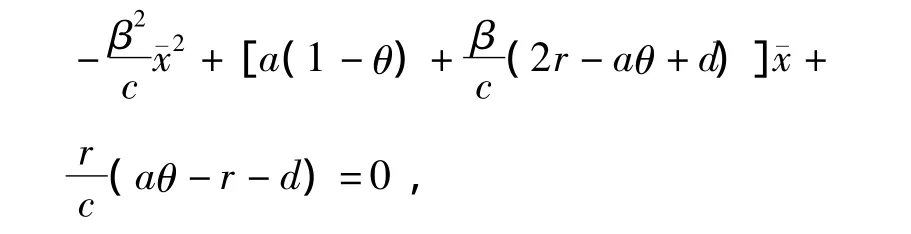
由抛物线的几何特性可知，要使方程存在2个正解必须同时满足aθ＜r+d和Δ＞0.其中，

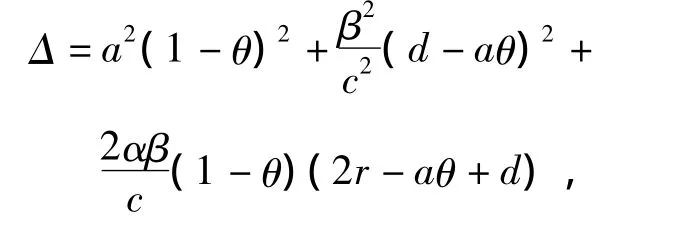
显然当aθ＜r+d时，Δ＞0一定成立.也就是说，当aθ＜r+d时，可得到2个正解分别记做－x1=x*，－x2=x*(x*＜x*)，又因为

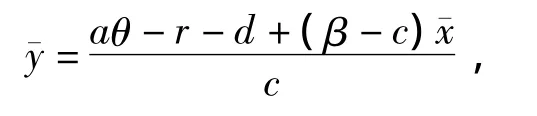
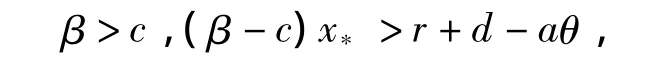
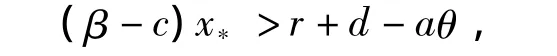
模型(1)存在2个感染平衡点 E*=(x*，y*)和E*=(x*，y*).为了研究E*和E*的稳定性，构造如下2个函数:

易知模型(1)存在2个正平衡点，等价于f1(x)和f2(x)的图形有2个正交点，对于函数f2(x)，计算后可得

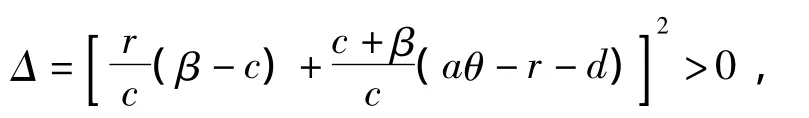
由函数的几何特性可知，当aθ＜r+d，β＞c时，2函数具有图1所示特性.

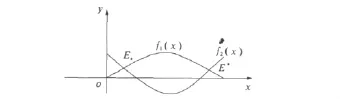
图1 函数曲线

为了得到感染平衡点的稳定性，将－E代入雅克比矩阵整理后可得

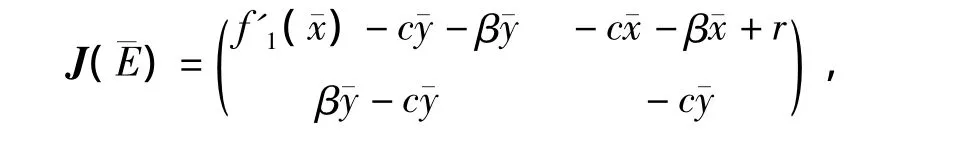
经计算可得

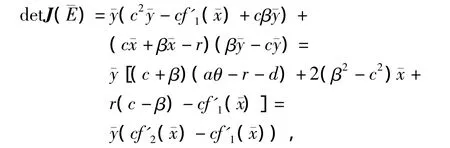
根据上述图形的几何特性，易得

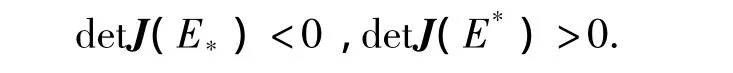
而trJ(－E)=－r－x－1－y－c－x－c－y＜0，因此，平衡点E*=(x*，y*)局部渐近稳定，E*=(x*，y*)为鞍点.进一步利用定理2中的Dulac函数，根据Poincare-Bendixson定理可知感染平衡点E*=(x*，y*)是全局渐近稳定的.(证明过程同定理2).

综上所述可得

定理3 当(β－c)x*＞r+d－aθ，β＞c，aθ＜r+d时，模型(1)存在2个感染平衡点E*=(x*，y*)和 E*=(x*，y*).并且 E*=(x*，y*)全局渐近稳定，E*=(x*，y*)为鞍点.

注定理3和定理2并不矛盾，因为条件(βc)x*＞r+d－aθ已保证R0＞1，此时E1是鞍点.

［1］ Kermack W O，Mckendrick A G.A contribution to the mathematical theory of epidemic［J］.Proc R Soc Lond，1927，A115:700 －721.

［2］马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004.

［3］ Wang Wendi.Backward bifurcation of an epidemic model with treatment［J］.Math Biosci，2006，201:58 － 71.

［4］ Wang Wendi，Ruan Shigui.Bifurcations in an epidemic model with constant removal rate of the infectives［J］.J Math Anal Appl，2004，291(2):775 －793.

［5］唐晓明，薛亚奎.具有饱和治疗函数与密度制约的SIS传染病模型的后向分支［J］.数学的实践与认识，2010，40(24):241－246.

［6］付景超，井元伟，张中华，等.具有垂直传染和连续预防接种的SIRS传染病模型的研究［J］.生物数学学报，2008，23(2):273 －278.

［7］杨建雅，张凤琴.一类具有垂直传染的SIR传染病模型［J］.生物数学学报，2006，21(3):341 －344.

［8］郭淑利，李学志.具有垂直传染的年龄结构SEIR流行病模型的稳定性［J］.应用数学学报，2005，28(4):735－751.

［9］刘开源，陈兰荪.一类具有垂直传染与脉冲免疫的SEIR传染病模型的全局分析［J］.系统科学与数学，2010，30(3):323－333.